На сегодняшний день информация играет ключевую роль, как в жизни отдельного человека, так и в бизнес-процессах предприятий. Соответственно, защита ее от искажения в системах хранения и каналах передачи данных при помощи технологии помехоустойчивого кодирования является актуальной задачей [1]. Однако, современные технологии помехоустойчивого кодирования данных [2] базируются на специализированных разделах математики, в частности, арифметике полей Галуа GF(28), и для разработки программных или аппаратных реализаций, требуются дополнительные исследования [3-8] и выведение достаточно простых для понимания, и в то же время, высокопроизводительных вычислительных схем для конкретных технологий помехоустойчивого кодирования.
Арифметика поля Галуа GF(28) с применением логарифмов в технологии помехоустойчивого кодирования на базе кодов Рида-Соломона. Поле Галуа GF(28) является частным случаем расширенных конечных полей GF(2m) характеристики 2 и имеет широкое применение в технологиях помехоустойчивой передачи и хранения информации благодаря тому, что основной единицей информации в вычислительной технике является байт. Байт состоит 8 битов и с помощью него можно представить 256 различных символов, и поле Галуа GF(28) также содержит 256 элементов, которые также можно представить в виде 8-разрядных двоичных чисел.
Яркие примеры использования арифметики поля Галуа GF(28): помехоустойчивое кодирование с применением кодов Рида-Соломона для хранения информации на оптических дисках с данными – Data CD-ROM и при передаче информации в стандарте цифрового телевещания DVB – Digital Video Broadcasting.
Поле Галуа GF(28) по определению содержит 256 элементов:
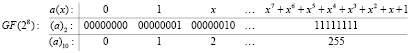
Поле Галуа GF(28), по определению являющееся полем многочленов вида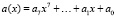 
, образуется на базе простого поля Галуа GF(2) и неприводимого многочлена 8-й степени. В технологии помехоустойчивого кодирования используется неприводимый многочлен следующего вида:
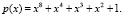(1)
В двоичном представлении неприводимый многочлен выглядит как: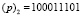 
, а в десятичном представлении: 
.
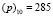В качестве примитивного элемента поля GF(28) в технологии помехоустойчивого кодирования выбирают элемент α(x) = x. При помощи него можно получить все ненулевые элементы поля. В двоичном представлении примитивный элемент поля выглядит как (α)2 = 10, а в десятичном представлении, соответственно, как (α)10 = 2.
Для формирования таблицы степеней примитивного элемента (α)10 = 2 используется представленная ниже рекуррентная схема для случая поля Галуа GF(28) с неприводимым многочленом p(x) = x8 + x4 + x3 + x + 1. Что касается таблицы логарифмов, то ее можно формировать параллельно с формированием таблицы степеней, используя десятичное представление степеней примитивного элемента в качестве индексов таблицы логарифмов.
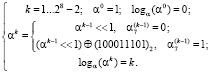(2)
Под выражением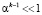 
понимается сдвиг двоичного числа влево на один разряд. Под выражением 
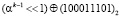понимается сдвиг двоичного числа влево на один разряд с последующей операцией «побитового» XOR результата сдвига с двоичным эквивалентом примитивного неприводимого многочлена.
Примечание. Поскольку в десятичном виде примитивный элемент поля GF(28) выглядит как (α)10 = 2, то будем также обозначать k-ую степень примитивного элемента как 2k, а логарифм от элемента a по основанию примитивного элемента как log2a.
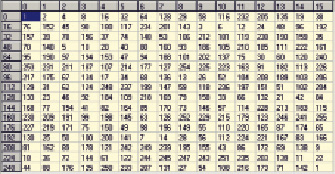
Рис. 1. Таблица степеней 2k для поля Галуа GF(28)
Ниже на рис. 1 (в виде матрицы 16 x 16) приведены степени примитивного элемента (α)10 = 2 поля GF(28), образованного при помощи примитивного неприводимого многочлена p(x) = x8 + x4 + x3 + x2 + 1. Степени примитивного элемента для компактности приведены в десятичном представлении, и расположены построчно (по 16 в строке), начиная с 0-й степени, и заканчивая 255-й. Заметим, что 255-я степень эквивалентна 0-й степени и равна 1 в силу свойств конечных полей Галуа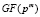 
: 
.
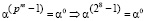Примечание 1. Для того, чтобы выбрать в таблице требуемую степень 2k, необходимо выбрать строку и столбец таким образом, чтобы сумма индексов строки и столбца (индексы строк приведены в левом заголовочном столбце серого цвета, индексы столбцов – в верхней заголовочной строке серого цвета) была равна показателю степени k.
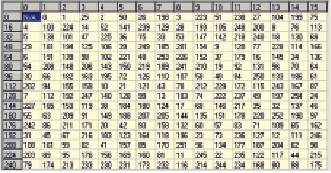
Рис. 2. Таблица логарифмов log2a для поля Галуа GF(28)
Также ниже на рис. 2 (в виде матрицы 16 x 16) приведены логарифмы по основанию примитивного элемента (α)10 = 2 поля GF(28). Логарифмы расположены построчно (по 16 в строке) для всех элементов поля, начиная с (a)10 = 0, заканчивая (a)10 = 255. Заметим, что логарифм от 0 не существует (соответствующая ячейка «N/A»).
Примечание 2. Для того, чтобы выбрать в таблице логарифм log2a заданного элемента a поля GF(28), необходимо выбрать строку и столбец таким образом, чтобы сумма индексов строки и столбца (индексы строк приведены в левом заголовочном столбце серого цвета, индексы столбцов – в верхней заголовочной строке серого цвета) была равна десятичному представлению (эквиваленту) элемента a.
Тогда с учетом всего вышесказанного имеем арифметику поля Галуа GF(28), образованного с помощью неприводимого многочлена p(x) = x8 + x4 + x3 + x2 + 1 и на базе применения логарифмов по основанию примитивного элемента (α)10 = 2:
- 
- 
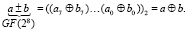
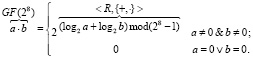(3)
- 
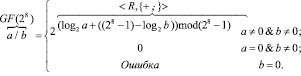
Кроме того, если необходимо найти обратный элемент по умножению, то можно воспользоваться упрощенным вариантом формулы деления элементов:
- 
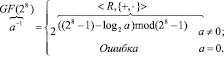. (4)
Наконец, для возведения в степень v заданного элемента a поля GF(28) можно использовать формулу, применив операцию модулярного умножения логарифмов:
- 
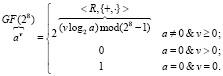(5)
Пример 1. Найдем сумму элементов расширенного поля GF(28), представленных в виде соответствующих чисел «123» и «231» в десятичной системе счисления. Имеем,
.
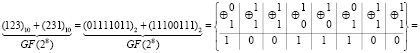
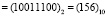Таким образом,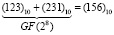 
.
Пример 2. Найдем произведение элементов поля GF(28), представленных в виде соответствующих чисел «20» и «11» в десятичной системе счисления. По таблице логарифмов для поля GF(28) имеем логарифмы элементов: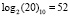 
и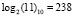 
. Тогда получаем:
.
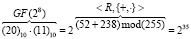По таблице степеней для поля GF(28) имеем 235 = (156)10. Таким образом:
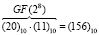
Пример 3. Найдем отношение элементов поля GF(28), представленных в виде соответствующих чисел «220» и «127» в десятичной системе счисления. По таблице логарифмов для поля GF(28) имеем логарифмы элементов: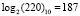 
и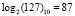 
. Тогда получаем:
.
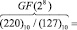
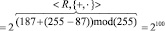По таблице степеней имеем 2100 = (17)10. Таким образом: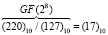 
.
Пример 4. Найдем обратный элемент по умножению для элемента «111», представленного в десятичном виде. По таблице логарифмов имеем логарифм элемента: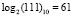 
. Тогда обратный элемент:
.
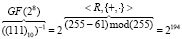По таблице степеней имеем 2194 = (50)10. Таким образом: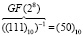 
.
Пример 5. Возведем элемент «13», представленный в десятичном виде, в заданную степень v = 17. По таблице логарифмов для поля GF(28) имеем логарифм элемента: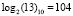 
. Тогда по формуле получаем:
.
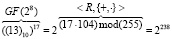По таблице степеней имеем 2238 = (11)10. Таким образом,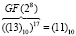 
.
Схемы прямого умножения и инвертирования элементов поля Галуа GF(28) в технологии помехоустойчивого кодирования информации. В случае необходимости высокопроизводительного прямого умножения элементов a и b поля Галуа GF(28), можно использовать заранее подготовленную свертку соответствующих многочленов a(x) и b(x) по модулю неприводимого многочлена p(x) = x8 + x4 + x3 + x2 + 1:
Аппаратную реализацию схемы умножения мы не будем приводить в силу ее громоздкости. Отметим лишь, что ее несложно построить при помощи 64 двухвходовых логических элементов «И» и 8 многовходовых сумматоров по модулю 2.
Также в случае необходимости применения высокопроизводительного вычислителя обратного элемента по умножению (для ускорения операции деления), можно использовать заранее вычисленную таблицу обратных элементов по умножению.
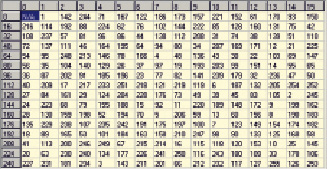
Рис. 3. Таблица обратных элементов по умножению для поля Галуа GF(28)
Ниже на рис. 3 (в виде матрицы 16 x 16) приведены обратные элементы по умножению для элементов поля Галуа GF(28), представленные в десятичном виде. Обратные элементы по умножению расположены построчно (по 16 в строке) для всех элементов поля, начиная с (a)10 = 0, заканчивая (a)10 = 255. Заметим, что обратного элемента по умножению для нуля не существует (соответствующая ячейка «N/A»).
Для аппаратной реализации таблицы можно использовать ПЗУ емкостью 256 x 8 бит.
Заключение
Таким образом, в рамках данной статьи рассмотрено поле Галуа GF(28) на базе неприводимого многочлена p(x) = x8 + x4 + x3 + x2 + 1, которое применяется в технологии помехоустойчивого кодирования информации. Также рассмотрены схема формирования таблиц степеней и логарифмов на базе примитивного элемента (α)10 = 2, формулы сложения, умножения и деления, а также инвертирования элементов и возведения в заданную степень. Приведены примеры выполнения арифметических операций с элементами поля. Также рассмотрены высокопроизводительные схемы прямого умножения и инвертирования элементов поля.
Полученные результаты могут быть использованы при разработке эффективных программных и аппаратных реализаций вычислительных блоков в рамках кодирования и декодирования информации с применением кодов Рида-Соломона.