В настоящее время информация играет ключевую роль, как в жизни отдельного человека, так и в бизнес-процессах предприятий. Соответственно, защита ее от несанкционированного доступа в системах хранения и каналах передачи данных при помощи технологии шифрования данных является достаточно актуальной задачей [1]. Однако, современные стандарты шифрования данных [2] базируются на специализированных разделах математики, в частности, арифметике поля Галуа GF(28), и для разработки программных или аппаратных реализаций, требуются дополнительные исследования [3-8] и выведение достаточно простых для понимания, и в то же время, высокопроизводительных вычислительных схем для конкретных стандартов шифрования информации.
Арифметика поля Галуа GF(28) с применением логарифмов в стандарте шифрования данных AES. Поле Галуа GF(28) является частным случаем расширенных конечных полей GF(2m) характеристики 2 и имеет широкое применение не только в помехоустойчивом кодировании информации, но и криптографии для защиты информации.
В частности, широко распространенное поле Галуа GF(28) используется в стандарте AES – Advanced Encryption Standard (усовершенствованный стандарт шифрования).
Поле Галуа GF(28) по определению содержит 256 элементов:
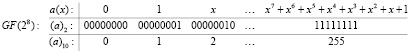
Поле Галуа GF(28), по определению являющееся полем многочленов вида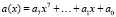 
, образуется на базе простого поля Галуа GF(2) и неприводимого многочлена 8-й степени. В стандарте шифрования AES используется неприводимый многочлен следующего вида:
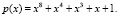(1)
В двоичном представлении неприводимый многочлен выглядит как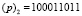 
, а в десятичном представлении: 
.
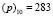Наименьшим примитивным элементом поля GF(28) является элемент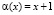 
, и при помощи него можно получить все ненулевые элементы поля, и он применяется в стандарте шифрования AES. В двоичном представлении примитивный элемент поля выглядит как (α)2 = 11, а в десятичном представлении, соответственно, как (α)10 = 3.
Для формирования таблицы степеней примитивного элемента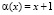 
используется представленная ниже рекуррентная схема для случая поля Галуа GF(28) с неприводимым многочленом p(x) = x8 + x4 + x3 + x + 1.
Что касается таблицы логарифмов, то ее можно формировать параллельно с формированием таблицы степеней, используя десятичное представление степеней примитивного элемента в качестве индексов таблицы логарифмов.
В двоичном представлении элементов поля операцию умножения на (α)2 = 11 в поле Галуа GF(28) можно свести к операции сдвига влево на один разряд и операции сложения («побитового» XOR), причем в случае если старший бит «предыдущей» степени был ненулевым, то еще выполняется «побитовый» XOR с двоичным эквивалентом (р)2 = 100011011 неприводимого многочлена.
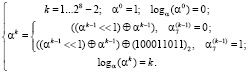(2)
Под выражением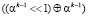 
понимается сдвиг двоичного числа влево на один разряд с последующей операцией «побитового» XOR результата сдвига с самим числом. Под выражением 
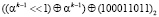понимается сдвиг двоичного числа влево на один разряд с последующей операцией «побитового» XOR результата сдвига с самим числом, с последующей операцией «побитового» XOR результата с двоичным эквивалентом неприводимого многочлена.
Примечание. Поскольку в десятичном виде примитивный элемент поля GF(28) выглядит как (α)10 = 3, то будем также обозначать k-ую степень примитивного элемента как 3k, а логарифм от элемента a по основанию примитивного элемента как log3a.
Ниже на рис. 1 (в виде матрицы 16 x 16) приведены степени примитивного элемента (α)10 = 3 поля Галуа GF(28), образованного при помощи неприводимого многочлена p(x) = x8 + x4 + x3 + x + 1. Степени примитивного элемента для компактности приведены в десятичном представлении, и расположены построчно (по 16 в строке), начиная с 0-й степени, и заканчивая 255-й.
Рис. 1. Таблица степеней 3k для поля Галуа GF(28) для AES
Примечание 1. Для того, чтобы выбрать в таблице требуемую степень 3k, необходимо выбрать строку и столбец таким образом, чтобы сумма индексов строки и столбца (индексы строк приведены в левом заголовочном столбце серого цвета, индексы столбцов – в верхней заголовочной строке серого цвета) была равна показателю степени k.
Также ниже на рис. 2 (в виде матрицы 16 x 16) приведены логарифмы по основанию примитивного элемента (α)10 = 3 поля GF(28). Логарифмы расположены построчно (по 16 в строке) для всех элементов поля, начиная с (a)10 = 0, заканчивая (a)10 = 255. Заметим, что логарифм от 0 не существует (соответствующая ячейка «N/A»).
Рис. 2. Таблица логарифмов log3a для поля Галуа GF(28)для AES
Примечание 2. Для того, чтобы выбрать в таблице логарифм log3a заданного элемента a поля GF(28), необходимо выбрать строку и столбец таким образом, чтобы сумма индексов строки и столбца (индексы строк приведены в левом заголовочном столбце серого цвета, индексы столбцов – в верхней заголовочной строке серого цвета) была равна десятичному представлению (эквиваленту) элемента a.
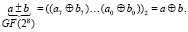
Тогда с учетом всего вышесказанного имеем арифметику поля Галуа GF(28), образованного с помощью неприводимого многочлена p(x) = x8 + x4 + x3 + x + 1 и на базе применения логарифмов по основанию примитивного элемента поля (α)10 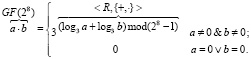= 3:
- 
- 
(3)
- 
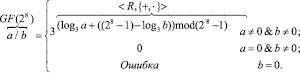
Кроме того, если необходимо найти обратный элемент по умножению, то можно воспользоваться упрощенным вариантом формулы деления элементов:
- 
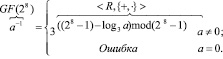. (4)
Наконец, для возведения в степень v заданного элемента a поля GF(28) можно использовать формулу, применив операцию модулярного умножения логарифмов:
- 
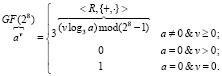(5)
Пример 1. Найдем сумму элементов расширенного поля GF(28), представленных в виде соответствующих чисел «87» и «131» в десятичной системе счисления. Имеем,
.
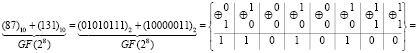
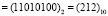Таким образом,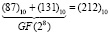 
.
Пример 2. Найдем произведение элементов поля GF(28), представленных в виде соответствующих чисел «87» и «131» в десятичной системе счисления. По таблице логарифмов для поля GF(28) имеем логарифмы элементов: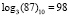 
и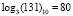 
. Тогда получаем:
.
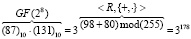По таблице степеней для поля GF(28) имеем 3178 = (193)10. Таким образом:
.
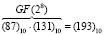Пример 3. Найдем отношение элементов поля GF(28), представленных в виде соответствующих чисел «131» и «193» в десятичной системе счисления. По таблице логарифмов для поля GF(28) имеем логарифмы элементов: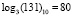 
и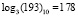 
. Тогда получаем:
.
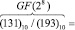
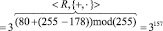По таблице степеней имеем 3157 = (191)10. Таким образом:
.
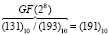Пример 4. Найдем обратный элемент по умножению для элемента «191», представленного в десятичном виде. По таблице логарифмов имеем логарифм элемента: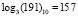 
. Тогда обратный элемент:
.
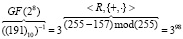По таблице степеней имеем 398 = (87)10. Таким образом:
.
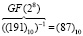Пример 5. Возведем элемент «13», представленный в десятичном виде, в заданную степень v = 17. По таблице логарифмов для поля GF(28) имеем логарифм элемента: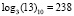 
. Тогда по формуле получаем:
.
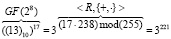По таблице степеней имеем 3221 = (81)10. Таким образом,
.
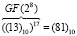Схемы прямого умножение и инвертирование элементов поля Галуа GF(28) в криптографическом стандарте AES. В случае необходимости высокопроизводительного прямого умножения элементов a и b поля Галуа GF(28), можно использовать заранее подготовленную свертку многочленов a(x) и b(x) по модулю p(x) = x8 + x4 + x3 + x + 1:
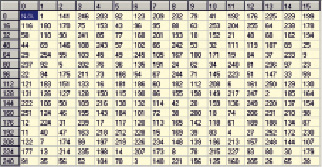
Рис. 3. Таблица обратных элементов по умножению для поля Галуа GF(28) для AES
Аппаратную реализацию схемы умножения мы не будем приводить в силу ее громоздкости. Отметим лишь, что ее несложно построить при помощи 64 двухвходовых логических элементов «И» и 8 многовходовых сумматоров по модулю 2.
Также в случае необходимости применения высокопроизводительного вычислителя обратного элемента по умножению (для ускорения операции деления), можно использовать заранее вычисленную таблицу обратных элементов по умножению.
Ниже на рис. 3 (в виде матрицы 16 x 16) приведены обратные элементы по умножению для элементов поля Галуа GF(28), представленные в десятичном виде. Обратные элементы по умножению расположены построчно (по 16 в строке) для всех элементов поля, начиная с (a)10 = 0, заканчивая (a)10 = 255. Заметим, что обратного элемента по умножению для нуля не существует (соответствующая ячейка «N/A»).
Для аппаратной реализации таблицы можно использовать ПЗУ емкостью 256 x 8 бит.
Заключение
Таким образом, в рамках данной статьи рассмотрено поле Галуа GF(28) на базе неприводимого многочлена p(x) = x8 + x4 + x3 + x + 1, которое применяется в криптографическом стандарте AES (усовершенствованный стандарт шифрования). Также рассмотрены схема формирования таблиц степеней и логарифмов на базе примитивного элемента (α)10 = 3, формулы сложения, умножения и деления, а также инвертирования элементов и возведения в заданную степень. Приведены примеры выполнения арифметических операций с элементами поля. Также рассмотрены высокопроизводительные схемы прямого умножения и инвертирования элементов поля.
Полученные результаты могут быть использованы при разработке эффективных программных и аппаратных реализаций вычислительных блоков в рамках шифрования и дешифрования информации по криптографическому стандарту AES.