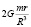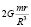Взаимосвязь между солнечной активностью и положением планет является темой исследований в течение многих десятилетий. Предположение о такой взаимосвязи делалось неоднократно в работах разных авторов, начиная с Р. Вольфа, который является основоположником данного направления [1]. По его мнению, солнечная активность вызывается приливным воздействием планет на Солнце. С тех пор много десятилетий подряд в разных источниках высказываются гипотезы о характере влияния планет солнечной системы на циклы активности Солнца. В 1960-1970-х годах в СССР этому вопросу были посвящены публикации В. Шувалова о взаимосвязи солнечного цикла и расположения планет по долготе, например [2]. Проводятся подобные исследования и в наше время, например [3, 4, 5]. Однако точно установить взаимосвязь между солнечными циклами и влиянием планет до сих пор не удалось: не существует какой-либо подтверждённой модели происхождения солнечного цикла и не разработаны методики предсказания особенностей и времени следующих циклов. Ю.В. Витинский пишет: «период обращения Юпитера вокруг Солнца (11,7 года) поразительно близок к средней длине цикла солнечной активности (11,1 года)» [6]. В то же время, есть обоснованные мнения, что приливное воздействие планет на Солнце настолько мало, что солнечные циклы нельзя объяснить его влиянием. «Приливное воздействие планет на Солнце не в состоянии увеличить его радиус больше, чем на 1 мм» [6]. В связи с этим в [6] также приводятся гипотезы, описывающие цикличность активности Солнца вовсе без учёта влияния планет, например, теория солнечного динамо.
В новом веке по-прежнему продолжает оставаться много необъяснимых явлений, связанных с солнечным циклом. Так, неожиданностью для научного сообщества стало запоздание цикла: «Продолжавшийся около трех лет беспрецедентный период необычно низкой активности Солнца закончился. Об этом заявил ведущий британский научный астрофизический центр – Лаборатория Рутерфорд Эпплтон. Мировая наука с облегчением вздохнула, Солнце вышло из загадочного для ученых периода затяжной спячки» [7]. «Текущий 24-й цикл является аномальным по сравнению с предшествующими циклами» [8].
Обратимся к результатам, связанным со смещение барицентра Солнца. «Ничтожно малым получилось и влияние отклонения положения центра Солнца от положения центра масс Солнечной системы». [6]. Тем не менее, есть результаты о взаимосвязи солнечных циклов и движения Солнца относительно центра масс Солнечной системы (ЦМСС). Так, в [9] показано, что экстремумы орбитального ускорения Солнца соответствуют максимумам солнечной активности.
«Причина появления продолжительных минимумов солнечной активности неизвестна» [8] . «Остаётся большим вопросом, каков же механизм этого влияния» [3].
Итак, обилие противоречивых мнений и результатов в исследовании проблемы солнечных циклов, безусловно, свидетельствует о том, что проблема актуальна и далека от полного решения. В связи со всем сказанным, тема исследования комплекса возможных причин солнечного цикла продолжает оставаться актуальной.
В работе [3] рассчитываются средние разности долгот (СРД) для Юпитера, Венеры и Земли. Однако параметр «СРД» обладает следующими недостатками: он не учитывает массы планет и форму их орбит, а ведь именно масса и расстояние от Солнца являются основными параметрами, от которых зависит гравитационное воздействие. На рис. 2 работы [4, с. 58] график зависимости гелиоцентрической долготы каждой планеты от времени есть прямая линия, т.е., по-видимому, в данном приближении угловая скорость предполагается постоянной, как если бы движение происходило по круговой орбите. Однако на самом деле орбиты планет эллиптические, и угловая скорость меняется со временем. Кроме того, параметр СРД никак не учитывает приближение и удаление планеты от Солнца, а ведь эти вариации настолько существенны, что пренебрегать ими нельзя: одни лишь только вариации гравитационных сил со стороны Юпитера превышают абсолютную величину воздействия любой из других планет. Это будет показано в табл. 1 и 2 в п. 3 данной работы.
В [4, с. 60] приводится расчёт сил взаимного притяжения, где для Земли сила полагается равной единице. Очевидно, орбиты планет при этом считаются круговыми (т.к. все указанные параметры являются константами). Это весьма грубое приближение, не позволяющее выявить влияние эллиптичности орбит на исследуемые процессы. Очевидно, кроме учитываемых Шуваловым в [2] и Охлопковым [3, 4, 5] конфигураций расположения планет и их сгруппированности по гелиоцентрической долготе, необходимо учитывать также и массы планет, и их расстояния до Солнца, причём с учётом приближения и удаления вследствие эллиптичности орбиты. Само по себе рассмотрение конфигураций планет без учёта других факторов, несмотря на то, что оно регулярно становится предметом исследований на протяжении десятилетий, не привело к полному решению проблемы ни в 1960-1970-х, ни в настоящее время. Очевидно, одним лишь расположением планет по долготе не исчерпывается вся совокупность причин, порождающих солнечные циклы, иначе точное предсказание солнечной активности в любой будущий момент времени было бы уже решённой задачей. Видимо, причина этого в том, что «рассуждения, которые выдвигались для обоснования гипотезы планетной обусловленности солнечной активности, были исключительно эмпирико-статистическими. Ни о каких строгих физических расчетах не было и речи» [6].
Хотелось бы заострить внимание на следующем противоречии. В [3] при исследовании расстояния между центрами масс Солнца и солнечной системы отмечается периодичность в 19,86 года, вызванная соединением Юпитера и Сатурна. «Наибольший по амплитуде пик – 19,86 года – соответствует соединению Юпитера и Сатурна». [3, с. 139]. Но ведь солнечный цикл составляет не 19,86 а около 11 лет, так что очевидно, соединением планет-гигантов процесс не объясняется. Более того, как будет показано ниже, приближение и удаление Юпитера вследствие эллиптичности его орбиты играет намного большую роль, чем соединение с Сатурном. Соединение с Сатурном добавляет к силе максимум 20•10–9 Н/кг, тогда как приближение Юпитера к перигелию увеличивает его гравитационное воздействие на Солнце на величину 41•10–9 Н/кг.
В [10] приводится расчёт среднего ускорения, порождаемого каждой планетой, в реальных физических величинах (10–9 Н/кг). Позже тема была продолжена в [11], где приведена подробная таблица, учитывающая форму планетных орбит, т.е. показаны силы в момент нахождения в перигелии и афелии. В данной статье делается попытка дать подробную оценку гравитационного влияния Юпитера на Солнце в различные моменты времени с целью оценить возможность его влияния на формирование солнечного цикла.
Возможные причинноследственные связи
Следует сразу отметить, что изучаемые причинно-следственные связи между солнечной активностью и положением планет могут носить лишь односторонний характер. Траектории движения планет обусловлены законами небесной механики и не зависят от наличия или отсутствия пятен на Солнце, а вот гравитационное влияние планет может порождать смещение центра масс Солнца, вызывать неравномерности движения и усиливать солнечную активность.
Сгруппированность планет по долготе приводит к увеличению равнодействующей внешней гравитационной силы, действующей на Солнце, а следовательно, к усилению солнечной активности, однако сам механизм этого явления пока неизвестен. Дело в том, что можно выделить два различных процесса, происходящих из-за сгруппированности планет:
1) смещение барицентра Солнца относительно центра масс солнечной системы.
2) усиление приливного воздействия.
Фактически, в разных работах авторы неявно как раз и подразумевают два различных типа влияния планет на Солнце: «барицентрическое» и «приливное». Однако, точно неизвестно, какое из этих влияний вносит больший вклад и в конечном итоге определяет характер солнечной активности. Следует разделять эти процессы как минимум потому, что вклад одной и той же планеты в первый и второй процесс различны. При расстоянии R планеты от Солнца, гравитационное притяжение, вызывающее добавочное ускорение центра масс Солнца, пропорционально R–2, в то время как приливное воздействие пропорционально величине R–3. Величина вертикальной составляющей приливного ускорения в зависимости от зенитного расстояния небесного тела определяется известной формулой:
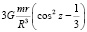
где z – зенитное расстояние тяготеющего небесного тела, m – масса тяготеющего небесного тела, R – расстояние до тяготеющего небесного тела, G – гравитационная постоянная, r – радиус Солнца. Таким образом, максимальное приливное воздействие для тех точек, для которых тяготеющее тело находится в зените, равно 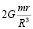 .
.
Итак, для воздействий, пропорциональных R–2 и R–3 соответственно, роль планет распределяется по-разному. Для приливного воздействия роль Венеры и Земли сопоставима с ролью Юпитера, а влияние Сатурна на порядок меньше. В то же время для барицентрического воздействия доля влияния Юпитера в 10 раз превосходит роль Венеры, Земли и Сатурна (см. табл. 1, 2 в пункте 3 данной работы).
В работе [12] была предпринята попытка разделить два разных явления. Вводятся понятия «W-активность» и «B-активность». W-активность отождествляется с числом солнечных пятен, а B-активность – с движением барицентра Солнца. Однако, на мой взгляд, ошибочно утверждается, что планеты-гиганты ответственны за B-активность, а планеты земной группы – именно за W-активность. На самом деле, Юпитер вносит самый значительный вклад также и в приливное влияние планет на Солнце, то есть влияет и на то, что в [12] называется «W-активность». По моему мнению, нет двух разных типов активности Солнца, а есть два различных физических процесса, посредством которых планеты могут оказывать влияние на активность Солнца. Движение барицентра Солнца – это не какая-то отдельная так называемая «B-активность», а процесс, который, наряду с приливным воздействием, приводит к изменению солнечной активности. Имеет место комбинированный комплекс процессов, связанных как со смещением центра масс солнечной системы относительно барицентра Солнца, так и с приливным воздействием планет на Солнце.
Очевидно, что Юпитер является самой массивной планетой, однако со всей определённостью до настоящего времени неизвестно, является ли именно Юпитер причиной 11-летнего солнечного цикла, и если да, то каков механизм этого влияния. Не исключено, что близость периода обращения Юпитера к средней продолжительности солнечного цикла может оказаться совпадением. Взаимосвязи носят более сложный и неоднозначный характер, и движение Юпитера может лишь запускать какие-либо процессы, которые развиваются не одномоментно. Более того, структура солнечных циклов не является строго периодической, а подвержена значительным вариациям по длительности от 8 до 15 лет [13], в то время как, очевидно, период обращения Юпитера не подвержен таким вариациям. Также известно, что аналогичные процессы изменения активности происходят не только на Солнце, но и многих звёздах, сходных по строению с Солнцем. Это показывают авторы работы [13], опираясь на результаты исследований [14, 15].
Также хотелось бы заострить внимание на следующих логических выводах, которые, при кажущейся очевидности, остаются в тени и явно не прописаны в литературе.
А) Структура солнечных циклов не является строго периодической, а подвержена значительным вариациям по длительности, в то время как, очевидно, период обращения каждой планеты не подвержен столь значительным вариациям.
Б) Вращение планет, происходящее по законам Кеплера, не претерпело никаких аномальных изменений за время перехода от 23-го цикла к 24-му, а значит, эти аномалии цикла, упоминаемые в [8], однозначно связаны с какими-то внутренними процессами Солнца, а не с влиянием планет.
Из этих двух фактов следует, что особенности солнечных циклов вряд ли в принципе когда-либо будет возможно предсказать, если основываться только на расположении планет солнечной системы. Однако, и влияние расположения планет необходимо исследовать более подробно, в том числе с учётом формы их орбит, обладающих ненулевым эксцентриситетом, что и будет сделано далее.
Численный анализ влияния планет
Вычислим ускорение, порождаемое гравитацией планет солнечной системы, действующее на единицу массы, расположенную в центре солнечной системы. При этом не будем пренебрегать тем фактом, что орбиты имеют ненулевой эксцентриситет, так как именно эти вариации, как мы увидим далее, могут оказаться существенными.
Построим таблицу, отражающую различные параметры гравитационного воздействия планет солнечной системы на центр солнечной системы. Масса, минимальное и максимальное расстояние взяты из известных астрономических справочников. Ускорения и разница ускорений вычислены и сведены в единую таблицу автором впервые в [11].
Таблица 1
Барицентрическое влияние планет на Солнце в зависимости от нахождения в перигелии и афелии
|
Планета |
масса, в 1024 кг. |
минимальное расстояние от Солнца, млн км. |
максимальное расстояние от Солнца, млн км |
Максимальное ускорение, в 10–9 Н/кг. |
Минимальное ускорение, в 10–9 Н/кг. |
Разница, в 10–9 Н/кг. |
|
Юпитер |
1899,77 |
740,57 |
816,52 |
231,1132 |
190,1181 |
40,9951 |
|
Венера |
4,87 |
107,4 |
109 |
28,1693 |
27,3484 |
0,8209 |
|
Сатурн |
568,92 |
1353,573 |
1513,325 |
20,7178 |
16,5746 |
4,1432 |
|
Земля + Луна |
6,05 |
147,1 |
152,1 |
18,6546 |
17,4483 |
1,2063 |
|
Меркурий |
0,328 |
45,9 |
69,7 |
10,3873 |
4,5047 |
5,8826 |
|
Марс |
0,645 |
206,7 |
249,1 |
1,0072 |
0,6935 |
0,3137 |
|
Уран |
87,25 |
2735 |
3004 |
0,7782 |
0,6451 |
0,1331 |
|
Нептун |
102,787 |
4456 |
4537 |
0,3454 |
0,3331 |
0,0123 |
Примечания к табл. 1.
1. Нахождение планеты в перигелии, очевидно, соответствует максимальному оказываемому ускорению (столбцы 3 и 5 соответственно), а нахождение в афелии, напротив, минимальному ускорению (столбцы 4 и 6).
2. Плутон не учитывается вследствие того, что величина воздействия на несколько порядков меньше, чем 10–9 Н/кг. Вместо Земли учтена система «Земля + Луна». Это сделано потому, что Луна является наиболее массивным спутником (по отношению к своей планете) среди всех планет солнечной системы, при этом расположена в несколько раз ближе к Солнцу, чем подобные (по массе) спутники, имеющиеся у планет-гигантов. Поэтому более корректно будет при изучении влияния планет на Солнце учитывать не саму Землю, а общую массу Земли и Луны.
3. Сортировка произведена по убыванию по максимальному оказываемому ускорению (столбец 5). Ускорение в 5, 6, 7 столбцах вычисляется по формуле 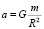 .
.
Из этих данных видно, что воздействие Юпитера на единицу массы в центре солнечной системы на порядок превышает воздействие других планет, и составляет около 2•10–7 Н/кг, тогда как для следующих по силе воздействия планет эта величина около 2•10–8 Н/кг. Но отсюда виден ещё более важный факт: даже вариации силы со стороны Юпитера из-за его приближения и удаления от Солнца вследствие эллиптичности орбиты, составляют около 4•10–8 Н/кг, то есть численно превышают абсолютное значение силы, порождаемой любой другой планетой (около 2•10–8 Н/кг). В большинстве периодов времени, исключая лишь те короткие периоды, когда Венера, Земля и Сатурн расположены почти на одной гелиоцентрической долготе, вариации барицентрического гравитационного воздействия, оказываемого на Солнце со стороны Юпитера, превышают не только воздействие каждой из других планет, но даже их суммарное воздействие. Это может свидетельствовать в пользу наличия причинно-следственной взаимосвязи между циклами солнечной активности и вращением Юпитера. Если солнечный цикл во многом зависит от барицентрического влияния планетной системы, то именно влияние Юпитера является определяющим, причём это воздействие связано именно с эллиптичностью орбиты Юпитера. Вариации барицентрического гравитационного воздействия Юпитера при движении по орбите с эксцентриситетом 0,048 есть величина того же порядка, что и суммарное воздействие всех остальных планет, вместе взятых.
Рассмотрим приливное влияние планет на Солнце при нахождении в перигелии и афелии и вариации вследствие эллиптичности орбит планет. Напомним, что максимальное приливное воздействие для точек, для которых тяготеющее тело видно в зените, равно 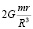 , что можно записать в виде
, что можно записать в виде 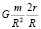 . Тогда очевидно, что для получения численных характеристик приливного воздействия, нужно величины, полученные ранее в трёх последних столбцах табл. 1, домножить на коэффициент вида
. Тогда очевидно, что для получения численных характеристик приливного воздействия, нужно величины, полученные ранее в трёх последних столбцах табл. 1, домножить на коэффициент вида 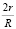 . Учитывая, что радиус Солнца r = 0,696 млн км, дополнительный коэффициент составит величину
. Учитывая, что радиус Солнца r = 0,696 млн км, дополнительный коэффициент составит величину 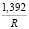 . При этом получаются достаточно малые величины, которые для удобства выражены не в 10–9 Н/кг, а в 10–11 Н/кг.
. При этом получаются достаточно малые величины, которые для удобства выражены не в 10–9 Н/кг, а в 10–11 Н/кг.
Как видно из табл. 2, влияние каждой из планет на процессы, связанные с приливным воздействием, совсем другое, чем вклад этой же планеты в перераспределение масс и движение барицентра Солнца. В периоды максимального приближения Меркурия к Солнцу, его вклад в приливное воздействие почти достигает той величины, которая связана с Юпитером. Величина приливного воздействия Юпитера при максимальном удалении от Солнца становится меньше, чем приливное воздействие Венеры. Естественно, эти явления невозможно было бы выявить, если рассматривать только гелиоцентрические долготы планет, приближённо считая их орбиту круговой.
Итак, эксцентриситеты орбит играют важную роль, и пренебрегать ими при исследовании влияния планет на солнечные циклы нельзя. Учёт только гелиоцентрических долгот планет в различных работах, посвящённых влиянию планет на циклы Солнца, не позволял выявить эти взаимосвязи.
Таблица 2
Приливное влияние планет на Солнце в зависимости от нахождения в перигелии и афелии
|
Планета |
масса, в 1024 кг. |
минимальное расстояние от Солнца, млн км. |
максимальное расстояние от Солнца, млн км |
Максимальное
10–11 Н/кг. |
Минимальное
10–11 Н/кг. |
Разница, в 10–11 Н/кг. |
|
Юпитер |
1899,77 |
740,57 |
816,52 |
43,44 |
32,41 |
11,03 |
|
Венера |
4,87 |
107,4 |
109 |
36,51 |
34,93 |
1,58 |
|
Меркурий |
0,328 |
45,9 |
69,7 |
31,50 |
9,00 |
22,50 |
|
Земля + Луна |
6,05 |
147,1 |
152,1 |
17,65 |
15,97 |
1,68 |
|
Сатурн |
568,92 |
1353,573 |
1513,325 |
2,13 |
1,53 |
0,60 |
|
Марс |
0,645 |
206,7 |
249,1 |
0,68 |
0,39 |
0,29 |
|
Уран |
87,25 |
2735 |
3004 |
0,04 |
0,03 |
0,01 |
|
Нептун |
102,787 |
4456 |
4537 |
0,0108 |
0,0102 |
0,0006 |
Заключение
1. Необходимо явно разделять два разных типа гравитацонного воздействия – барицентрическое и приливное. Оба этих воздействия могут приводить к увеличению солнечной активности, однако вклад каждой планеты в тот или другой тип воздействия различен.
2. При исследовании влияния планет на солнечную активность эксцентриситет орбиты играет важную роль, и пренебрегать им при исследовании солнечных циклов нельзя.