На основе экспериментальных результатов установлено, что при термическом распада радиационно-наведенных дефектов в ионных кристаллах играют ионные процессы, приводящие к превращению наведенных дефектов в другие менее устойчивые образования.
В радиационно-ионных процессах подвижные ионные дефекты имеют конечную длину свободного пробега, поэтому для определения кинетики распада центров следует использовать диффузионную теорию рекомбинации. На основе этой теории рекомбинации получено кинетическое уравнение радиационно-ионных процессов отжига радиационно-наведенных дефектов в ионных кристаллах [1–3].
Закономерности взаимодействия подвижных ионных дефектов и центров окраски определяется концентрацией подвижных дефектов n, их диффузии Д
,
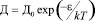энергией активации ε, концентрацией центров окраски N и температурой Т.
Выразив n через N
,
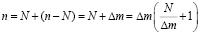где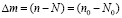 
– разность концентрации подвижных ионных дефектов n и центров окраски N), получим дифференциальное уравнение:
,
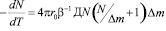характеризующей скорость взаимодействия рекомбинирующих частиц, где β=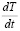 
– скорость нагрева.
Решение этого уравнения будет иметь следующий вид:
.
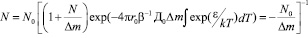Из этого уравнения были получены более простые случаи:
а) если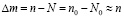 
, (то есть, n>>N, n0>>N0), тогда получим одностадийные кривые термического отжига дефектов по реакции 1-го порядка:
.
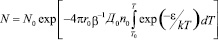б) если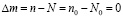 
, (то есть, n=N, n0=N0), тогда получим одностадийные кривые термического отжига дефектов, но по реакции II порядка:
;
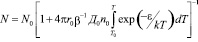в) если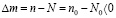 
(то есть, n=N, n0=N0),
В этом случае процесс отжига после первой стадии приостанавливается, не доходя до конца, а общий процесс термического отжига дефектов будет многостадийным.
Обозначив
,
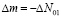где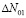 
– концентрации центров данного типа, оставшиеся после первой стадии распада), получим решение кинетического уравнения в следующем виде:
.
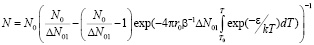Из этого уравнения при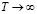 
получаем:
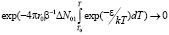
и в конце первой стадии имеем:
.
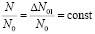То есть процесс термического отжига останавливается не доходя до конца.
Для дальнейшего распада центров окраски данного типа необходимо наличие подвижных дефектов другого типа.
Если концентрации подвижных дефектов второго типа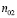 
равна концентрации оставшихся центров данного типа
,
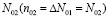то процесс динамического отжига на второй стадии доходит до конца по реакции II порядка.
Тогда для второй стадии термического отжига имеем:
.
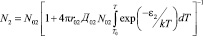В этом случае
,
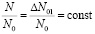то есть процесс начинает действовать для оставшейся после первой стадии концентрации центров. Подставим вместо
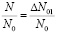
оставшееся после первой стадии термического отжига его значение, тогда получим следующее:
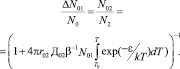
Это выражение определяет вторую стадию термического отжига и начинает действовать только на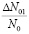 
.
Тогда двухстадийная кривая термического отжига, происходящая по кинетике II-го порядка имеет следующий вид:
.
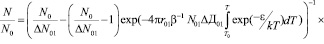
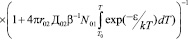Таким образом, исходя из различных соотношений между начальными конценрациями радиационно-наведенных центров и подвижных диффузионных дефектов можно объяснить одностадийных или двух- и более стадийных процессов распада радиационных центров. На основе этой гипотезы получены кинетическое уравнение и его решение для изотермического случая.