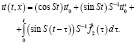Известно, что задача о движении упругой среды в полости W, уравнение кинетического момента всей системы, краевые условия в подвижной системе координат и начальные условия имеют вид:
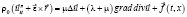 , (1)
, (1)
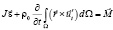 , (2)
, (2)
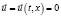 на
на 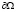 , (3)
, (3)
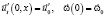 . (4)
. (4)
Задача о нахождении обобщенных решений поставленной задачи сводится к решению задачи Коши для операторного уравнения (см. [1, 2])
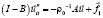 , (5)
, (5)
где A – порождающий оператор гильбертовой пары 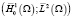 , оператор B имеет вид
, оператор B имеет вид
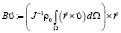 ,
,
а 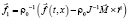 .
.
Доказывается, что при
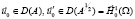
и непрерывно дифференцируемой по t функцией 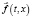 единственное решение задачи (1) – (4) находится по формуле
единственное решение задачи (1) – (4) находится по формуле