Рассмотрим задачу Коши:
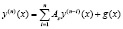; (1)
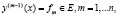(2)
где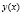 
– функции в локально выпуклом пространстве 
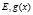– голоморфная в точке 
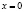функция со значениями в E, A – попарно коммутирующие линейные непрерывные операторы в E.
Введем обозначения:
N0 – неотрицательные целые числа;
,
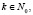
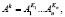
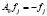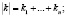
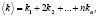
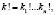
J – интегральный оператор,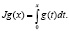 
Будем полагать, что абсолютно в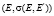 
и равномерно по x в некоторой окрестности нуля
;
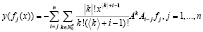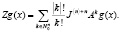
При сделанных предположениях решение задачи (1) – (2) имеет вид
.
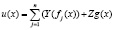