Рассмотрим m-мерную алгебру Ли g. Пусть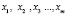 
– базис алгебры g, коммутационные соотношения имеют вид
,
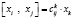где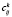 
– структурные константы g.
Определим конечномерные алгебры Ли, допускающие умножение своих базисных элементов на числа вида εp (ε>0, p – целое, положительное число) без изменения своих структурных констант.
Рассмотрим линейное преобразование Te алгебры g, имеющее в базисе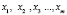 
, матрицу вида
,
где e> 0,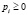 
, 
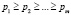. (1)
Алгебру g назовем алгеброй, допускающей преобразование, если существует такое Te вида (1), что
,
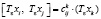где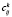 
– структурные константы g.
Можно показать, что если алгебра допускает e – преобразование, то должны выполняться условия
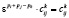
для всех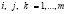 
.
Эти соотношения и определяют условия, связывающие числа pkи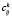 
.
Теорема. Если алгебра Ли допускает e-преобразование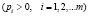 
, то g – разрешимая алгебра Ли.