Ученику начальной школы трудно дается запомнить написание слова медведь, в тетрадке появляются и мидведь, и мэдведь. Но стоит задать вопрос: «А что любит больше всего медведь?», как образовавшая ассоциация медведь - мёд, сразу же помогает запоминанию правильного написания этого словарного слова, знакомого ребенку с детства.
Интеллигент. Как только ни пишут это слово! Простой же вопрос: «ел ли интеллигент?», позволяет не делать больше никаких уточнений и по написанию удвоенной буквы л, и с написанием букв е и и в нем. Ассоциация «окно» - для запоминания слов исключений с удвоенным написанием согласных -нн- в суффиксе прилагательных оловянный, деревянный, стеклянный, - это пожалуй самый известный пример использования учителем ассоциаций в обучении.
Но это примеры ассоциаций, которые образованны учителем специально и направлены на оказание практической помощи учащимся в запоминании правил или слов исключений. Однако существуют ассоциации, спонтанно образующиеся в сознании ученика, коварство которых заключено в том, что к ошибкам они ведут не непосредственно в ходе изучения темы, а намного позже.
Пожалуй, каждому учителю математики старших классов знакомы такие записи, выдаваемые за решение неравенства x2 < 4:
x2 < 4,
x ≤ ±2.
Ответ: x ≤ ±2.
Это и есть пример ошибки, полученной из-за образования неверной ассоциации.
Как же возникает такая ошибка? Ведь ученики, пришедшие в старшие классы, знакомы и с методом интервалов, и с графическим способом решения квадратичных неравенств с помощью параболы, а она все равно появилась.
Чтобы ответить на этот вопрос, необходимо вернуться в восьмой класс, где учащиеся впервые знакомятся с алгоритмом решения неполных квадратных уравнений. Вот цепочка преобразований, которой сопровождается решение уравнения x2 - 4 = 0:
x2 - 4 = 0,
x2 = 4,
x = ±2
Ответ: ±2.
Такие решения ученик может увидеть не только на классной доске, но и в некоторых пособиях, и в жутком порождении современности - в решебниках.
Придя в девятый класс и встретив неравенство, даже уже познакомившись с методом интервалов, он движется все равно в том направлении, в котором «рука писать привыкла». Все это происходит из-за недостаточного внимания к построению выполняемых записей на доске, по невозможности спрогнозировать учителю появление впоследствии ошибок из-за таких решений.
Как же предупредить появление таких ошибок? Ведь исправлять гораздо сложнее, чем учить!
Методика предупреждения таких ошибок школьников в процессе изучения математики, основана на том, что такие ошибки отсрочены по времени изучения данной темы и включает в себя:
- составление учителем «карты ошибок возникающих ассоциативно», по содержанию всего школьного курса математики;
- выделение фрагментов-образцов, ведущих впоследствии к образованию неверной ассоциативной связи, и их исключение;
- построение цепочек заданий, препятствующих образованию неверной ассоциативной связи;
- формирование опережающей ассоциации, в том случае, когда неверная ассоциативная связь уже образована
Раскроем некоторые из элементов этой методики. Фрагмент «карты ошибок, возникающих ассоциативно»:
|
№ |
Ошибка |
Ассоциативная связь |
|
|
х2 < 4 , |
Образец решения неполных квадратных уравнений: |
|
1. |
х ≤±2. |
x2 = 4. |
|
|
Ответ: х < ±2. |
x = ±2 |
|
2. |
x/4 ≤9/x х2 ≤ 36. |
Правило «крест-накрест» для пропорций (эта же связь дополнительно получает подкрепление на уроках химии). |
|
3 |
(-3)+(-5)=8. |
Хорошо запоминающаяся фраза «минус на минус дает плюс». |
|
4 |
√х +11 = 1 - х x2 - 3x - 10 = 0, х=5 или х= -2. В ответ ученик записывает число 5. |
«Там, где корень, там не место отрицательным числам». Путаница между числом и значением выражения. |
|
5 |
sin4x=4sinxcosx |
Закрепление sin2x=2sinxcosx, без обобщения. |
|
6 |
22 х-1 - 2х = 8, 22 х-1 - 2х = 23, 2 х -1 - х = 3, х = 4. |
«Приравниваем показатели». Не произведено обобщение на уровне свойств функций, которые позволяют решать целый класс уравнений вида f(а) = f/(β), в случае если функция / монотонна. |
|
7 |
log2 0,7; sin 4 - положительные числа |
«У отрицательного числа должен быть знак минус». Нет понимания того, что "минус" - это не только отрицательный, это - обозначение противоположного элемента. |
Из карты можно увидеть что, например, успешность в решении иррациональных уравнений закладывается задолго до изучения самого алгоритма решения. Помимо чисто операционных навыков: умение равносильно переносить слагаемые из одной части уравнения в другую, правильно возводить двучлены во вторую степень, решать квадратные уравнения, необходимо чтобы учащиеся не путали понятия отрицательного числа и отрицательного значения выражения. В противном случае, как только появится отрицательное число, проверка полученных корней в уравнении-следствии станет формальной, поскольку сработает ассоциация с тем, что «там, где знак радикала, там не место отрицательным числам».
В итоге, для данной темы, получается комплексная методическая работа, которая определяет содержание урока:
во-первых, у учащихся, еще в курсе алгебры 7 и 8 классов, необходимо сформировать четкое представление о значении выражения и об области определения арифметического квадратного корня;
во-вторых, непосредственно при изучении темы решение иррациональных уравнений необходимо построить такую цепочку упражнений, в которой была бы разрушена связь отрицательный корень - посторонний корень.
Для уроков в 8 классе подойдут такие задания:
а) дано выражение √5 - х , выберите те из чисел 3; -2; 7; -5; 9, при которых оно существует;
б) какие из чисел 5; -2; 3; -5, принадлежат области значений выражения 3-√х. в ходе их выполнения учащимся предстоит глубже разобраться в свойствах арифметического квадратного корня, что поможет им в освоении алгоритма решения иррациональных уравнений.
Последовательность упражнений для первого урока решения иррациональных уравнений, составляется такой, чтобы в ней не встретилось в первых задачах сочетание корней разных знаков у уравнения-следствия:
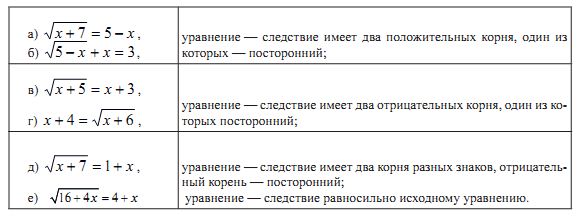
Покажем, на актуальном примере - методе декомпозиции решения неравенств, как работает представленная методика урока предупреждения ошибок в части выделения фрагментов-образцов, ведущих впоследствии к образованию неверной ассоциативной связи, и их исключении.
Неравенство
![]()
с точки зрения предупреждения ошибок представляет собой очень поучительный пример.
Действительно, преобразование исходного неравенства к неравенству
![]()
является несложным и основано на простых и хорошо известных свойствах логарифма и определения а-1 = 1/a. Следующий же шаг может а быть ошибочным, так переход к неравенству
![]()
при x > 1, является неравносильным, поскольку
![]()
Но и преобразование к неравенству
![]()
в силу возникающей неверной ассоциации 3Har(l0gab-l0gac-l0gad)=3HaK[a-1)(b-c-d), идущей от формального запоминания «секретных приемов», не имеющих должного обоснования, как это делалось ранее в математических и физико-математических классах, может послужить впоследствии шагом к неверному переходу
![]()
Правильное и акцентированное решение позволит сосредоточить внимание учащихся на верном применении свойства знак(logab-logac)≡знак(a-1)(b-c), что определяет выполнение пункта 20 предложенной методики предупреждения ошибок, вызванных ассоциативной связью.
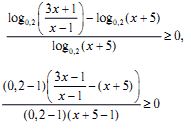
Необходимо обратить так же внимание на то, что при применении метода декомпозиции неравенств следует полностью учитывать все неравенства-ограничения на область определения соответствующих выражений. В то же время, при применении метода решения неравенств, основанного на использовании свойств монотонности соответствующих функций, этого можно избежать и потому, в таком случае, решение может быть существенно более простым.
Умение строить урок предупреждая появление ошибок, особенно из-за возникающей неверной ассоциативной связи, ведение учителем соответствующей поисковой деятельности предопределяет повышение методической грамотности педагога, позволяет ему существенным образом оптимизировать учебный процесс, снизить затраты учебного времени на вынужденную необходимость исправления ошибок идущих не от «старых недоработок», а из-за неверных ассоциаций. В конечном итоге, предупреждать ошибки, а не корректировать их, это поистине высокое учительское мастерство, которое закладывается не только кропотливым трудом, но и желанием работать на развитие, определяет индивидуальный почерк учителя.

