Любые экономические данные представляют собой количественные характеристики изучаемых экономических объектов. Числовые значения экономического показателя формируются под воздействием некоторого множества факторов, при этом не все факторы доступны внешнему контролю и могут принимать случайные значения. Этот факт вызывает необходимость применения эконометрических методов для последующего эконометрического анализа и принятия научно-обоснованных экономических решений. В приложении к аналитической оценке результатов деятельности на микро- макроуровне он выступает тем инструментом, который позволяет найти количественное выражение взаимосвязей между исследуемым показателем и факторами, влияющими на его величину.
Цель исследования – на основе официальной статистической информации выполнить эконометрический анализ экономических показателей крупной отрасли Республики Казахстан – горнодобывающей промышленности. В ходе исследования применялись эконометрические методы обработки и анализа исходной информации.
Эконометрический анализ состоит из следующих этапов:
- предварительный статистический анализ исходных данных;
- установление факта наличия связи, определение её направления и формы;
- установление степени тесноты связи между признаками;
- построение регрессионной модели и оценка её адекватности.
I. Статистический анализ данных объединяет совокупность статистических методов, которые основаны на формализованном представлении исходной информации в многомерном пространстве и позволяют выявлять неявные, но объективно существующие закономерности в структуре и тенденциях развития изучаемых социально-экономических явлений и процессов.
а) Одно из условий статистического анализа данных – однородность исследуемой информации относительно распределения её около среднего уровня.
Критерием однородности информации служат среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю [1, С. 42].
Среднеквадратическое отклонение показывает абсолютное отклонение наблюдаемых значений от среднеарифметической.
Коэффициент вариации показывает относительную меру отклонения отдельных значений от среднеарифметической. Чем больше коэффициент вариации, тем относительно больший разброс и меньшая выравненность изучаемых объектов. Изменчивость вариационного ряда принято считать незначительной, если вариация не превышает 10 %, средней – если вариация составляет 10–12 %, значительной – когда она больше 20 %, но не превышает 33 %. Если же вариация выше 33 %, то это свидетельствует о неоднородности информации и необходимости исключения нетипичных наблюдений.
б) Следующее требование к исходной информации – подчинение её закону нормального распределения. Для количественной оценки степени отклонения исходных данных от нормального распределения служат: отношение показателя асимметрии (А) к её ошибке (A/ma) и отношение показателя эксцесса (Е) к его ошибке (E/me).
В симметричном распределении А = 0. Отклонение от нуля указывает на наличие асимметрии в распределении данных около средней величины. Отрицательная асимметрия свидетельствует о том, что преобладают данные с большими значениями, а с меньшими значениями встречаются значительно реже. Положительная асимметрия показывает, что чаще встречаются данные с небольшими значениями.
В нормальном распределении показатель эксцесса Е = 0. Если Е > 0, то данные густо сгруппированы около средней, образуя островершинность. Если Е < 0, то кривая распределения будет плосковершинной. Однако когда отношения A/me, E/me меньше 3, то асимметрия и эксцесс не имеют существенного значения, и исследуемая информация соответствует закону нормального распределения. Следовательно, её можно использовать для корреляционного и регрессионного анализа.
Корреляционный анализ ставит задачу измерить тесноту связи между варьирующими переменными и оценить факторы, оказывающие наибольшее влияние на результативный признак. Для количественной оценки тесноты линейной связи между признаками используется коэффициент корреляции R. Этот коэффициент имеет большое значение при исследовании экономических явлений и процессов, распределение которых близко к нормальному закону [1, С. 55]. Коэффициент детерминации R2 показывает долю вариации результативного признака Y под воздействием изучаемого факторного признака (признаков). Регрессионный анализ предназначен для выбора формы связи, для определения расчётных значений зависимой переменной (результативного признака).
Свойство линейной зависимости некоторого фактора от других факторов называется мультиколлинеарностью. На практике наиболее простым критерием наличия мультиколлинеарности между двумя признаками является значение коэффициента парной корреляции 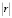 ≥ 0,8. Для устранения мультиколлинеарности необходимо исключить линейные факторы или преобразовать исходные факторные признаки в новые за счёт их укрупнения.
≥ 0,8. Для устранения мультиколлинеарности необходимо исключить линейные факторы или преобразовать исходные факторные признаки в новые за счёт их укрупнения.
в) Оценка адекватности (качества) регрессионной модели.
1. Проверка значимости каждого коэффициента регрессии осуществляется с помощью t – критерия Стьюдента, при этом статистическая существенность связи утверждается при исключении нулевой гипотезы об отсутствии связи.
2. Проверка адекватности всей модели осуществляется на основе F-критерия Фишера. Если расчётное значение Fрасч. > Fтаб. определяемого по таблице F-распределения при уровне значимости a = 0,05 или a = 0,01, то регрессионная модель считается адекватной реальному экономическому явлению.
3) модель должна иметь минимальную ошибку аппроксимации [2, С. 160].
II. Используя официальные статистические данные по отрасли «Горнодобывающая отрасль и разработка карьеров» за 2005–2014 годы (табл. 1), исследуем зависимость объёма промышленной продукции (Y) от факторов, которые могут оказывать на неё влияние: индекса физического объёма промышленной продукции (Х1), числа промышленных предприятий и производств (Х2), численности персонала (Х3), инвестиций в основной капитал (Х4), рентабельности (Х5), индекса цен-предприятий-производителей (Х6). Все расчеты выполнены в MS Excel.
Таблица 1
Основные показатели горнодобывающей отрасли Республики Казахстан
|
Годы |
Объем пром. произв., млрд.тг. |
Индекс физ. объема пром. продукции, в % к пред.году |
Число промышленных предприятий и производств |
Численность персонала, тыс.тг. |
Инвестиции в основной капитал, млрд.тг. |
Рентабель-ность, % |
Индекс цен предприятий производителей, в % к предыдущему году |
|
Y |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
|
|
2005 |
3121,1 |
102,7 |
548 |
154,7 |
540,2 |
88,5 |
138,3 |
|
2006 |
3761,3 |
107 |
578 |
159,3 |
643,9 |
109,8 |
118,7 |
|
2007 |
4445,4 |
102,6 |
655 |
161,2 |
826,5 |
112,5 |
110,8 |
|
2008 |
5229,8 |
105,5 |
695 |
170,3 |
847,8 |
101,5 |
146,4 |
|
2009 |
5502,0 |
107,2 |
744 |
161,4 |
769,9 |
54,1 |
69,8 |
|
2010 |
7419,6 |
107,2 |
672 |
168,1 |
1652,0 |
71,5 |
132,8 |
|
2011 |
10081,3 |
101 |
721 |
182 |
1593,6 |
75,4 |
133,5 |
|
2012 |
10242,1 |
100,4 |
793 |
209,7 |
1599,7 |
71,6 |
104,2 |
|
2013 |
10696,9 |
103,3 |
802 |
207,3 |
1769,4 |
62,1 |
98,5 |
|
2014 |
11060,2 |
98,7 |
966 |
203,3 |
1985,0 |
35,4 |
110,5 |
Примечание. Составлено авторами на основе [3, 4].
Результаты основных статистических характеристик для всей совокупности данных представлены в табл. 2.
Таблица 2
Описательная статистика исходных данных
|
Характеристики статистической совокупности |
Y |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
|
Среднее |
7155,97 |
103,6 |
717,4 |
177,7 |
1222,8 |
78,2 |
116,4 |
|
Стандартная ошибка |
969,4 |
1,0 |
38,0 |
6,8 |
171,5 |
7,9 |
7,2 |
|
Медиана |
6824,7 |
103,0 |
708,0 |
169,2 |
1220,7 |
73,5 |
114,8 |
|
Среднеквадратическое отклонение |
2958,5 |
2,9 |
114,0 |
20,3 |
514,5 |
23,6 |
21,6 |
|
Дисперсия выборки |
9397445,5 |
9,3 |
14442,3 |
458,5 |
294153,7 |
621,4 |
517,0 |
|
Асимметричность |
0,0 |
– 0,1 |
0,7 |
0,7 |
0,1 |
– 0,1 |
– 0,7 |
|
A/ma |
0,02 |
– 0,13 |
0,88 |
0,85 |
0,08 |
– 0,14 |
– 0,94 |
|
Эксцесс |
– 1,8 |
– 1,3 |
1,0 |
– 1,4 |
– 2,0 |
– 0,7 |
0,6 |
|
E/me |
– 1,19 |
– 0,85 |
0,66 |
– 0,93 |
– 1,31 |
– 0,45 |
0,38 |
|
Интервал |
7939,1 |
8,5 |
418,0 |
55,0 |
1444,8 |
77,1 |
76,6 |
|
Минимум |
3121,1 |
98,7 |
548,0 |
154,7 |
540,2 |
35,4 |
69,8 |
|
Максимум |
11060,2 |
107,2 |
966,0 |
209,7 |
1985,0 |
112,5 |
146,4 |
|
Сумма |
72559,7 |
1035,6 |
7174,0 |
1777,3 |
12228,0 |
782,4 |
1163,5 |
|
Счет |
10,0 |
10,0 |
10,0 |
10,0 |
10,0 |
10,0 |
10,0 |
|
Уровень надежности (95 %) |
2192,9 |
2,2 |
86,0 |
15,3 |
388,0 |
17,8 |
16,3 |
|
Коэффициент вариации, % |
31,0 |
2,8 |
15,9 |
11,4 |
42,1 |
30,2 |
18,5 |
В соответствии с полученными коэффициентами вариации (табл. 2) по фактору X1 наблюдается незначительная вариация; среднюю вариацию имеет также один фактор X3; все остальные факторы (за исключением Х4) обладают значительной вариацией, но ее величина не превышает 33 %. Коэффициент вариации фактора Х4 составляет 42,1 %, что свидетельствует о неоднородности представленных данных.
Найденные значения коэффициентов асимметрии, достаточно близкие к нулю за исключением факторов Х2, Х3 указывают, что распределение данных около средних величин симметрично. При этом отрицательная асимметрия по факторам Х1 Х5, Х6 свидетельствует о том, что преобладают данные с большими значениями, а с меньшими значениями встречаются реже. Положительная асимметрия (факторы Х2, Х3, Х4) показывает, что чаще встречаются данные с небольшими значениями.
По факторам Х2, X6 эксцесс больше нуля, это указывает на то, что данные густо сгруппированы около средней, образуя островершинность. По оставшимся 4 факторам величина эксцесса имеет отрицательное значение, что свидетельствует о плосковершинной кривой распределения.
Однако рассчитанные отношения A/ma, E/me меньше 3. Это означает соответствие исследуемой статистической совокупности закону нормального распределения. Следовательно, её можно использовать для корреляционного анализа.
Далее необходимо осуществить выбор факторных признаков для построения регрессионной модели, рассчитать её параметры и оценить адекватность. Результаты корреляционного анализа приведены в табл. 3.
Таблица 3
Матрица парных коэффициентов корреляции
|
Факторы |
Y |
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
Х6 |
|
Y |
1,000 |
||||||
|
Х1 |
– 0,601 |
1,000 |
|||||
|
Х2 |
0,838 |
– 0,564 |
1,000 |
||||
|
Х3 |
0,923 |
– 0,646 |
0,819 |
1,000 |
|||
|
Х4 |
0,955 |
– 0,525 |
0,790 |
0,845 |
1,000 |
||
|
Х5 |
– 0,716 |
0,351 |
– 0,803 |
– 0,603 |
– 0,695 |
1,000 |
|
|
Х6 |
– 0,206 |
– 0,047 |
– 0,414 |
– 0,244 |
– 0,087 |
0,469 |
1,000 |
Анализ строк матрицы (табл. 3) позволил выявить факторы, у которых степень тесноты связи с результативным показателем значительная, поэтому они могут быть включены в модель. Так, наиболее значительная связь с объёмом промышленной продукции наблюдается по фактору Х2 (число промышленных предприятий), Х3 (численность персонала) и Х4 (инвестиции в основной капитал), остальные факторы имеют менее тесную связь с результативным признаком. Однако факторы Х2 и Х3, Х3 и Х4 тесно связаны между собой (rx2x3 = 0,819; rx3x4 = 0,845), что свидетельствует о наличии мультиколлинеарности.
Таким образом, для устранения мультиколлинеарности необходимо исключить факторы Х2 и Х3. Учитывая небольшой объём статистической выборки были исключены факторы Х1 и Х6 как малоинформативные и статистически незначимые.
Результаты регрессионного анализа с использованием двух факторов Х4 и Х5, и обозначениями, принятыми в учебной литературе, представлены в табл. 4–6.
Таблица 4
Показатели регрессионной статистики
|
Множественный коэффициент корреляции, R |
0,958 |
|
Коэффициент детерминации, R2 |
0,917 |
|
Скорректированный R2 |
0,894 |
|
Стандартная ошибка |
1016,193 |
|
Количество наблюдений, n |
10 |
Таблица 5
Показатели дисперсионного анализа
|
Наименование |
df |
SS |
MS |
F |
Значимость F |
|
Регрессия |
2 |
80300813,668 |
40150406,834 |
38,881 |
0,000 |
|
Остаток |
7 |
7228535,933 |
1032647,990 |
||
|
Итого |
9 |
87529349,601 |
Таблица 6
Показатели регрессионного анализа
|
Наименование |
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-значение |
Нижние 95 % |
Верхние 95 % |
|
Y-пересечение |
1938,267 |
2366,662 |
0,819 |
0,440 |
– 3657,998 |
7534,533 |
|
X4 |
5,084 |
0,869 |
5,853 |
0,001 |
3,030 |
7,138 |
|
Х5 |
– 12,762 |
18,899 |
– 0,675 |
0,521 |
– 57,453 |
31,928 |
Множественный коэффициент корреляции R определяет тесноту связи между результативным признаком и факторными признаками. Он даёт такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может служить для сравнения различных моделей с различным числом факторов.
Как следует из данных, представленных в табл. 4 множественный коэффициент корреляции равен 0,958, что свидетельствует о достаточно сильной связи между объёмом производства промышленной продукции и факторными признаками Х4 – инвестициями в основной капитал и Х5 – рентабельностью.
R2 = 0,917, следовательно результативный показатель в среднем на 92 % зависит от факторов Х4 и Х5, а остальные 8 % приходятся на долю случайных, неучтённых факторов. Скорректированный коэффициент детерминации R2 определяет тесноту связи с учётом степеней свободы.
Задача дисперсионного анализа состоит в проверке нулевой гипотезы Н0 о статистической незначимости уравнения регрессии в целом и показателя тесноты связи.
Дисперсионный анализ (табл. 5) показывает, что уравнение регрессии является статистически значимым, при этом вероятность гипотезы об отсутствии связи равна 0.
На основании регрессионного анализа (табл. 6) составлено следующее уравнение регрессии:
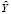 = 1938,267+5,084Х4 – 12,762Х5. (1)
= 1938,267+5,084Х4 – 12,762Х5. (1)
Однако, несмотря на значимость уравнения (1) в целом, не все его факторы являются значимыми. Так, Р – значение фактора Х5 превышает заданный уровень значимости α = 0,05, что характеризует рентабельность как незначимый фактор в данном уравнении регрессии. Значимым фактором, оказывающим наибольшее влияние на объём промышленной продукции, а также имеющим уровень значимости α < 0,05, является фактор Х4 – инвестиции в основной капитал.
Таким образом, из уравнения регрессии нужно исключить фактор Х5, построить однофакторную регрессионную модель и оценить её адекватность.
Полученные результаты:
R = 0,955;
R2 = 0,912;
Fрасч. = 82,946;
tрасч.х5 = 9,107.
Постоянная: a = 441,247;
Коэффициент регрессии: b = 5,491.
Уравнение регрессии примет следующий вид:
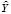 = 441,247 + 5,491х. (2)
= 441,247 + 5,491х. (2)
Значение коэффициента корреляции R = 0,955 близко к единице, что означает сильную корреляционную связь между объёмом промышленного производства и инвестициями в основной капитал. При этом изменение величины Y на 91,2 % обусловлено фактором х – инвестициями в основной капитал.
По таблице t-распределения при уровне значимости a = 0,05 и числе степеней свободы ν = n – k – 1 = 8, tтабл. = 2,306, где k – число факторов. Так как tрасч5 = 9,107 > > tтабл. = 2,306, коэффициент регрессии является статистически значимым.
По таблице F-распределения при уровне значимости a = 0,05, n1 = 1 и n2 = 8 находим Fтабл = 5,318. Так как Fрасч. > Fтабл., уравнение регрессии (2) можно считать адекватным.
Средняя относительная ошибка аппроксимации равна 9,915 %, следовательно, полученная регрессионная модель (2) с достаточно высокой точностью аппроксимирует статистические данные.
Коэффициент регрессии b можно использовать для определения коэффициента эластичности Э, который приближённо показывает, на сколько процентов изменится результативный признак Y при изменении фактора на 1 %:
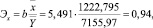 (3)
(3)
т.е. при росте инвестиций в основной капитал на 1 %, объём промышленного производства горнодобывающей отрасли увеличится на 0,94 %.
Выводы
Применение эконометрических методов позволило провести анализ горнодобывающей отрасли Казахстана, установить степень влияния каждого фактора на исследуемый показатель – объём промышленной продукции, более достоверно и объективно оценить результаты деятельности горнодобывающий предприятий.

