![]()
в проблеме оценки прочности материала имеется шестимерная задача, которую сопоставляют с известной одномерной экспериментальной задачей. Эта методологически сложная задача с приемлемой точностью решается в частных случая на ограниченной области определения функции, но другого пути нет из-за отсутствия иных надежных экспериментальных данных. Для пластичных материалов наиболее приемлемой является энергетическая теория прочности, однако, она не может быть применена в существующем виде для нелинейно-упругих материалов. Решение вопроса об условиях прочности зависит исключительно от уровня эксперимента для пространственного и плоского напряженных состояний. В общем случае для одной точки следует рассматривать шесть условий прочности (рассматриваем же мы шесть уравнений состояния в обобщенном законе Гука). Каждую компоненту тензора напряжений необходимо сравнивать с соответствующей для неё функцией допускаемых напряжений:
![]()
Каждая программа испытаний образцов дает одну точку для каждой из шести функций
Совокупность точек , полученных во всех экспериментах, даст в численном виде все функции допускаемых напряжений. Для тензора напряжений общего вида с шестью компонентами эта экспериментальная задача трудно выполнима.
Не нарушая общности, рассматривают эксперимент по главным направлениям, работая с тремя главными напряжениями (вектор-столбец):
![]()
Три условия прочности имеют вид:
![]()
Пусть в момент наступления опасного состояния главные напряжения равны соответственно σ1Ω, σ2Ω , σ3Ω. Для любого из главных напряжений назначаем коэффициент запаса. Пусть нам задано значение коэффициента запаса n1 для σ1. .Тогда получим значение [σ1] (t=tadm) функции главных допускаемых напряжений для данной программы испытаний , соответствующее моменту времени t=tadm:
![]()
где tadm - момент времени испытаний, для которого рассматриваемое напряжение будет принято за допускаемое.
В зависимости от программы испытаний назначаем значения двух других допускаемых напряжений. Заметим, что по функциям [σi] можно найти функции [σij].
Рассмотрим важный распространенный частный случай плоского напряженного состояния, когда действуют нормальные напряжения сх и касательные напряжения ту . В соответствии с (1) условия прочности имеют вид:
![]()
Если нет экспериментальных данных, то можно предположить. что функции [σх], [ту] связаны между собой уравнением эллипса, большей полуосью a которого является традиционное допускаемое нормальное напряжение [σ], а меньшей полуосью b- традиционное касательное допускаемое напряжение [т].
Переходя к полным напряжениям p с учетом (6), имеем условие прочности :
![]()
С учетом того, что т y/σx= [ту ] /[σх], получим из [7] после преобразований:
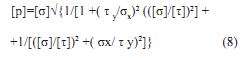
Условия прочности (6) и (7) равносильны. Для конкретного значения [σ] / [т]=2 условие прочности (7) преобразуется в условие прочности по третьей теории, а при [σ] / [т] =√3 оно преобразуется в условие прочности по четвертой теории прочности. Рассмотрим последний случай. В условии (7) имеем:
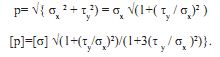
Сопоставляя p и [p], сокращаем на √(1+( ту / σх)2 ) и получаем условие прочности по четвертой теории прочности:
![]()
При других соотношениях между [σ] и [т] результаты не совпадают.
Для трёхмерного случая возможна аппроксимация функции допускаемых напряжений каноническим уравнением эллипсоида и сферы, но это не снимает остроты вопроса о необходимости эмпирических поверхностей.
Предлагаемая теория методологически корректна и при наличии более полных экспериментальных данных может быть с успехом использована в конкретных задачах расчета на прочность конструкций из нелинейно-упругих материалов.
Библиографическая ссылка
Ершов В.И. УСЛОВИЯ ПРОЧНОСТИ ДЛЯ НЕЛИНЕЙНО-УПРУГИХ МАТЕРИАЛОВ // Международный журнал прикладных и фундаментальных исследований. 2010. № 12. С. 109-110;URL: https://applied-research.ru/ru/article/view?id=1014 (дата обращения: 15.02.2026).

