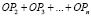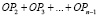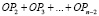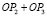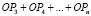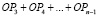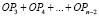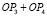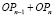Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Шукаев Д.Н. 1 Ламашева Ж.Б. 1

---

1 Казахский национальный исследовательский технический университет имени К.И. Сатпаева

В данной статье разрабатывается конкретная процедура выбора инвестиционных проектов, основанной на функциональных задачах реализации инвестиционной программы банка развития Казахстана, и проводится анализ основных экономических показателей проектов и показателей, характеризующих интересы государства по развитию общественно-значимых отраслей и производств. Рассмотрены три этапа экономической оценки проектов с целью определения оптимальных объемов инвестиций для конечного множества подлежащих инвестированию проектов. На первом этапе проводится анализ основных показателей проектов, на втором идет выбор конечного множества проектов, на третьем происходит оптимальное распределение инвестиций. Сформирован пошаговый алгоритм проведения анализа и выбора объектов инвестирования. Представлены модели и алгоритмы рассмотренных этапов, осуществляемых банком развития, которые являются достаточно универсальными и актуальны для реализации государственной стратегии в данном направлении и осуществления коммерческих интересов любого банка в области инвестирования.

Статья в формате PDF

1652 KB

банки развития

инвестиционный проект

рентабельность

анализ эффективности

экспертные оценки

моделирование случайных параметров

оптимальное распределение ресурсов

1. Акоф Р., Сасиени М. Основы исследования операций. – М.: Мир, 1971. – 536 с.

2. Быстров О.Ф., Поздняков В.Я., Прудников В.М. и др. Управление инвестиционной деятельностью в регионах Российской Федерации. – М.: ИНФРА-М, 2008.

3. Индустриальное развитие с Банком развития Казахстана / Годовой отчет Банка Развития Казахстана за 2014 год. [Алматы], 2015. URL: http://www.kdb.kz/ru/about/reports/ (дата обращения 22.08.2016).

4. Лукасевич И.Я. Анализ финансовых операций. – М.: ЮНИТИ, 2004.

5. Ткаченко А.Н. Оценка эффективности инвестиционных проектов. – Новокузнецк: НФИ КемГУ, 2003. – 78 с.

6. Шукаев Д.Н., Ким Е.Р., Абдикадырова А.А. Функциональные задачи предынвестиционной деятельности банка развития // Международный журнал прикладных и фундаментальных исследований. – 2015. – № 10 (часть 4). – С. 605–610.

7. Biegel J.E. Production control: A quantitative approach. 2nd edition. – New Jersey, USA: Prentice Hall, 1971. – 282 p.

8. Leippold M., Trojani F., Vanini P. Multiperiod mean-variance efficient portfolios with endogenous liabilities // Quantitative Finance. – 2011. – Vol. 11, Iss. 10. – P. 1535–1546.

9. Magni C.A. Investment decisions in the theory of finance: Some antinomies and inconsistencies // European Journal of Operational Research. – 2002. – Vol. 137, Iss. 1. – P. 206–217.

10. Shukayev D.N., Kim E.R., Shukayev M.D., Ergalieva N.O., Mereke A.A. Modeling resource flows and allocations in systems with parallel structure. // Proceedings of the IASTED International Conference Applied Simulation and modeling (ASM 2012). – Napoli, Italy, 2012. – P. 57–63.

Одной из важных задач инвестиционной деятельности банков Казахстана, включая банк развития, является выбор в рамках выделенных для инвестирования средств, наиболее перспективных инвестиционных проектов. Распределение средств в данных условиях требует системного подхода к процессу отбора проектов и оценки их ожидаемой отдачи и риска.

Вопросам финансово-экономической оценки инвестиционных процессов посвящены исследования многих авторов. В работах [4, 8, 9] рассматриваются различные аспекты выбора инвестиционного проектов с учетом различных показателей. Анализ этих исследований показал, что основное внимание уделяется общим подходам к организации инвестиционной деятельности, что не полностью раскрывает проблему формирования и управления инвестиционной политикой с позиции оказания государственной поддержки развитию новых конкурентоспособных отраслей с высоким содержанием добавленной стоимости.

Поэтому в данной статье, основанной на функциональных задачах реализации инвестиционной программы банка развития Казахстана [3, 6], разрабатывается конкретная процедура выбора инвестиционных проектов на основе анализа не только основных экономических показателей проектов, таких как чистый приведенный доход (Net Present Value), внутренняя норма доходности (Internal Rate of Return), индекс рентабельности (Profitability Index) и другие, но и показателей, характеризующих интересы государства по развитию общественно-значимых отраслей и производств.

Анализ эффективности инвестиций

Существуют несколько методов оценки привлекательности инвестиционного проекта, в которых применяются различные показатели для выбора того или иного проекта. В основе каждого метода лежит важный принцип, в соответствии с которым в результате реализации проекта инвестор должен получить прибыль. При этом различные финансовые показатели характеризуют проект с разных сторон в соответствии с интересами различных заинтересованных лиц, связанных с инвестором.

К основным критериям, используемым в анализе инвестиционной деятельности (интегральным показателям), относятся [5]:

– чистый приведенный доход (Net Present Value, NPV)

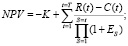
где K – первоначальные инвестиции; R(t) – приток денег в t году; С(t) – отток денег в t году; T – продолжительность жизненного цикла; ЕS – норма дисконта.

– внутренняя норма доходности (Internal Rate of Return, IRR), которая вычисляется как корень уравнения

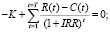
– индекс рентабельности (Profitability Index, PI)

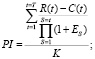
– срок окупаемости инвестиций (Payback Period, РР) – минимальный отрезок времени, по истечении которого NPV становится и остается неотрицательным

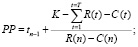
– рентабельность инвестиций – расчет бухгалтерской рентабельности инвестиций (ROI) ведется на основе дохода до процентных и налоговых платежей (EBIT) или дохода после налоговых, но до процентных платежей [EBIT(1 – H)]; что касается величины инвестиций, по отношению к которой определяется рентабельность, то ее находят как среднее между учетной стоимостью активов на начало 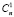и конец 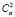рассматриваемого периода

;

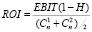– общественная эффективность проекта (OP) характеризует социально-экономические последствия осуществления проекта для общества в целом, т.е. она учитывает не только непосредственные результаты и затраты проекта, но и «внешние» по отношению к проекту затраты и результаты в смежных секторах экономики, экономические, социальные и иные внеэкономические эффекты, как правило, дается качественная оценка (0 < OP < 1).

Все расчеты показателей эффективности (интегральных показателей) выполняются с дисконтированными потоками наличности, представляющими притоки наличности, или поступления денежных средств, и оттоки наличности, или выплаты денежных средств, в процессе реализации проекта.

Показатель NPV отражает непосредственное увеличение капитала компании, поэтому для акционеров предприятия он является наиболее значимым. Критерием принятия проекта к реализации является положительное значение NPV при заранее заложенной ставке дисконтирования.

Внутренняя норма доходности (IRR) не зависит от ставки дисконтирования. Для ее расчета можно использовать компьютерные средства либо рассчитывать вручную методом подбора. Согласно правилу внутренней нормы доходности инвестиционный проект следует принять, если альтернативные издержки привлечения капитала меньше внутренней нормы доходности, то есть IRR > ?. Если альтернативные издержки равны внутренней норме доходности, то это проект с нулевым NPV.

При сравнении нескольких проектов более предпочтительными являются проекты с большими значениями IRR.

Индекс рентабельности PI должен быть больше 1, что означает привлекательность вложения инвестиций в проект. При рассмотрении нескольких проектов следует выбрать к реализации тот из них, который имеет наиболее высокий индекс рентабельности.

Срок окупаемости РР при оценке эффективности инвестиционного проекта выступает в качестве ограничивающего условия. В некоторых случаях используют систему классификации проектов, в которой период окупаемости указывает, насколько быстро каждый из проектов должен быть реализован.

Общественная эффективность OP для инвестиционного проекта является качественной оценкой, значение которой лежит в пределах от нуля до единицы. Наиболее значимые для общества инвестиционные проекты должны иметь значение ОР, близкое к единице. При определении этого следует учитывать возможные результаты от реализации проекта: выручка от реализации продукции, экологические и социальные результаты, финансовые результаты (налоги, амортизация, прибыль) и т.д. Здесь возможны три пути определения значений ОР:

– использование метода экспертных оценок Черчмена – Акофа;

– моделирование возможных значений ОР как многомерной случайной величины с известными законами распределения указанных компонент (социальные и экологические результаты, финансовые результаты, выручка от реализации продукции и т.д.);

– построение прогнозирующей функции [7].

Учитывая, что третий путь является классическим, остановимся только на двух первых.

Определение значений общественной эффективности методом экспертных оценок

Пусть имеется множество инвестиционных проектов

.

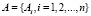Значение общественная полезность каждого из них обозначим через ОРi, i = 1,2,…,n.

Для определения конкретных значений ОРi, на основе метода измерения полезностей Черчмена-Акофа [1], построим следующий модифицированный алгоритм.

Шаг 1. Осуществляется упорядочивание нумерации проектов так, чтобы проект А1 был наиболее, а проект Аn – наименее предпочтительным. Следовательно, ОРi >ОРi+1, i = 1,2,…,n-1.

Шаг 2. Интервал [0,1] возможных значений ОР разбивается на n равных подынтервалов длиною ∆.

Шаг 3. На основе экспертных оценок проставляются знаки предпочтения в таблице Черчмена-Акофа

Шаг 4. Вычисляются предварительные оценки ОР по формуле

.

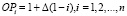Шаг 5. Подставляя найденные предварительные значения ОРi в неравенства таблицы Черчмена-Акофа в обратной последовательности корректируют нарушенные неравенства с минимальным шагом ∆/2. Полученные таким образом окончательные величины ОРi, i = 1,2,…,n и являются значениями общественной эффективности рассматриваемых проектов Аi, i = 1,2,…,n.

Моделирование возможных значений общественной эффективности

При наличии теоретических или полученных на основе статистических данных закономерностей изменений указанных выше компонент общественной эффективности можно смоделировать их возможные прогнозные величины и тем самым оценить предполагаемые значения общественной эффективности инвестиционных проектов.

Представим общественную эффективность ОР конкретного инвестиционного проекта в виде векторной случайной величины ОР = (Р1, Р2,…, Рm), где Рi – i-й компонент общественной эффективности, например Р1 – социальные результаты, Р2 – экологические результаты и т.д., а Fi(p) – законы распределения значений i-й компоненты.

Для оценки возможных значений общественной эффективности необходимо смоделировать случайные величины Рi, i = 1,2,…,n, т.е. найти их реализации рi по заданным законам распределения. При условиях, что законы распределения представлены простыми аналитическими зависимостями можно использовать метод обратной функции, основанный на утверждении [10]: «Случайная величина Р реализации р которой определяются из выражения

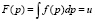или ,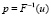

где u – случайные числа, равномерно распределенные в интервале [0, 1], имеет плотность распределения f(p)». Этот метод, не смотря на хорошее теоретическое обоснование, из-за необходимости решения интегрального уравнения имеет ограниченную область применения.

Для моделирования компонент Рi, i=1,2,…,n законы распределения которых представлены достаточно сложными аналитическими зависимостями, либо заданы в виде графиков или таблиц и наложено ограничение 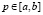можно применить метод исключения Джон фон Неймана, имеющего более прикладной характер [10].

Алгоритм моделирования компонент возможных значений общественной эффективности реализующий метод исключения Джон фон Неймана состоит из следующих шагов:

Шаг 1. Положить j = 1.

Шаг 2. Получить две независимые реализации u2j-1 и u2j случайной величины U .

Шаг 3. Вычислить

pj = a + u2j-1(b-a) и qj = M u2j.

Шаг 4. Проверить условие qj < f(pj). При его нарушении перейти на шаг 6.

Шаг 5. Принять P = pj .

Шаг 6. Положить j = j + 1.

Шаг 7. Вывод {pj}.

После определения таким образом возможных реализаций р всех компонент Рi , i = 1,2,…,n общественную эффективность эксперты оценивают значение ОР конкретного проекта.

Выбор инвестиционных проектов

Таким образом, множество инвестиционных проектов

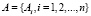
для каждого из его элементов вычислены приведенные выше показатели эффективности, образующие множество

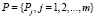
является объектов инвестиционного процесса. В свою очередь, Рj – это вектор размерности n.

Значения этих m показателей для рассматриваемых n инвестиционных проектов представим в виде матрицы

(1)

Применительно к показателям, рассмотренных в разделе 1, матрицу можно представить в виде таблицы данных (таблица).

Для выбора из множества проектов А одного или нескольких проектов с лучшими показателями можно воспользоваться классическими методами теории голосования (Парето, Борда, Кондорсе) [2]. С учетом того, что количество выбираемых проектов не всегда заранее задано, наиболее приемлемым в данном случае, по мнению авторов статьи, является метод Борда. Суть метода Борда состоит в определении результатов голосования в виде числа баллов, набранных каждым из кандидатов. Так, при выборах из n кандидатов каждый голосующий ранжирует всех кандидатов строго по убыванию предпочтения. За первое место по предпочтению кандидату присуждается n баллов, за второе n-1 баллов и т.д. (за последнее место – 1 балл), все набранные кандидатами баллы суммируются. Соответственно, победителем выборов считается кандидат, набравший наивысший суммарный балл.

Применительно к задаче выбора инвестиционных проектов, где не всегда возможно строгое ранжирование значений всех показателей, алгоритм этого метода можно построить в следующем виде:

Шаг 1. Пусть j = 1.

Шаг 2. Ранжирование элементов j-го столбца матрицы (1) по убыванию значений его элементов.

Шаг 3. Присвоение наивысшего ранга r = n первому элементу ранжированной последовательности, ранга r = n-1 следующему элементу последовательности и т.д. до завершения процедуры присвоения по признакам r = 1 или r = k, где k число элементов j-го столбца матрицы показателей одинаковых с любыми другими элементами данного столбца.

Шаг 4. Проверка условия j ≤ m. Если да, то на шаг 5, иначе на шаг 6.

Шаг 5. Вычисление j = j+1 и переход на шаг 2.

Шаг 6. Для каждого проекта Аi, i = 1,2,….n определение его ранга ri как суммарного значения по всем столбцам.

Шаг 7. Вывод результатов.

Полученные таким образом ранги инвестиционных проектов и являются основой для выбора подмножества В⊂A, включающего приемлемые для инвестирования проекты из исходного множества А.

Оптимизация объемов инвестирования

Для оптимизации объемов инвестиций по выбранным проектам рассмотрим случай распределения финансовых средств в объеме S, выделенных правительством для инновационного развития конкретных предприятий из K секторов экономики.

Формально задача банка развития может выглядеть следующим образом:

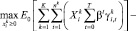
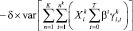(2)

при соблюдении следующих ограничений

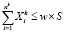
для всех секторов k = 1, 2,…,K (3)

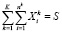(4)

В вышепоставленной задаче мы используем следующие обозначения:

1) 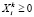– денежные инвестиции в компанию i из сектора k, где i = 1,2,…,nk;

2) 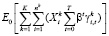это математическое ожидание всех будущих платежей, полученных от компаний-заемщиков в будущем с точки зрения периода 0;

3) 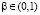– дисконтный фактор, который банк использует, чтобы оценивать платежи из последних кварталов;

4) Индекс T – максимальное количество кварталов, в течение которых, по крайней мере, какие-нибудь компании должны выплачивать займы (максимальный срок займов);

5) K – количество разных секторов. А число nk – это количество компаний из сектора k, проекты которых банк намеревается включить в свой портфель;

6) w – предельное значение доли средств, выделяемых в каждый из секторов;

7) 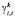– платеж компании i из сектора k в квартал t.

Задача (2-4) относится к классу нелинейных задач математического программирования с квадратичной целевой функцией и ее решение не представляет принципиальных затруднений в случае корректности ее постановки. В случае некорректности постановок или «возмущенности» параметров задачи для оптимального распределения объемов инвестиций можно воспользоваться методом расширения множества допустимых решений [10].

Заключение

В статье приведены взаимосвязанные модели и алгоритмы трех основных этапов прединвестиционной деятельности банка развития по анализу экономических показателей, выбору перспективных инвестиционных проектов и определению оптимальной стратегии распределения объемов инвестиций. Представленные модели и алгоритмы рассмотренных этапов, осуществляемых банком развития, являются достаточно универсальными и актуальны не только для реализации государственной стратегии в данном направлении, но и для осуществления коммерческих интересов любого банка в области инвестирования.

Библиографическая ссылка