Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Медведев А.В. 1

---

1 Кемеровский филиал Российского экономического университета им. Г.В. Плеханова

В статье предложен комплекс инструментов оперативной поддержки принятия решений в сфере анализа бизнес-проектов, состоящий из математической модели в форме задачи линейного программирования, описывающей деятельность производственного предприятия, а также модулей ее автоматизированного анализа, ввода и вывода информации. Модель позволяет находить оптимальные распределения инвестиций по видам основных производственных фондов, объемы производимой на них продукции, а также оптимальные значения внешних источников финансирования – кредитов и дотаций – с точки зрения максимизации чистой приведенной стоимости производственного предприятия, а также получать соответствующие показатели финансово-хозяйственной деятельности предприятия. Анализ модели осуществляется c использованием авторского оптимизационного пакета программ, а также модулей автоматизированной постобработки решения путем варьирования параметров бизнес-проекта и графической визуализация полученных зависимостей. Предложенный инструментарий позволяет осуществлять оперативную экспресс-оценку эффективности бизнес-проектов и применяется в действующем ситуационном центре регионального социально-экономического развития.

Статья в формате PDF

2612 KB

линейная модель оптимизации

оперативный анализ экономической эффективности

оптимизационный анализ финансово-хозяйственной деятельности

1. Горбунов М.А. Оптимизационный пакет прикладных программ «Карма» и его применение в задачах бизнес-планирования / М.А. Горбунов, А.В. Медведев, П.Н. Победаш, А.В. Смольянинов // Фундаментальные исследования. – 2015. – № 4. – С. 42-47.

2. Киренберг А.Г., Медведев А.В. К аппаратному обеспечению ситуационных центров социально-экономического развития // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 5-4. – С. 673-674.

3. Медведев А.В. Концепция оптимизационно-имитационного бизнес-планирования [Текст] / А.В. Медведев // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 1. – Ч. 2. – С.1 98-201.

4. Медведев А.В. Об эффективном инструментарии анализа экономических систем // Международный журнал прикладных и фундаментальных исследований. – 2014. – № 11(5). – С. 763-766.

5. Медведев А.В. Оптимизационная система поддержки принятия решений в бизнес-планировании // Успехи современного естествознания. – 2015. – № 1(4). – С. 679-683.

6. Медведев А.В., Трусов А.Н. К технологии поддержки региональных проектов развития в ситуационных центрах социально-экономического анализа // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 8-1. – С. 104.

7. Медведев А.В., Ухов А.С. К программному обеспечению ситуационных центров социально-экономического развития // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 5-4. – С. 674-675.

Уровень развития информационных технологий на сегодняшний день требует разработки адекватного инструментария для автоматизированной обработки информации в сфере социально-экономического анализа в режиме реального времени. К такому инструментарию следует отнести математические модели развития социально-экономических систем, алгоритмы расчета показателей и оценки эффективности их функционирования, позволяющие разрабатывать автоматизированные финансово-аналитические программные средства для принятия обоснованных управленческих решений. Распространение ситуационных центров экспертной поддержки принятия решений, используемых при анализе состояния, динамики развития территорий различного масштаба (стран, регионов, муниципальных образований и т.п.), производственных комплексов (предприятий, отраслей, направлений экономической деятельности региона и т.п.) делает решение соответствующего комплекса задач особенно актуальным. Учитывая широту встающих перед такими центрами задач социально-экономического характера, программное обеспечение для их решения должно быть сбалансировано по характеристикам адекватности используемых для описания социально-экономических процессов математических моделей, объемов входной информации, а также скорости обработки извлекаемой из моделей выходной информации. В частности, ряд информационных процессов (занесение, обработка, анализ, визуализация и т.п.) должны осуществляться в реальном режиме времени. При наличии экономико-статистической информации микроэкономического уровня (о функционировании предприятий, корпораций, а также решения задач финансовой поддержки малого и среднего бизнеса) актуальной остается разработка автоматизированных систем для анализа и оценки проектов развития бизнеса, эффективных способов его поддержки. В работах [3, 5] обоснована концепция оптимизационного моделирования и автоматизированной поддержки принятия решений для инвестиционных и производственно-финансовых проектов. Вместе с тем, вопросам анализа финансово-хозяйственного планирования деятельности экономических систем микроуровня (включая оптимизационный анализ потоков прибыли, амортизации, оплаты труда, налоговых и материальных затрат, решения задач текущей платежеспособности и т.п.) в современной литературе уделено недостаточно внимания. В данной работе представлены некоторые результаты исследований, связанных с решением вышеуказанных задач в их взаимоувязке с задачами разработки систем поддержки принятия оперативных, экспертных решений.

Для решения описанных задач рассмотрим автоматизированную информационную систему, описанную в [1], основанную на многокритериальной линейной модели оптимального управления и ее автоматизированном многопараметрическом анализе, и удовлетворяющую описанным выше требованиям к программному обеспечению ситуационных центров. Указанная система, в частности, позволяет осуществлять поддержку принятия решений по оптимальному распределению объемов производства, инвестиций, других финансовых ресурсов, анализу бизнес-проектов. За счет реализации в пакете решения стандартной математической задачи (многокритериальной задачи линейного программирования, МЗЛП) и наличия хорошо разработанного математического и численного инструментария (симплекс-метод, свертка критериев), модулей автоматизированной пред- и постобработки информации ее можно назвать удачным IT-решением, прошедшим неоднократную апробацию на реализуемых в настоящее время проектах микро- и мезоэкономического уровней.

Рассмотрим следующую содержательную постановку задачи. Деятельность производителя продукции n видов (товаров и/или услуг) описывается, выраженными в стоимостном виде, материальными и финансовыми потоками стратегического (прибыль, остаточная стоимость имущества, инвестиции) и тактического (выручка от продажи продукции, амортизация, фонд оплаты труда, налоги, оборотные затраты, кредиты, дотации и пр.) характера. При этом выполняется принцип «чистых отраслей»: на одном типе основных производственных фондов (ОПФ) производится один вид продукции. Указанная деятельность делится на три составляющие: инвестиционную (учет потоков, обусловленных приобретением (продажей) ОПФ, операционную (учет выручки, затрат на амортизацию ОПФ, оплату труда, сырья и материалов, энергии и т.п.) и финансовую (учет кредитов, налогов, сборов, дотаций и других доходно-расходных потоков, обеспечивающих финансирование (платежеспособность) производителя). Требуется определить в стоимостном виде оптимальные объемы приобретаемых ОПФ (инвестиций), выпуска продукции каждого вида, кредитов, дотаций, при которых дисконтированное сальдо доходов и расходов производителя за горизонт планирования T являются максимальными с учетом естественных ограничений на перечисленные составляющие его деятельности [5].

Отметим, что, при необходимости, нетрудно рассмотреть различные разновидности взаимодействия производителя с другими экономическими агентами (потребитель, налоговый центр, инвестор и пр.) для многокритериального анализа указанного взаимодействия [4]. Однако, в данной работе такая задача не ставится.

Для решения сформулированной выше задачи введем далее следующие обозначения:

n – количество видов продукции/ОПФ (ед.).;

k = 1,…,n – порядковый номер продукции/ОПФ;

сk – стоимость единицы k-го ОПФ (ден. ед/ед. ОПФ);

Pk – стоимость продажи единицы продукции k-го вида (ден. ед./ед. продукции);

Vk – производительность k-го ОПФ за период Т (ед. продукции/(ед. ОПФ));

Tk – время полезного использования k-го ОПФ (лет);

qk – спрос на продукцию, произведенную на k-м ОПФ, за период Т (ден. ед./ед. прод);

θk – стоимость всех видов сырья, использованного на производство k-й продукции (ден. ед./ед. пр.);

βk – доля выручки от продажи k-й продукции, выделяемая в фонд оплаты труда (ФОТ) (экспертный показатель трудоемкости производства);

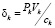– фондоотдача k-го ОПФ за период Т;

α_i, i = 1,…,4 – соответственно ставки налогов на добавленную стоимость, имущество, прибыль, страховых взносов в социальные фонды; α₅ – ставка других, зависящих от объемов производства, налоговых или неналоговых затрат;

Т – горизонт планирования, r – годовая ставка дисконтирования;

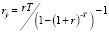– эффективная ставка дисконтирования проекта за период Т;

Т0 – срок кредита, r0 – годовая ставка кредита;

M0, Cr0, Dot0 – максимальные суммы инвестиций в ОПФ, кредитов и дотаций соответственно.

Пусть

x_k(k = 1,…,n) – стоимость всех приобретаемых ОПФ k-го вида за период Т, ден. ед.;

x _n+k(k = 1,…,n) – выручка от продажи всей продукции k-го вида за период Т, ден. ед.;

x _2n+1 – сумма кредита, взятого под обеспечение финансирования бизнес-проекта;

x _2n+2 – сумма дотаций предприятию за период Т.

Тогда, учитывая введенные обозначения, получим:

W = R – Z – балансовая прибыль предприятия за период Т (ден. ед.),

где 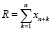– сумма выручки от продаж продукции k-го вида за период Т (ден. ед.);

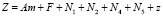– общие затраты производителя за период Т (ден. ед.);

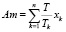– амортизационные отчисления за период Т (ден. ед.);

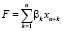– общий ФОТ за период Т (ден. ед.);

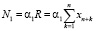– налог на добавленную стоимость за период Т(ден. ед.);

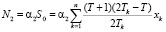– налог на имущество за период Т (ден. ед.);

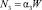– налог на прибыль стоимость за период Т (ден. ед.);

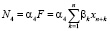– страховые взносы за период Т (ден. ед.);

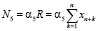– другие налоговые и неналоговые затраты за период Т (например, налог на добычу полезных ископаемых, экологические штрафы, «откаты» и пр.), зависящие от объемов производства (ден.ед.);

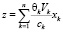– материальные (сырье, материалы и пр.) затраты производителя за период Т.

С учетом введенных обозначений, матричная форма математической модели, описывающей деятельность производственного предприятия, принимает следующий вид:

c _1×(2n+2) ·X _(2n+2)×1 → max, A _{(2n+4)×(2n+2)} ·X _(2n+2)×1 ≤ b _(2n+4)×1, (*)

А = ,

B = (0; Imax; 0,…,0; q1,…,qn; Crmax; Dotmax)T,

.

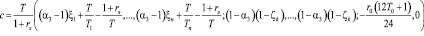
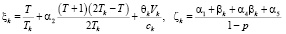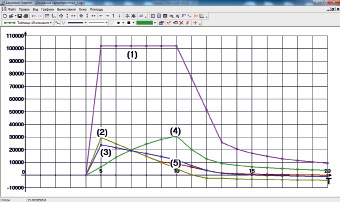
Рис. 1. Зависимости выручки (1), расчетной (2) и бухгалтерской (3) прибыли, NPV (4) и собственных средств производителя (5) от горизонта планирования Т

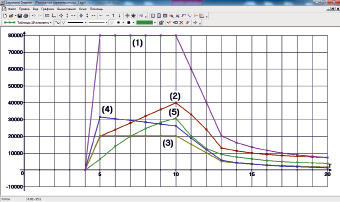
Рис. 2. Зависимости инвестиций (1), амортизации (2), ФОТ (3), налогов (4), NPV (5) от горизонта планирования Т

Модель (*) позволяет находить оптимальные распределения инвестиций по видам ОПФ, объемы производимой на них продукции, а также оптимальные значения внешних источников финансирования – кредитов и дотаций – с точки зрения максимизации чистой приведенной стоимости производственного предприятия. Анализ модели осуществляется c использованием оптимизационного пакета программ, подробно описанного в работе [1], в котором предусмотрена возможность выведения информации в среду Microsoft Excel. Исследовательским коллективом под руководством автора разработаны модули автоматизированной постобработки получаемой при анализе модели (*) информации, с использованием указанного пакета, в которых осуществляется автоматизированный расчет показателей финансово-хозяйственной деятельности предприятия путем варьирования соответствующих параметров, а также визуализация полученных зависимостей. На рис. 1, 2 изображены полученные с помощью модулей постобработки графики зависимостей от горизонта планирования Т оптимальных значений ряда параметров, характеризующих доходные (рис. 1) и расходные (рис. 2) характеристики некоторого бизнес-проекта.

Перечисленный инструментарий – математическая модель (*), программные модули автоматизированного внесения входной информации, оптимизационного многокритериального и многопараметрического анализа, постобработки выходной информации лежат в основе системы оперативной, экспертной поддержки принятия решений при анализе бизнес-проектов. Его существенной особенностью является возможность применения в условиях семинаров, мобильных заседаний экспертных групп, благодаря разработанному программному и аппаратному обеспечению [2, 6-7] ситуационного центра регионального социально-экономического развития Кемеровского института (филиала) Российского экономического университета имени Г.В. Плеханова.

Библиографическая ссылка