Постановка задачи многокритериального выбора оптимальной альтернативы действий непосредственно связаны с задачами многокритериальной оптимизации, содержание которых может быть определено следующим образом.
Для каждого объекта (проекта, минимизации затрат и т.п.) вводят вектор - критерий n¯ = {N1,N2,...,Nm}, в котором частный критерий Nj представляет функцию параметров a1, a2, an (которые определяют, например, характеристики управлений проектов и т.п.).
Функциональная зависимость частных критериев от параметров задачи задается и тогда основная математическая модель многокритериальной оптимизации будет сформулирована так:
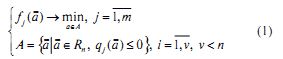
В этой модели A - допустимых решений, удовлетворяющих определенным ограничениям, аоторые даны в виде системы неравенств (a) < 0, накладываемых на вектор параметров a¯ = {A1, A2,..., An}.
Функция fj (A1, A2,...,An), будет называться j-той целевой функцией, а вся совокупность f1 (x¯),...,fm (x¯) образуют векторную целевую функцию многокритериальной оптимизации.
В принципе задача оптимизации может ставиться отдельно для частного критерия
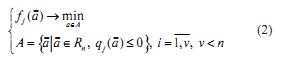
Задача (2) является скалярной задачей теории оптимизации, поэтому, одним из возможных приложений может служить задача о нормировании уровня загрязнений в промышленном центре.
Предположим, что уровень загрязнений воздушного бассейна в пределах индустриального центра определяется, по крайней мере, по одной из возможных компонент вредных веществ скалярной величиной
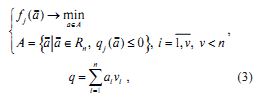
где vi - объем выбросов вредных веществ j-м предприятием района, bi - полный объем отходов на i-ом предприятии по данной компоненте загрязнений, ai - некоторые весовые коэффициенты (ai > 0). Зачастую в качестве последних берутся системы экологической вредности выбросов того или иного предприятия. Часть доходов, а именно (bi - vi) вырабатывается предприятием, и это связано с затратами
![]()
Если уровень загрязнений в районе превышает величину Q, то на предприятия накладываются штрафы Si (Si > 0). В результате функция затрат i-го предприятия записывается в виде:
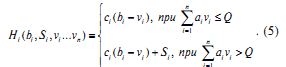
Каждое из предприятий заинтересованно в минимизации своих затрат. Центру предписана A0, следящая за уровнем загрязнений и предоставлено право ограничивать значения величин
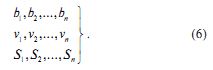
Критерии центра можно записать
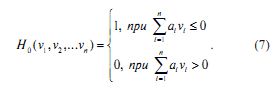
Целью центра является максимизировать целевую функцию (6) посредством соответствующего выбора b1, b2, ..., bп и S1, S2, Sn. В рассматриваемой системе оптимальным будет то состояние, при котором
H0 (v1,v2,vn) =1, и
![]()
Основной вопрос состоит в следующем: каким должно быть оптимальное управление V‾ (v1,v2,...vn). Отсюда ясно, что предприятия будут выбирать vi таким образом, чтобы меньше тратить средств на переработку, и вместе с тем ясно, что в целом в системе должна складываться ситуация, при которой
![]()
Условие (9) можно считать первым ограничением на вектор V(v1,v2,...vn). С учетом этого можно принять
![]()
и тогда решаемая оптимизированная задача примет вид
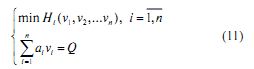
Поскольку целевые функции линейны и линейно также ограничение, то истинно попытаться свести задачу (11) к стандартной задаче линейного программирования используя в частности X - сверху векторного критерия H‾(V‾). Задача (11) можно сказать, таже эквивалентна задаче определения вектора V‾ из оптимизационной задачи вида
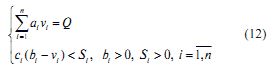
Особенностью структур систем является наличие ситуаций, в которых собственные цели подсистем не соответствуют в полной мере целям центра. Это ведет к так называемым конфликтам в системе. Такие ситуации изучаются на основе теоретико-игровых моделей.
Список литературы.
- Шапиро Д.И. Принятие решений в системе организационного управления. Исследование расплывчатых категорий. М.: Энергоато-миздат, 1983.
- Ларичев О.И. Наука и искусство принятия решений. М., 1979.
- Денисенко Т.И. Нелинейный вариант модели межотраслевого баланса, учитывающий вредные воздействия производства на окружающую среду. III Всероссийский симпозиум. г. Кисловодск, 1999.
Библиографическая ссылка
Денисенко Т.И. ПРОБЛЕМЫ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ // Международный журнал прикладных и фундаментальных исследований. 2010. № 12. С. 129-130;URL: https://applied-research.ru/ru/article/view?id=1024 (дата обращения: 15.02.2026).

