Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Тер-Акопянц Г.Л. 1 Тер-Акопянц Л.Г. 1

---

1 СПбГМТУ «Санкт-Петербургский Государственный морской технический университет»

В работе рассмотрено распространение упругих волн в цилиндрической оболочке, заполненной сжимаемой жидкостью, для неосесимметричных, осесимметричных и изгибных колебаний. Сопоставлены дисперсионные кривые для оболочки со сжимаемой жидкостью, для оболочки с несжимаемой жидкостью и для абсолютно жесткого цилиндрического волновода со сжимаемой жидкостью. Это позволило выявить волны преимущественно структурного и преимущественно жидкостного характера. Метод основан на том, что в оболочке, заполненной несжимаемой жидкостью, возможно распространение только структурных волн, а в жёстком волноводе, заполненном сжимаемой жидкостью, возможно распространение только жидкостных волн.

Статья в формате PDF

2756 KB

упругая цилиндрическая оболочка с жидкостью

распространение волн

дисперсионные кривые

осесимметричные колебания

изгибные колебания

1. Тер-Акопянц Г.Л. Дисперсионные кривые и модальные коэффициенты при распространении волн в оболочке с жидкостью // Естественные и технические науки. – 2015. – № 6(84). – C. 77-81.

2. Тер-Акопянц Г.Л. Осесимметричные волновые процессы в цилиндрических оболочках, заполненных жидкостью // Естественные и технические науки. – 2015. – № 7 (85). – С. 10-14.

3. Филиппенко Г.В. Анализ потоков энергии в бесконечной цилиндрической оболочке, контактирующей со сжимаемой жидкостью. XXVII сессия Российского акустического общества. Санкт-Петербург, 16-18 апреля 2014 г.

4. Fuller C.R., Fahy F.J. Characteristics of wave propagation and energy distributions in cylindrical elastic shells filled with fluid. // Journal of Sound and Vibration. – 1982. – № 81(4). – Р. 501-518.

5. Sarkar A., Sonti V.R., Asymptotic analysis for the coupled wavenumbers in an infinite fluid-filled flexible cylindrical shell: the axisymmetric mode. // Computer Modeling in Engineering and Sciences. – 2007. – № 21(3). – Р. 193–207.

6. Sarkar A., Sonti V.R. Asymptotic analysis for the coupled wavenumbers in an infinite fluid-filled flexible cylindrical shell: the beam mode. // Journal of Sound and Vibration. – 2009. – № 319. – Р. 646–667.

Целью работы является выявление из всего спектра упругих волн, распространяющихся в цилиндрической оболочке, заполненной сжимаемой жидкостью, волн преимущественно структурного и преимущественно жидкостного характера.

Следуя [4, 5, 6], будем искать решения системы динамических уравнений равновесия в перемещениях, учитывающей наличие жидкости внутри оболочки, в виде:

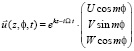, (1)

где z – продольная безразмерная координата, Ω – частота, k – приведённое осевое волновое число, m – фиксированное число окружных волн.

Выбор перемещений в виде (1) означает, что чисто мнимые значения k соответствуют распространяющимся волнам. Из пары волн, распространяющихся в противоположных направлениях, будем рассматривать только одну, распространяющуюся (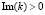) в направлении оси 0z.

Система уравнений для амплитуд перемещений в матричной форме принимает вид:

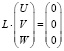, (2)

где

,

,

,

,

, ,

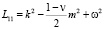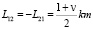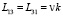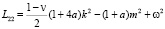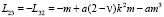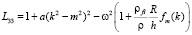ω – приведённая частота, 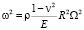, , 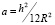ρ, ρfl – плотности оболочки и жидкости, h – толщина, R – срединный радиус оболочки, E, v – упругие константы.

«Жидкостная» компонента в L33 имеет вид при m ≥ 1:

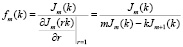для несжимаемой жидкости и

для сжимаемой,

где c, cfl – скорости звука в оболочке и в жидкости соответственно.

В частном случае осесимметричных колебаний m = 0:

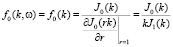
для несжимаемой жидкости,

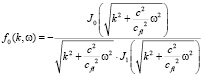
для сжимаемой жидкости.

Дисперсионные кривые для случаев осесимметричных m = 0 и изгибных колебаний m = 1 были показаны в работах [1] и [2]. Для сжимаемой жидкости они впервые получены, по-видимому, в [4].

Оболочка со сжимаемой жидкостью представляет собой единую двухкомпонентную систему, в которой нельзя рассматривать по отдельности волны в оболочке и волны в жидкости. Они всегда взаимосвязаны. Однако возможно выяснить за счет чего в большей мере распространяется волна (т.е. передается энергия), за счёт оболочки или за счёт жидкости, то есть подразделить распространяющиеся волны на волны преимущественно жидкостного и преимущественно структурного характера распространения.

Для получения этого нового результата сопоставляются дисперсионные кривые для оболочки со сжимаемой и с несжимаемой жидкостью. Волны, распространяющиеся в оболочке с несжимаемой жидкостью, исключительно структурные, так как в несжимаемой жидкости волны не распространяются. Поэтому на тех частотных интервалах, где дисперсионные кривые для оболочки со сжимаемой и с несжимаемой жидкостью совпадают, волна преимущественно структурная. Для выявления преимущественно жидкостных волн сопоставляются дисперсионные кривые для оболочки со сжимаемой жидкостью и для абсолютно жёсткого цилиндрического волновода со сжимаемой жидкостью, являющегося математической моделью оболочки очень большой жёсткости. В абсолютно жестком волноводе волны распространяются исключительно за счёт сжимаемой жидкости. Поэтому совпадение на некоторых частотных интервалах дисперсионных кривых в этом случае означает, что волна преимущественно жидкостная.

На рис. 1 представлены дисперсионные кривые для неосесимметричных режимов колебаний (m = 2 и m = 3).

Наблюдение за графиками показывает, что для этих двух режимов волна, описываемая красной дисперсионной кривой 1, всегда преимущественно структурная, а волна, описываемая синей дисперсионной кривой 2, всегда преимущественно жидкостная. Волна, описываемая розовой дисперсионной кривой 4, переходит на частоте ω = 2.15 при m = 2 и ω= 2.55 при m = 3 из преимущественно структурной в преимущественно жидкостную. Волна, описываемая голубой дисперсионной кривой 5, зарождается, как преимущественно жидкостная, но остаётся таковой только до частоты ω = 2.15 при m = 2 и ω = 2.55 при m = 3.

img src="/i/2016/10-2/terak1_fmt.jpg" alt="terak1.tif" />

Рис. 1. Дисперсионные кривые для неосесимметричных режимов колебаний

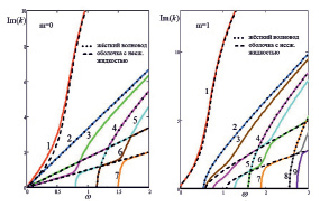
Рис. 2. Дисперсионные кривые для осесимметричных и изгибных колебаний

На рис. 2 представлены дисперсионные кривые для режимов осесимметричных колебаний (m = 0) и изгибных колебаний (m = 1).

Ввиду наибольшего практического интереса к этим двум режимам, результаты анализа дисперсионных кривых представим в табличной форме (табл. 1 и 2). Рассматривались частотные интервалы 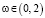для осесимметричного режима колебаний (m = 0) и 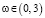для случая изгибных колебаний (m = 1).

Отметим, что в зонах сближения дисперсионных кривых (veering) как раз и происходит изменение механизма распространения волн и обмен энергией между оболочкой и жидкостью (см. [3]). Это особенно удобно проследить по правому рис. 2 для четвёртой распространяющейся волны (розовая линия), которая на частоте ω ≈ 1,8 переходит из преимущественно структурной в преимущественно жидкостную.

Практическое значение данного исследования в том, что колебания, передаваемые самой оболочкой (т.е. волны структурного происхождения), можно ослабить за счёт применения внешних устройств. Бороться с колебаниями, передаваемыми жидкостью, таким образом невозможно.

Таблица 1

Жидкостные и структурные волны в режиме осесимметричных колебаний

Таблица 2

Жидкостные и структурные волны в режиме изгибных колебаний

Выводы

Предложенный метод сопоставления дисперсионных кривых для оболочки со сжимаемой жидкостью, с несжимаемой жидкостью и для абсолютно жесткого волновода со сжимаемой жидкостью позволяет успешно определять, какие волны имеют преимущественно структурный, а какие преимущественно жидкостный механизм распространения.

Библиографическая ссылка