Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Меркухин Е.Н. 1

---

1 ФГБОУ ВО «Дагестанский государственный технический университет» Министерства образования и науки РФ

В статье предлагается метод синтеза тепловой модели, реализующей принцип суперпозиции температурных полей для платы, установленной в микроблоке электронной аппаратуры. Такая модель представляет интерес для задач оптимизации теплового режима путем рационального размещения интегральных схем, являющихся источниками тепла, так как она отражает их взаимное влияние друг на друга в явном виде. Это влияние определяется тепловыми коэффициентами, которые характеризуют степень влияния на температуру любой посадочной позиции интегральной схемы каждого из источников тепла, установленных на плате в позициях, предусмотренных ее конструкцией. Эти коэффициенты, согласно обоснованным допущениям, не зависят ни от температуры, ни от мощности источников тепла, а зависят исключительно от конструктивного исполнения платы. Предлагаемый метод определения коэффициентов влияния основан на проведении оптимального количества тепловых расчетов при наличии лишь одного источника тепла, перемещаемого последовательно в необходимые позиции. Полученная тепловая модель удобна для решения задачи оптимального размещения источников тепла методом ветвей и границ.

Статья в формате PDF

2020 KB

плата микроблока

тепловая модель

суперпозиция температурных полей

тепловые коэффициенты влияния

оптимальное размещение источников

1. Дульнев Г.Н. Тепло- и массообмен в радиоэлектронной аппаратуре: учебник для вузов по спец. «Конструирование и производство радиоаппаратуры». – М.: Высш. шк., 1984. – 247 с.

2. Лебедев Б.К., Меркухин Е.Н. Оптимизация тепловых характеристик при размещении элементов // Вопросы радиоэлектроники. Серия Электронная вычислительная техника. – Вып. 11. – 1988. – С. 186-194.

3. Меркухин Е.Н. Метод расчета теплового режима плат микроблоков электронной аппаратуры // Вестник Дагестанского государственного технического университета. Технические науки. – 2011. – Т. 21, № 2. – С. 32-36.

Обеспечение требуемого теплового режима является одной из важнейших задач проектирования электронных приборов. Для ее решения используются различные методы: применение элементной базы с меньшим тепловыделением, активные и пассивные методы охлаждения и рациональное размещение источников тепла. Последний метод особенно актуален для теплонагруженной аппаратуры, эксплуатируемой в условиях, когда ограничены возможности использования активных методов охлаждения и заданы жесткие требования на весогабаритные характеристики. В этом случае отвод тепла осуществляется преимущественно через элементы конструкции, и рациональное размещение источников тепла является одним из определяющих механизмов для улучшения теплового режима электронного аппарата.

В [2] предложен способ рационального размещения источников тепла в фиксированные позиции на плате с применением метода ветвей и границ. При этом используется тепловая модель на основе принципа суперпозиции температурных полей [1]:

,

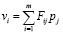где vi – перегрев i-той части системы относительно окружающей среды; Fij – тепловой коэффициент влияния j-той области на i-тую; pj – мощность, рассеиваемая j-той областью системы; m – число характерных областей, из которых состоит система. В качестве системы выбрана плата, а областями являются посадочные позиции, имеющие мощности рассеивания установленных в них источников тепла, представляющих собой интегральные схемы. При этом предполагается, что тепловые коэффициенты влияния определены и не рассмотрен вопрос их нахождения, так как это отдельная задача.

Цель исследования

В данной работе предлагается способ вычисления тепловых коэффициентов влияния, которые согласно обоснованным допущениям, не зависят ни от температуры, ни от мощности источников тепла, а зависят исключительно от конструктивного исполнения системы. При этом основная идея заключается в проведении оптимального количества тепловых расчетов при наличии лишь одного источника тепла, перемещаемого последовательно в необходимые позиции.

Материалы и методы исследования

В качестве инструментального средства использована подсистема расчета тепловых режимов микроблоков электронной аппаратуры [3].

Тепловые коэффициенты удобно задать в виде матрицы:

(1)

Физический смысл коэффициентов Fii | i = 1,2,…, m (F11, F22, F33 …Fmm) – тепловое сопротивление между i-той позицией для установки источника тепла и окружающей средой (теплостоком). Коэффициенты Fij| i = 1,2,..,m; j = 1,2,..,m; i ≠ j – отражают степень влияния источника тепла, установленного в j-тую позицию, на перегрев i–той позиции относительно окружающей среды, то есть величина произведения F_ij×p_j определяет наведенный перегрев в i-той позиции от источника тепла, установленного в j-тую позицию и имеющего мощность pj. Все тепловые коэффициенты имеют размерность теплового сопротивления – [градус/ватт].

Если установить на плату только один источник тепла в позицию k∈{1,2,…,m}, и провести расчет теплового режима, то мы получим наведенные перегревы во всех позициях, где нет источников тепла и собственный перегрев в позиции k, где установлен источник тепла. Это позволяет нам вычислить тепловые коэффициенты влияния k-той позиции Fik| i = 1,2,…,m на все остальные, в том числе и на саму себя (F1k, F2k,…,Fkk,…,Fmk):

;

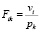где vi – перегрев i-той позиции.

В общем случае для определения всех тепловых коэффициентов требуется провести m расчетов тепловых режимов, перемещая источник тепла каждый раз в следующую позицию. Но так как в реальных конструкциях электронных аппаратов обычно имеет место симметрия теплоотвода, то количество тепловых расчетов можно существенно сократить. Более детально предлагаемый метод можно продемонстрировать на конкретном примере.

Проведем расчеты для определения тепловых коэффициентов влияния для печатной платы, установленной в корпусе микроблока и имеющей 24 фиксированные посадочные позиции для установки одногабаритных микросхем. Пронумеруем посадочные позиции, как показано на рис. 1. Для упрощения вычислений мощность перемещаемого по позициям источника тепла примем равной 1 ватту. Учитывая условие, что тепловая энергия отводится от микросхем через плату радиально, симметрично и преобладает кондуктивный механизм отвода, можно сократить количество тепловых расчетов до 6. Достаточно провести расчеты при нахождении источника тепла в позициях: 1, 2, 3, 7, 8, 9. В силу симметрии источник, расположенный в позиции 1 будет влиять на температуру позиции 7 так же, как источник, расположенный в позиции 19 будет влиять на температуру позиции 13. То есть будут иметь место следующие равенства:

F1,7 = F19,13 = F6,12 = F24,18; F2,8 = F20,14 = = F5,11 = F17,23;…и т.д.; (2)

F1,1 = F19,19 = F24.24 = F6,6; F7,7 = F13,13 = = F11,11 = F17,17… и т.д.

Рис. 1. Нумерация посадочных позиций на плате

Таким образом, установив источник тепла в позицию 1 и проведя тепловой расчет, получим значения перегревов во всех позициях, которые численно равны коэффициентам влияния источника тепла в первой позиции на все остальные, включая и первую, так как мощность источника тепла равна 1 ватту. С учетом равенств (2 ) в матрице (1) можно заполнить столбцы 1, 6, 19, 24. Расчеты теплового режима при установке источника в следующие позиции 2, 3, 7, 8, 9 позволят соответственно заполнить столбцы в матрице (1): (2, 5, 20, 23); (3, 4, 21, 22); (7, 12, 13, 18); (8, 11, 14, 17); (9, 10, 15, 16).

Таблица 1

Исходные данные для микроблока

Таблица 2

Исходные данные для платы

Таблица 3

Исходные данные для платы

Исходные данные для расчета теплового режима, когда источник установлен в позицию 1, приведены в табл. 1, 2 и 3.

Условные обозначения в исходных данных для микроблока и платы:

KONT – вариант теплоотвода от плат (KONT = 1 – с четырех сторон); NV – вариант ориентации плат в микроблоке (NV = 1 – горизонтальное расположение плат); TC – температура окружающей среды; PP – коэффициент перфорации корпуса микроблока; NN – число плат в микроблоке; D – толщина стенок корпуса микроблока; G – масса микроблока; C – удельная теплоемкость материала микроблока; B1 – высота корпуса микроблока; B2, B3- размеры основания микроблока; Alk – коэффициент конвективной теплоотдачи с поверхности микроблока; UT – коэффициент теплопроводности корпуса микроблока; EK – степень черноты корпуса; RTK – удельное тепловое сопротивление контакта «микроблок-теплосток»; H – расстояние от основания микроблока до платы (при NV = 1); K1, K2 – количество элементов с первой и со второй стороны платы, соответственно; IO – количество сквозных отверстий в плате; IT – количество теплопроводных шин на плате; XM – больший размер платы; YM – меньший размер платы; RT – удельное тепловое сопротивление контакта «плата-стенка микроблока»; HK – ширина контакта «плата-стенка микроблока»; DX – шаг разбиения платы на дискретное поле; DZ1 – толщина теплопроводного сердечника платы; DZ2 – толщина диэлектрического покрытия теплопроводного сердечника платы; DK1 – толщина клея между диэлектрическим покрытием и теплопроводным сердечником; DK2 – толщина пасты между диэлектрической платой и элементами на ней; ERRmax – максимальная относительная ошибка расчета теплового поля платы при которой этот расчет прекращается; UT1 – коэффициент теплопроводности теплопроводного сердечника платы; UT2 – коэффициент теплопроводности диэлектрического покрытия теплопроводного сердечника платы; UTK1 – коэффициент теплопроводности клея между диэлектрическим покрытием и теплопроводным сердечником; UTK2 – коэффициент теплопроводности пасты между диэлектрической платой и элементами на ней; Qmax – макс. число итераций расчета теплового поля платы; Alk1, Alk2 – коэффициенты средней конвективной теплоотдачи от элементов стоящих соответственно с первой и второй стороны платы; X, Y – координаты центра элемента стоящего на плате по осям X и Y; BX, BY – размеры элемента стоящего на плате по осям X и Y; мощность – мощность тепловыделения элемента; элемент – условное обозначение элемента.

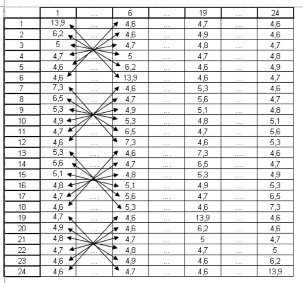
Рис. 2. Заполнение матрицы F

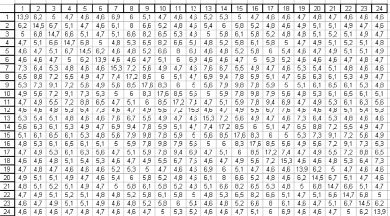
Рис. 3. Полностью заполненная матрица F

Результаты исследования и их обсуждение

Результаты расчета перегревов посадочных мест под микросхемами, которые численно равны тепловым коэффициентам влияния, (так как мощность тепловыделения микросхемы в первой позиции равна 1 ватту) занесены в первый столбец матрицы F, изображенной на рис. 2.

Первый столбец отражает распределение перегревов по посадочным позициям, когда источник установлен в первую позицию. Согласно равенствам (2) заполнены столбцы 6, 19 и 24. Принцип заполнения показан стрелками для 6-го столбца. По аналогии, согласно (2) заполнены столбцы 19 и 24.

На рис. 3 приведена полностью заполненная матрица F по результатам шести расчетов.

Полученная тепловая модель является частной. Она годится также для расчета тепловых режимов при неизменных конструктивных и теплофизических характеристиках. Но эта модель предназначается для решения оптимизационной задачи по рациональному размещению источников тепла, описанной в [2]. Для такой задачи можно провести нормирование матрицы, поделив все значения на максимальное число, содержащееся в ней. В работе [2] использовалась нормированная матрица F.

Заключение

Проведенные исследования, подкрепленные конкретным примером, показали, что, имея в распоряжении подсистему расчета теплового режима, можно за приемлемое время синтезировать тепловую модель на основе принципа суперпозиции температурных полей, которая наиболее удобна для решения задачи оптимального размещения источников тепла.

Библиографическая ссылка