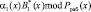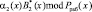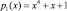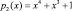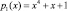В настоящее время наблюдается повышенный интерес разработчиков к блочным симметричным шифрам, которые используют подстановочно-перестановочную сеть (Substitution-Permutation Network). Такие шифры относятся к SPN-шифрам. В отличие от DES и ГОСТ 28147-89 эти шифры не используют сеть Фейстеля, а реализуют в одном раунде нелинейные и линейные преобразования, а также операцию наложения ключа. В результате этого в отличие от сети Фейстеля, при использовании SP-сети преобразуется весь входной блок, а не его половина. Однако в процессе работы шифратора SPN-шифров могут возникнуть сбои оборудования. Такие сбои могут быть результатом деструктивных воздействий как природного, так и антропогенного характера. Это приведет к искажению результата зашифрования.
Цель исследования
Повысить надежности работы SPN-шифрсистем можно за счет применения различных способов введения струтурной или временной избыточности. Однако известные способы противодействия последствиям сбоев в работе шифратора не учитывают особенности SPN-шифров, что приводит к значительным затратным схемным решениям. Решить данную проблему можно за счет использования избыточных кодов, которые реализованы, как и SPN-шифры, в алгебраической системе, обладающей свойством кольца и поля. Поэтому целью работы является повышение надежности SPN-шифров за счет применения избыточных кодов полиномиальной системы классов вычетов (ПСКВ) с минимальной избыточностью, способных обнаруживать ошибки, вызванные сбоями.
Материалы и методы исследования
Основу кодов ПСКВ составляет непозиционная система счисления, в которой в качестве оснований модулярного кода используются неприводимые полиномы pi(z). Произведение оснований кода ПСКВ позволяет определить рабочий диапазон
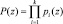 . (1)
. (1)
Тогда полином A(z), удовлетворяющий условию 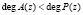 , можно представить в виде кортежа остатков
, можно представить в виде кортежа остатков
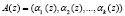 , (2)
, (2)
где 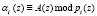 ; i = 1, 2, …, n.
; i = 1, 2, …, n.
Так как операции сложения, вычитания и умножения по модулю можно свести к соответствующим операциям над остаткам [4, 5, 8], то для кода ПСКВ имеет место равенство
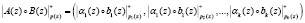 , (3)
, (3)
где 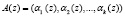 ;
;
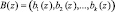 ;
;  – модульная операция.
– модульная операция.
Для выполнения процедур обнаружения ошибки в код ПСКВ вводят минимальную избыточность – одно контрольное основание, которое удовлетворяет
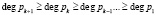 . (4)
. (4)
В результате происходит расширение рабочего диапазона до полного диапазона
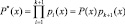 . (5)
. (5)
Тогда условием отсутствия ошибки в кодовой комбинации кода ПСКВ является выполнение неравенства
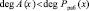 . (6)
. (6)
В противном случае получаем, что в коде ПСКВ произошла ошибка.
Для выполнения процедуры обнаружения ошибки в коде ПСКВ используют позиционные характеристики (ПХ) [2, 3, 6, 7]. В работе [1] приведен алгоритм вычисления данной позиционной характеристики – след полинома. Для получения конечного результата предлагается из исходного кода ПСКВ 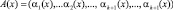 последовательно вычитать константы нулевизации до тех пор, пока не получится код
последовательно вычитать константы нулевизации до тех пор, пока не получится код
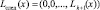 . (7)
. (7)
При этом подбираются специальные константы нулевизации, так чтобы при выполнении данного итерационного алгоритма не было бы ни один выхода за пределы рабочего диапазона системы Полученное значение (7) называется следом числа.
Проведенный анализ позволил выявить основной недостаток метода вычисления данной позиционный характеристики, который был приведен в работе [1]. Он связан с последовательным характером вычислительного процесса. Для устранения данной проблемы был разработан алгоритм параллельного вычисления позиционной характеристики – след полинома. Для этого предлагается заменить константы нулевизации Mi(z) на псевдоортогональные полиномы 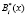 . Тогда получаем
. Тогда получаем
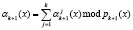 . (8)
. (8)
В этом случае нормированный след полинома можно получить путем вычитания из кода ПСКВ полинома A(x) псевдоортогональных форм, то есть
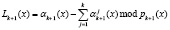 . (9)
. (9)
Если значение нормированного следа полинома равно нулю, то исходный код ПСКВ является разрешенным. В противном случае произошло обнаружение ошибки.
Результаты исследования и их обсуждение
Рассмотрим применение разработанного метода для повышения надежности AES-шифрсистем. Шифр AES реализуется в GF(28) с использованием 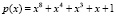 . Предлагается вместо него использовать код ПСКВ с двумя рабочими основания
. Предлагается вместо него использовать код ПСКВ с двумя рабочими основания 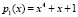 и
и 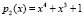 . В качестве контрольного основания применяем
. В качестве контрольного основания применяем 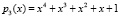 .
.
Для получения псевдоортогональных базисов вычислим ортогональные базисы для рабочих оснований. Тогда первый ортогональный базис 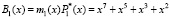 .
.
Значение второго ортогонального базиса 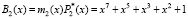 . Произведем расширение ПСКВ, добавляя в набор оснований контрольное основание.
. Произведем расширение ПСКВ, добавляя в набор оснований контрольное основание.
Таблица 1
Значение 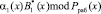
|
Остаток |
Произведение |
|
α1(x) = 1 |
(1, 0, х3 + 1) |
|
α1(x) = x |
(х, 0, х2 + 1) |
|
α1(x) = x2 |
(х2, 0, х + 1) |
|
α1(x) = x3 |
(х3, 0, х2 + х) |
Таблица 2
Значение 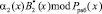
|
Остаток |
Произведение |
|
α2(x) = 1 |
(0, 1, х3) |
|
α2(x) = x |
(0, х, х2 + х) |
|
α3(x) = x2 |
(0, х2, х2 + 1) |
|
α2(x) = x3 |
(0, х3, х3 + х) |
Таблица 3
Таблица замен S1-блока по модулю 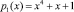
|
s2(x) |
Остаток s1(x) по модулю |
|||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
9 |
9 |
2 |
F |
D |
B |
B |
5 |
B |
F |
0 |
1 |
4 |
3 |
F |
9 |
|
1 |
D |
5 |
9 |
0 |
9 |
3 |
4 |
A |
4 |
F |
6 |
0 |
4 |
8 |
9 |
1 |
|
… |
||||||||||||||||
|
F |
1 |
5 |
3 |
3 |
6 |
B |
C |
7 |
1 |
A |
E |
C |
9 |
9 |
A |
F |
Таблица 4
Таблица замен S2-блока по модулю 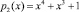
|
s2(x) |
Остаток s1(x) по модулю |
|||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
7 |
F |
8 |
3 |
5 |
C |
B |
8 |
6 |
4 |
5 |
4 |
E |
B |
C |
B |
|
1 |
B |
1 |
4 |
6 |
D |
9 |
B |
F |
D |
F |
A |
1 |
6 |
B |
C |
2 |
|
… |
||||||||||||||||
|
F |
7 |
F |
8 |
3 |
5 |
C |
B |
8 |
6 |
4 |
5 |
4 |
E |
B |
C |
B |
Затем произведем вычисление остатков ортогональных базисов по модулю контрольного основания. Получаем для первого ортогонального базиса
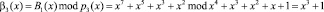 .
.
Для второго ортогонального базиса получаем
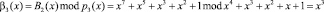 .
.
Тогда получаем два псевдоортогональных базиса
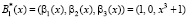 ;
;
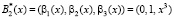 .
.
Вычислим значения, которые получаются при умножении псевдоортогональных базисов на остатки. Для первого модуля ПСКВ результаты приведены в табл. 1.
Для второго модуля ПСКВ результаты приведены в табл. 2.
Рассмотрим пример применения кода ПСКВ, обнаруживающего однократные ошибки. Пусть на входы S-блока поступает байт текущего состояния. При этом старшие 4 разряда байта определяют номер строки таблицы, а младшие 4 разряда – задают номер столбца. Так при подаче состояния {00011001} = {1916} на выходе S-блока будет результат {d416} = {110101002}, который находится на пересечении 1 строки и 9 столбца.
Рассмотрим применение избыточного кода ПСКВ, способного обнаружить ошибки, при работе S-блока. Пусть на вход S-блока поступил двоичный входной вектор S(x) = {000110012} = {1916}. Данное значение подается на вход прямого преобразователя ПСС-ПСКВ, на выходе которого будут
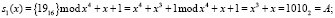
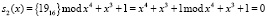
На входы таблиц замены S1-блока по модулю 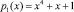 и S2-блока по модулю
и S2-блока по модулю 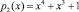 поступают остатки S(x) = (А, 0). Результат замены определяется из табл. 3 и 4. В табл. 3 показана таблица S1-блока по рабочему модулю
поступают остатки S(x) = (А, 0). Результат замены определяется из табл. 3 и 4. В табл. 3 показана таблица S1-блока по рабочему модулю 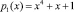 .
.
В табл. 4 показана таблица замен S2-блока по рабочему модулю 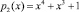 .
.
Для обнаружения последствий сбоев в шифре AES вводим таблицу S3. Табл. 5 содержит строки таблицы замен S3-блока по модулю 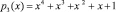 .
.
В табл. 3 на пересечении столбца А и строки 0 находится число 0. В табл. 4 на пересечении столбца А и строки 0 находится число 5. В результате воздействия байта состояния S(x) = {000110012} = {1916} = (А, 0) был получен байт подстановки, который в ПСКВ равен S’(x) = (0, 5). Это соответствует подстановке S’(x) = {d416} = {110101002}, так как
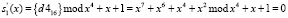 ;
;
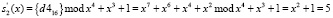 .
.
Определим остаток полученного значения подстановки S’(x) = {d416} = {110101002} по контрольному модулю. Тогда получаем
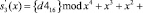
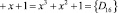 .
.
При подаче на вход табл. 3 значений остатков текущего блока S(x) = (А, 0) с выхода третьей таблицы подстановки будет снято значение, равное {D16} = {11012} = = {x3 + х2 + 1}. Данное число находится на пересечении столбца А и строки 0 в табл. 3.
Полученные значения остатков нового блока S’(x) = (0, 5) = (0, х2 + 1) поступают на первый вход блока обнаружения ошибки. Блок обнаружения ошибок реализует вычисление остатка по контрольному основанию, используя значение остатков S’(x) = (0, 5).
При использовании разработанного метода получили остатки:
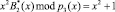 ;
;
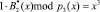 .
.
Тогда, просуммировав остатки по контрольному основанию, получаем
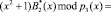
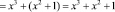 .
.
Одновременно с этим на второй вход блока обнаружения ошибки поступает значение 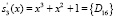 , которое было получено с выхода табл. 5. В результате этого получается, что след полинома равен нулю. Это означает, что ошибки в коде ПСКВ нет.
, которое было получено с выхода табл. 5. В результате этого получается, что след полинома равен нулю. Это означает, что ошибки в коде ПСКВ нет.
Пусть ошибка из-за сбоя произошла по второму основанию ПСКВ 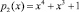 и ее глубина
и ее глубина 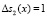 . Тогда
. Тогда
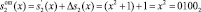 .
.
Тогда на вход блока обнаружения ошибок, буде подан код из двух остатков ПСКВ
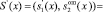
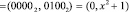 .
.
Проведем расчет остатка по контрольному основанию 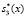 с помощью псевдоортогональных базисов. В вычисление данного остатка принимает участие полином
с помощью псевдоортогональных базисов. В вычисление данного остатка принимает участие полином
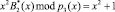 .
.
Тогда, просуммировав остатки по контрольному основанию, получаем
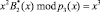 .
.
Одновременно с этим на второй вход блока обнаружения ошибки поступает значение 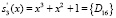 , которое было получено с выхода табл. 5. Тогда нормированный след полинома будет равен
, которое было получено с выхода табл. 5. Тогда нормированный след полинома будет равен
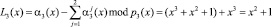 .
.
Таблица 5
Остатки 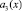 по модулю
по модулю 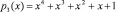
|
s2(x) |
Остаток s1(x) по модулю |
|||||||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
|
|
0 |
0 |
A |
E |
0 |
7 |
0 |
B |
2 |
C |
B |
D |
C |
8 |
9 |
1 |
F |
|
1 |
E |
0 |
E |
3 |
C |
F |
5 |
7 |
6 |
F |
9 |
8 |
2 |
6 |
4 |
F |
|
… |
||||||||||||||||
|
F |
0 |
F |
8 |
2 |
C |
5 |
D |
1 |
6 |
5 |
2 |
2 |
9 |
8 |
A |
A |
Полученный результат свидетельствует о том, что избыточный код ПСКВ содержит ошибку. Однако по величине данной позиционной характеристики определить местоположение ошибки нельзя.
Заключение
В работе проведена разработка и исследование новых принципов построения избыточных кодов полиномиальной системы классов вычетов, позволяющих обнаруживать ошибки на основе вычисления позиционной характеристики нормированный след. Показана возможность использования разработанного алгоритма вычисления данной ПХ для обнаружения ошибок, возникающих в процессе работы криптосистемы AES. Проведенные исследования показали, что применение разработанного алгоритма позволяет вычислить ПХ за одну итерацию по сравнению k итерациями вычисления следа числа, приведенных в работе [1], что значительно снижает временные затраты на обнаружение ошибки.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-50081.
Библиографическая ссылка
Бабенко Л.К., Калмыков М.И., Топоркова Е.В., Васильев В.А. РАЗРАБОТКА АЛГОРИТМА ОБНАРУЖЕНИЯ ОШИБОК В SPN-ШИФРСИСТЕМАХ НА ОСНОВЕ ИСПОЛЬЗОВАНИЯ ИЗБЫТОЧНЫХ МОДУЛЯРНЫХ КОДОВ // Международный журнал прикладных и фундаментальных исследований. 2016. № 11-2. С. 183-187;URL: https://applied-research.ru/ru/article/view?id=10461 (дата обращения: 03.03.2026).