Современные специализированные вычислительные системы имеют достаточно сложную структуру. Стремление обеспечить обработку данных в реальном масштабе времени привело к активизации работ по применению параллельных методов. Особенно это наглядно проявляется при реализации алгоритмов и методов цифровой обработки сигналов [3, 5, 7, 9]. Все это приводит к снижению надежности работы таких устройств. Поэтому обеспечение устойчивости к отказам, возникающим в процессе работы специализированых процессоров, является актуальной задачей. При этом необходимо выбрать такой вариант решения проблемы, который бы позволил реализовать процедуру коррекции ошибок при меньших схемных и временных затратах. Одним из перспективных путей решения этой проблемы является использование кодов полиномиальной системы классов вычетов (ПСКВ), способных обнаруживать и корректировать ошибки [5, 9].
Цель исследования
Сохранение работоспособного состояния параллельных вычислительных устройств во многом определяется быстротой и точностью определения местоположения и глубины ошибки. При этом предпочтение отдается информационной, а не технологической надежности системы, которая может быть достигнута путем специального кодирования, обеспечивающего обнаружение ошибок, возникающих в результате сбоев и отказов, и их исправление.
Поэтому целью работы является разработка метода коррекции ошибок, который на основе многоверсионной избыточности, позволил бы повысить отказоустойчивость спецпроцессоров ЦОС при меньших схемных затратах чем метод маскирования отказов «2 из 3».
Материалы и методы исследования
В коде ПСКВ в качестве оснований непозиционной системы используются неприводимые полиномы pi(z) – неприводимые полиномы поля GF(2); i = 1,…, k. Данный код относится к непозиционным кодам классов вычетов. В кодах ПСКВ берется сначала позиционный двоичный код А = 1101…12. Затем он представляется в полиномиальной форме в виде
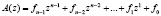 , (1)
, (1)
где 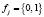 – элемент поля GF(2).
– элемент поля GF(2).
Используя полученную полиномиальную форму, определяются соответствующие остатки, полученные при делении полинома A(z) на основания ПСКВ. В результате получается набор остатков
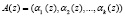 , (2)
, (2)
где 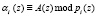 .
.
Произведение оснований кода ПСКВ позволяет определить рабочий диапазон
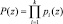 . (3)
. (3)
Проведенный анализ работ [2, 7, 9] показал, что наиболее эффективно выполняются в кодах ПСКВ модульные операции. К этим операциям относятся – сложение, вычитание и умножение по модулю. Пусть даны два полинома 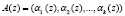 и
и 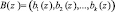 . Так как сравнения по одному и тому же модулю можно почленно складывать, то для модульных операций имеем
. Так как сравнения по одному и тому же модулю можно почленно складывать, то для модульных операций имеем
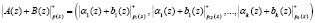 , (4)
, (4)
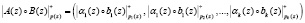 , (5)
, (5)
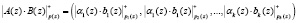 . (6)
. (6)
где + – операция суммирования по модулю р;  – операция вычитания по модулю р.
– операция вычитания по модулю р.
Одной особенностью модулярных кодов является их способность корректировать ошибки, возникающие в процессе вычислений. Для этого в состав модулярных кодов вводят дополнительно контрольных оснований ПСКВ из условия
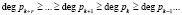 . (7)
. (7)
В результате применения контрольных оснований ПСКВ происходит расширение рабочего диапазона до полного диапазона
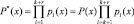 . (8)
. (8)
Так как ошибка переводит правильный 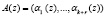 в ошибочный полином
в ошибочный полином 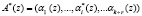 , лежащий вне рабочего диапазона, то, зная местоположение искаженного полинома A*(z), можно однозначно определить модуль pi(z), по которому произошла ошибка, а также ее глубину.
, лежащий вне рабочего диапазона, то, зная местоположение искаженного полинома A*(z), можно однозначно определить модуль pi(z), по которому произошла ошибка, а также ее глубину.
Независимая и параллельная обработка остатков по основаниям ПСКВ служат основой для использования многоверсионной избыточности для коррекции ошибок, возникающих из-за сбоев в работе системы. В отличие от позиционных помехоустойчивых кодов, которые применяют единый алгоритм вычисления синдрома ошибки, модулярные коды характеризуются многоверсионным подходом к обнаружению и коррекцию ошибок.
Так коды ПСКВ являются непозиционными, то для обнаружения местоположения и глубины ошибки используют позиционные характеристики (ПХ). Все множество методов коррекции ошибок можно разделить на две группы, в зависимости от используемой многоверсионной избыточности кодов ПСКВ. К первой относятся методы и алгоритмы контроля и коррекции ошибок непозиционного кода ПСКВ, базирующиеся на вычисление позиционных характеристик во временной области [1, 4, 5]. Что касается процедур второй группы, то они реализуются в частотной области [4]. Рассмотрим методы обнаружения и коррекции ошибок, работающие во временной области. В настоящее время широкое применение нашли такие методы вычисления ПХ как, интервальный номер, нормированный след, параллельная нулевизация, вычисление старших коэффициентов обобщенной полиадической системы. Наличие такой многоверсионной избыточности модулярных кодов позволяет разработчикам обоснованно выбирать соответствующий метод коррекции ошибок, исходя из заданных требований к вычислительным системам [8, 10].
Анализ известных методов контроля и коррекции ошибки в модульных избыточных кодах показал, что довольно часто поиск и исправление ошибок производится с помощью перевода чисел из модулярного кода в обобщенную полиадическую систему (ОПС) [4, 6]. Данные алгоритмы, основаны на вычисление коэффициентов промежуточной полиадической системы, в котором А(z) изображается в виде
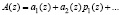
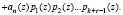 (9)
(9)
Если 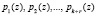 , служат одновременно основаниями модульной системы и ОПС, тогда интервалы изменения цифр разрядов с одинаковыми номерами совпадут. Следовательно, если обеспечить соответствие между основаниями ОПС и основаниями системы классов вычетов, то справедливо
, служат одновременно основаниями модульной системы и ОПС, тогда интервалы изменения цифр разрядов с одинаковыми номерами совпадут. Следовательно, если обеспечить соответствие между основаниями ОПС и основаниями системы классов вычетов, то справедливо
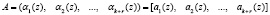 . (10)
. (10)
Исходя из условия, что 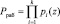 , выражение (9) имеет вид
, выражение (9) имеет вид
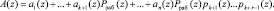 (11)
(11)
Тогда на основании (11) можно сделать вывод о возможности применения коэффициентов ОПС для процедур поиска и локализации ошибки. Данный вывод основывается на том, что, начиная с k + 1-го коэффициента ОПС, в слагаемых равенства (11) в качестве сомножителя используется Рраб(z). Таким образом, если полином А(z) принадлежит рабочему диапазону Рраб(z), то старшие коэффициенты ОПС должны 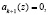
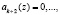
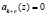 . В противном случае полином А(z) содержит ошибку и находится вне Рраб(z) кода ПСКВ.
. В противном случае полином А(z) содержит ошибку и находится вне Рраб(z) кода ПСКВ.
Особенностью разработанного методы состоит в том, что наиболее трудоемкий этап перевода остаток – коэффициенты ОПС осуществляется путем параллельно-конвейерного вычисления коэффициентов с использованием китайской теоремы об остатках [6]. Тогда
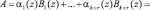
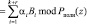 , (13)
, (13)
где Bi(z) – ортогональный базис i-го основания.
Представив ортогональные базисы в виде коэффициентов ОПС, получаем
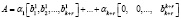 , (14)
, (14)
где 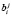 – коэффициенты ОПС j-го ортогонального базиса.
– коэффициенты ОПС j-го ортогонального базиса.
Тогда, проведя умножение вычетов αi на соответствующие коэффициенты ОПС помодульно и поразрядно, при этом, учитывая превышение модуля pi как перенос единицы при суммировании результата, коэффициенты ОПС могут быть найдены выражения
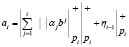 , (15)
, (15)
где ηi–1 – переполнение, полученное при суммировании по модулю pi–1.
Важнейшим из свойств кодов ПСКВ, является отсутствие межразрядных переносов при вычислении результата по модулю pi(z). Это позволяет свести операцию итеративного получения коэффициентов обобщенной полиадической системы к однотактовой процедуре, определяемой выражением
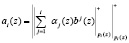 , (16)
, (16)
где i = 1, 2, .., n – количество оснований кода ПСКВ.
Результаты исследования и их обсуждение
Рассмотрим реализацию разработанного метода при минимальной избыточности кода ПСКВ. В системе ПСКВ с рабочими основаниями 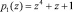 ,
, 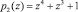 и контрольным основанием –
и контрольным основанием – 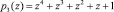 вычислим значение рабочего диапазона
вычислим значение рабочего диапазона
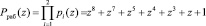 .
.
Определим значение ортогональных базисов и представим их в ОПС.
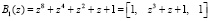 ;
;
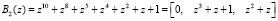 ;
;
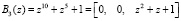 .
.
Переведем в ОПС код ПСКВ 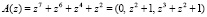 . Умножим остатки на ортогональные базисы, представленные в ОПС помодульно, учитывая количество превышения модуля. Результаты показаны в табл. 1.
. Умножим остатки на ортогональные базисы, представленные в ОПС помодульно, учитывая количество превышения модуля. Результаты показаны в табл. 1.
Таблица 1
Вычисление коэффициентов ОПС
|
Модули |
p1(z) = z4 + z + 1 |
p2(z) = z4 + z3 + 1 |
p3(z) = z4 + z3 + z2 + z+1 |
|
|
Код ПСКВ |
Произведение |
Произведение |
Превышение р2(х) |
Результат |
|
a1(z) = 0 |
0 |
0 |
0 |
0 |
|
a2(z) = z2 + 1 |
0 |
z3 + z2 |
z + 1 |
1 + (z + 1) = z |
|
a3(z) = z3 + z2 + 1 |
0 |
0 |
0 |
z |
|
ОПС |
v1(z) = 0 |
v2(z) = z3 + z2 |
– |
v3(z) = 0 |
Так как старший коэффициент v3 = 0, то код ПСКВ не содержит ошибку.
Пусть произошла ошибка по первому основанию. Тогда код ПСКВ 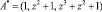 . Вычислим коэффициенты ОПС. Результаты вычисления коэффициентов ОПС показаны в табл. 2.
. Вычислим коэффициенты ОПС. Результаты вычисления коэффициентов ОПС показаны в табл. 2.
Таблица 2
Вычисление коэффициентов ОПС при наличии ошибки
|
Модули |
p1(z) = z4 + z + 1 |
p2(z) = z4 + z3 + 1 |
p3(z) = z4 + z3 + z2 + z + 1 |
|
|
Код ПСКВ |
Произведение |
Произведение |
Превышение р2(х) |
Результат |
|
a1(z) = 0 |
1 |
0 |
0 |
0 |
|
a2(z) = z2 + 1 |
0 |
z3 + z2 |
z + 1 |
1 + (z + 1) = z |
|
a3(z) = z3 + z2 + 1 |
0 |
0 |
0 |
z |
|
ОПС |
v1(z) = 1 |
v2(z) = z2 + z + 1 |
– |
v3(z) = 1 |
Таблица 3
Зависимость коэффициентов ОПС от ошибки для поля GF(24)
|
Величина ошибки |
Коэффициенты ОПС |
|
|
a4(z) |
a5(z) |
|
|
Δα1 = 1 |
z3 |
z3 + z2 + z |
|
Δα2 = 1 |
z3 + z + 1 |
z3 + z2 |
|
Δα2 = z |
z3 + z2 + z |
z3 + z |
|
Δα3 = 1 |
z2 + 1 |
z3 + z2 + z |
|
Δα3 = z |
z3 + z |
z3 + z2 + z + 1 |
|
Δα3 = z2 |
z3 + z2 |
z3 + z2 |
|
Δα3 = z3 |
1 |
z3 + z |
|
Δα4 = 1 |
z2 + z |
z3 + z2 + z |
|
Δα4 = z |
z3 + z2 |
z3 + z2 + z + 1 |
|
Δα4 = z2 |
1 |
z3 + z2 |
|
Δα4 = z3 |
z |
z3 + z + 1 |
|
Δα5 = 1 |
0 |
z |
|
Δα5 = z |
0 |
z2 |
|
Δα5 = z2 |
0 |
z3 |
|
Δα5 = z3 |
0 |
z + 1 |
Так как старший коэффициент v3 = 1, то код ПСКВ содержит ошибку.
Если в состав ПСКВ ввести два контрольных основания, удовлетворяющих условию (7), то непозиционный модулярный код сможет корректировать ошибки. В табл. 3 приведены значения старших коэффициентов ОПС для системы ПСКВ, имеющей:
– рабочие основания 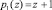 ,
, 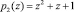 ;
; 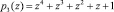 ;
;
– контрольные основания
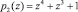 и
и 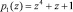 .
.
При этом значение 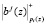 заранее учитывает количество превышение модуля pi(z) как перенос единицы при суммировании результата.
заранее учитывает количество превышение модуля pi(z) как перенос единицы при суммировании результата.
Для исследования процессов поиска и локализации ошибки в непозиционном коде полиномиальной системы классов вычетов полей GF(23), GF(24), GF(25) с использованием коэффициентов ОПС были разработаны математические модели. Проведенные исследования показали, что использование многоверсионной избыточности в методы вычисления коэффициентов ОПС для коррекции ошибок, позволяет сократить схемные затраты в 1,19 раз при обработке 16-разрядных данных по сравнению с методов маскирования отказов «2 из 3». При чем, с увеличением разрядности увеличивается эффективность схемной реализации.
Заключение
В статье проведена разработка нового метода использования многоверсионной избыточности модулярных кодов для коррекции ошибок на основе вычисления старших коэффициентов ОПС. Представлены результаты применения данного метода в кодах ПСКВ с одним и двумя контрольными основаниями. Показано, что использование минимальной избыточности позволяет обнаруживать факт ошибки. Проведенные исследования показали, что при использовании двух контрольных оснований код ПСКВ исправляет 100 % однократных ошибок, требуя при этом при обработке 16-разрядных данных в 1,19 раз меньше схемных затрата чем метод маскирования отказов «2 из 3».
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 16-37-50032.
Библиографическая ссылка
Белов С.П., Саркисов А.Б., Абакумова А.М., Калмыков И.А., Ряднов С.А. РАЗРАБОТКА МЕТОДА КОРРЕКЦИИ ОШИБКИ НА ОСНОВЕ ИСПОЛЬЗОВАНИЯ МНОГОВЕРСИОННОЙ ИЗБЫТОЧНОСТИ МОДУЛЯРНЫХ КОДОВ // Международный журнал прикладных и фундаментальных исследований. 2016. № 11-2. С. 198-202;URL: https://applied-research.ru/ru/article/view?id=10464 (дата обращения: 03.03.2026).

