Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сапогин В.Г. 1 Прокопенко Н.Н. 1 Панич А.Е. 2

---

1 Донской государственный технический университет

2 Институт высоких технологий и пьезотехники Южного Федерального университета

Предложен метод расчёта индуктивности сплошного немагнитного проводящего цилиндра произвольных геометрических размеров с азимутальной плотностью вихревого тока при наличии омических потерь и магнитных свойств токов Фуко. Получены радиальные распределения азимутальной компоненты вектора напряженности вихревого электрического поля, плотности токов Фуко, удельной тепловой мощности, выделяемой в локальной области проводящего цилиндра. Из энергетических соображений получена формула для динамической частотно-зависимой индуктивности сплошного цилиндра. Из неё следует, что динамическая индуктивность обращается в нуль для двух характеристических частот системы и имеет положительные и отрицательные значения. Предложен метод расчёта частотно-независимой токовихревой индуктивности тонкой проводящей цилиндрической плёнки. Исследуется наноразмерный эффект, возникающий в планарной индуктивности с перспективной технологией «проводящая плёнка внутри токового кольца». Обсуждаются свойства токовихревых индуктивностей с различными геометриями индуктора.

Статья в формате PDF

5006 KB

вихревое электрическое поле

динамическая индуктивность

положительная токовихревая индуктивность

отрицательная токовихревая индуктивность

перспективная технология «проводящая пленка внутри токового кольца» (ППВТК-технология)

1. Савельев И.В. Курс общей физики. Т. 2. – М.: Наука, Главная редакция физико-математической литературы. – 1988. – C. 496.

2. Сапогин В.Г., Прокопенко Н.Н., Манжула В.Г., Сапунцов Н.Е., Нестюрина Е.Е. Индуктивность сплошного проводящего цилиндра с азимутальной плотностью вихревого тока в низкочастотной области // Фундаментальные исследования. – 2013. – № 11 (часть 3). – С. 441-446.

3. Сапогин В.Г., Прокопенко Н.Н., Марчук В.И., Манжула В.Г., Будяков А.С. Индуктивные свойства микроскопического проводящего кольца с плотностью вихревого тока азимутального направления // Нано- и микросистемная техника. – 2014. – № 1. – С. 22-26.

4. Сапогин В.Г., Прокопенко Н.Н., Сапунцов Н.Е. Индуктивность цилиндрической плёнки с азимутальной плотностью вихревого тока // Материалы международной конференции «Актуальные проблемы электронного приборостроения». Т. II. Саратов, Россия, 25-26 сентября 2014 г. – С. 358-365.

5. Сапогин В.Г., Прокопенко Н.Н. О методах расчёта микроскопической интегральной индуктивности с высокой симметрией // Радиотехника. – 2015. – № 2. – 116-125.

6. Сапогин В.Г., Крутчинский С.Г., Прокопенко Н.Н., и др. Интегральные индуктивности и трансформаторы аналоговых микросхем СВЧ – диапазона. – Шахты: ГОУ ВПО «ЮРГУЭС», – 2010. – С. 273.

7. Vladimir G. Sapogin, Nikolay N. Prokopenko and Ludmila K. Sapogina. Solution of Solitary Current Inductor’s «Cutoff Frequency Problem» for EHF Applications. The International IEEE Conference on Microwawes, Communications, Antennas and Electronic Systems (COMCAS-2015). David Intercontinental Hotel 2-4 november 2015 Tel Aviv, Israel. 978-1-4799-7473-3/15/$31.00 ©2015 IEEE. 107774.pdf.

8. Ragonese Е., Biondi Т., Scuderi А., Palmisano G.A Lumped Scalable Physics-Based Model for Silicon Spiral Inductors. 0-7803-7530-0/02$17.00 ©2002 IEEE. P. 119-124.

9. Yue C.P. and Wong S.S. On-Chip Spiral Inductors with Paterned Ground Shields for Si-Based RFIC’s. IEEE J.Solid State Circuit, vol. 33, no. 5, p.p. 743-752, may 1999.

10. Widjaja A. and Sarangan A. Method for Fabrication Thin Film Structures with Negative Inductance. Case #: UD-488. US-Patent Pending; Publication # 20090261936. Inventor: Agus-Widjaja, et. al.

В мае 1999 года Yue и Wong опубликовали работу [9], в которой предложили принципиально новое технологическое решение для построения разнообразных планарных индуктивностей. Они исследовали три варианта планарного размещения спирального индуктора, кремниевой подложки и экрана (сплошного, либо узорчатого). В первом варианте планарный прямоугольный спиральный индуктор был помещён на поверхность кремниевой платформы без металлического экрана и назвали его NGS (No Ground Shield).

Во втором варианте добавлен сплошной экран. Конструкция была названа SGS (Solid Ground Shield). В третьем варианте сплошной экран был заменён на узорчатый экран. Такая конструкция была названа индуктор PGS (Patterned Ground Shield). Две технологические конструкции (NGS и PGS) обнаружили частотные свойства добротности, которые принципиально отличались от частотных свойств одиночных индукторов. Они давали растущие частотные зависимости добротности, которые достигали максимума на частоте около 2-х гигагерц и затем спадали к нулю на частотах около 7-8 Ггц. Как известно, нуль добротности индуктивности соответствует нулю индуктивности. Никаких количественных объяснений свойств нового класса индуктивностей предложено не было.

Итальянскими исследователями в 2002 году в работе [8] была создана планарная индуктивность, которая отличалась от индуктивности, исследованной в [9], цилиндрической геометрией. В ней цилиндрическая спираль была нагружена на слоистую цилиндрическую структуру, состоящую из модифицированных слоёв кремния, лежащего на проводящей медной подложке. Узор экрана имел радиальную структуру.

Эксперименты не только подтвердили ход частотных зависимостей добротности, найденные в [9], но и обнаружили, что на гигагерцах индуктивность RPGS – индуктора (Radial Patterned Ground Shield) может обратиться в нуль, а на более высоких частотах даже стать отрицательной. В [8] была предложена базовая физическая модель такой индуктивности, которая была выполнена в виде схемы на сосредоточенных параметрах. Она давала достаточно точные совпадения теории с проводимыми экспериментами.

В 2009 году исследователи из штата Огайо снова натолкнулись на тот факт, что многослойная интегральная индуктивность может стать отрицательной [10]. Проведённые с различным количеством двойных слоёв (один двойной слой из Al и Cu имел толщину 200 нм) эксперименты показали, при количестве слоёв, начиная с шести, частотная зависимость индуктивности содержит участки, на которых индуктивность принимает отрицательные значения.

Эксперименты в [10] также обнаружили, что индуктивность системы, состоящей из двух двойных слоёв, может быть положительной и практически частотно-независимой. Но, к сожалению, никаких физических моделей, которые объясняли бы полученные в своей работе результаты, предложено не было.

Все перечисленные индукторы устроены примерно одинаково. Вид частотных характеристик рассмотренных индукторов можно объяснить тем, что силовые линии магнитного поля индуктора были нагружены на проводящую или полупроводящую плёнку, которая прилегала к спиральному индуктору. Ток индуктора создавал своё переменное магнитное поле и магнитное поле отклика, формируемое токами Фуко, в проводящей плёнке. Взаимодействие тока индуктора с суммарным магнитным полем и приводило к появлению таких частотных характеристик, что его индуктивность на определённых частотах была положительной, а на других – отрицательной.

Как теперь становится понятным, причины этого связаны с магнитными эффектами, которые возникают при генерации вихревых токов Фуко и их взаимодействии с результирующим переменным магнитным полем, возникающим в цилиндрической проводящей плёнке. Цель предлагаемой работы объяснить не только существование частотно-зависимой токовихревой индуктивности, которая на определённых частотах может быть отрицательной, но и указать на возможность существования частотно-независимой положительной индуктивности.

Частотно-зависимая токовихревая индуктивность

Предположим, что сплошной проводящий немагнитный цилиндр находится во внешнем однородном переменном магнитном поле, направленном по оси z, 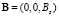. Его зависимость во времени имеет вид

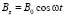, (1)

где B0 = const не зависит от цилиндрических координат системы и ограничено в радиальном направлении внешним радиусом цилиндра R, а в аксиальном направлении произвольной высотой цилиндра, обозначенной через h (см. рис. 1). Заметим, что цилиндр, как геометрическое тело, переходит в плёнку при условии h < R, а в тонкую цилиндрическую плёнку при условии h << R.

При такой ориентации переменное магнитное поле может порождать в цилиндре вихревое электрическое поле, напряженность которого 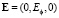имеет одну компоненту. Впервые экспериментальное доказательство существования такой возможной ориентации вихревого электрического поля было обнаружено при создании бетатронов – индукционных ускорителей электронов. В них как раз ускорение электронов и осуществляется вихревым электрическим полем, силовые линии которого представляют собой концентрические окружности. Они формируются электромагнитом специальной формы (см., например [1]). Вторая возможная ориентация вихревого электрического поля, напряженность которого имеет две компоненты 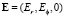, не реализуется.

Компоненты полей связаны между собой первым уравнением Максвелла, записанным в проекциях

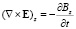. (2)

Полагая в (2), что фаза вихревого электрического поля совпадает по фазе со скоростью изменения магнитного поля

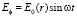, (3)

из уравнения (3) получим уравнение, связывающее E0(r) и B0

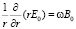. (4)

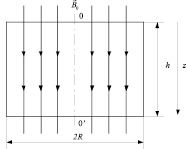
Рис. 1. Ориентация силовых линий магнитного поля B0 в пространстве цилиндра

Его решение для E0(r) имеет вид

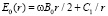. (5)

В решении (5) избавимся от особенности при 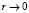, полагая C1 = 0. Это условие приводит к тому, что при B0 = 0 E0 = 0. Из (2) видно, что азимутальная компонента вектора напряженности вихревого электрического поля – линейная функция радиуса r с масштабом

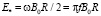. (6)

В масштабе напряжённости учтено соотношение 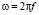. Тогда (5) с учётом (6) имеет вид

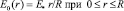. (7)

Электрическое поле в проводящем цилиндре создает вихревые токи Фуко, плотность тока которых имеет такое же направление в пространстве 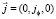. Плотность токов Фуко рассчитывается из дифференциального закона Ома

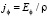, (8)

где ρ – удельное электрическое сопротивление проводящего цилиндра.

Из (8) видно, что плотность тока Фуко в однородной проводящей среде ρ = const также является линейной функцией радиуса и также зависит от времени, как и Eφ

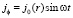, (9)

где j₀(r) связано с масштабом плотности тока

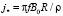(10)

соотношением

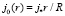. (11)

Из соотношения (10) видно, что при прочих равных условиях масштаб тока может достигать больших значений на высоких частотах для проводящей среды с малым значением удельного сопротивления r.

Удельная тепловая мощность, выделяемая в локальной области проводника при протекании токов Фуко, рассчитывается из закона Джоуля Ленца:

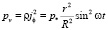, (12)

где

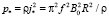(13)

масштаб объемной плотности тепловой мощности.

Как видно из (13), удельная мощность уже пропорциональна квадрату частоты и для проводящей среды с произвольным значением удельного сопротивления оказывается наиболее значительным на внешней границе цилиндра. Это может приводить к перегреву его внешней боковой поверхности на высокой частоте.

Тепловая мощность, выделяемая во всём цилиндре, находится из (12)

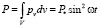, (14)

где масштаб тепловой мощности имеет вид

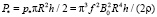. (15)

Вихревой ток, индуцированный во всём цилиндре, может быть получен из интегрирования плотности тока

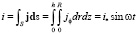, (16)

где

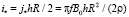(17)

масштаб индукционного тока.

Вихревая плотность токов Фуко (9) создаёт в пространстве цилиндра собственное магнитное поле B1. Это магнитное поле отклика вещества для исходной ориентации вихревых токов в цилиндрической системе координат имеет две проекции B1r и B1z. Направление проекции B1z для некоторых моментов времени во всех точках цилиндра противоположно внешнему магнитному полю В0. Предполагая, что компонента B1r не зависит от координаты z, распределение магнитного поля отклика вещества можно рассчитать из второго уравнения Максвелла, записанного в проекциях (частная производная компоненты B1r по переменной z опущена):

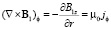. (18)

Интегрируя (18) для начального условия B1z(0) = 0, получим

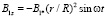, (19)

где

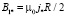(20)

масштаб индукции магнитного поля отклика вещества. Его можно связать с индукцией внешнего магнитного поля безразмерным параметром b

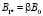, (21)

который указывает на различное влияние магнетизма токов Фуко

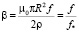, (22)

где

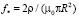(23)

масштаб частоты системы.

Средняя за период Т изменения поля магнитная энергия, поступающая в цилиндр, находится из интегрирования

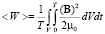, (24)

где результирующая индукция магнитного поля системы

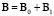. (25)

Тогда <W> состоит из двух слагаемых: средней за период энергии внешнего поля

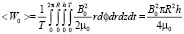. (26)

и средней энергии магнитного поля отклика вещества

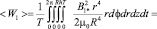
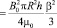. (27)

Интегрирование за период скалярного произведения 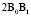обращается в нуль из-за наличия фазового сдвига π/2 между индукциями B1 и B0. В связи с этим между переменными полями B1 и B0 возникает своеобразная интерференция, которая и суммирует обе энергии

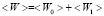. (28)

Вносимая за период магнитная энергия (28) расходуется на нагрев проводящего цилиндра Wq и ту часть энергии, которая запасается в индуктивность системы

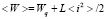. (29)

Тепловая энергия, расходуемая на нагрев цилиндра за период, вычисляется интегрированием (14) по времени

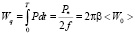. (30)

Среднее за период значение квадрата тока найдём из (16)

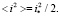(31)

Подставляя в (28) и (29) вычисленные энергии, получим частотную зависимость для приведённой токовихревой индуктивности цилиндра из энергетических соотношений

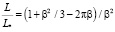, (32)

где

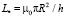(33)

масштаб индуктивности, который зависит только от геометрических размеров цилиндра. Он может принимать большие значения для тонких плёнок при выполнении условия h/R << 1.

Как видно из (32), индуктивность проводящего цилиндра обращается в нуль на двух характеристических частотах F1 и F2 (F1 < F2) и имеет низкочастотную неустранимую особенность при :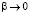

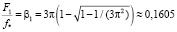. (34)

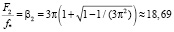. (35)

Нули индуктивности делят весь частотный интервал на три части. В низкочастотном интервале выполнено условие 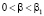. В нём индуктивность цилиндра положительная величина, убывающая с ростом частоты (проявляется слабый ферромагнетизм токов Фуко). Среднечастотный диапазон (выполнено условие 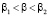), в котором индуктивность принимает отрицательные значения (проявляется сильный диамагнетизм токов Фуко). В этом интервале минимальное значение индуктивности 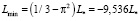достигается на частоте 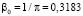. Высокочастотный диапазон (выполнено условие 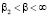), в котором она принимает положительные значения (снова проявляется слабый ферромагнетизм токов Фуко). На КВЧ её значения перестают зависеть от частоты и стремятся к значению 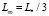. Что указывает на отличительное свойство динамической индуктивности – отсутствие частоты среза. Последнее утверждение требует экспериментальной проверки на КВЧ.

Эксперименты, проведённые с многослойными плёнками (число двойных слоёв больше 2) в [10], указывают на хорошее качественное совпадение теоретической частотной зависимости отрицательной индуктивности в среднечастотном диапазоне с экспериментом. На шести двойных слоях наблюдают две характеристические частоты (два нуля индуктивности), находящиеся несимметрично по обе стороны от её минимального значения. На десяти двойных слоях наблюдают только верхнюю характеристическую частоту. На тридцати двойных слоях в выбранный для экспериментов частотный диапазон ни один нуль индуктивности не попал.

Одним из существенных недостатков предлагаемой физико-математической модели динамической индуктивности является тот факт, что на сверхнизких частотах, по сравнению с масштабом частоты, частотная зависимость индуктивности имеет неустранимую особенность. Физические причины этого заключаются в том, что индуцированный за счёт электромагнитной индукции квадрат токов Фуко оказывается пропорционален квадрату частоты.

Поскольку динамическая индуктивность есть коэффициент пропорциональности между энергией магнитного поля и квадратом тока, то поэтому в конечное соотношение для индуктивности входит квадрат частоты в знаменателе. Когда квадрат частоты тока идёт в нуль, то потери на нагрев в системе становятся малыми, магнитное поле отклика становится слабым за счёт малости β, а энергия внешнего магнитного поля, закачиваемого в систему, остаётся постоянной величиной, совпадающей с энергией магнитного поля, запасённого в индуктивности. Из-за этого стремление тока к нулю даёт увеличение индуктивности, которое описывается особенностью, обратно пропорциональной квадрату частоты.

Существование особенности индуктивности приводит к тому, что динамическая индуктивность не переходит в статическую индуктивность на низких частотах. В экспериментах же, проведённых в [8], такой переход наблюдается всегда. Наличие особенности индуктивности на сверхнизких частотах указывает на достоинство предлагаемого метода. Он может быть применён для расчёта микроскопических индуктивностей в интервале высоких, сверхвысоких и крайне высоких частот, который начинается с частоты порядка 100 МГц.

Экспериментальные исследования поведения модели на сверхнизких частотах реальных индуктивностей цилиндрической пленки позволит ввести ограничения на значения нижней частоты среза, существующей в модели, ниже которой теория будет сильно расходиться с экспериментом.

Заметим, что в соотношении (29) не учтена магнитная энергия, которая поставляется в систему радиальной компонентой магнитного поля отклика вещества B1r. Если эту энергию учесть, то приведённая индуктивность цилиндра, начинает зависеть от относительного энергетического вклада радиальной компоненты как от параметра a.

В связи с чем (32) видоизменяется и имеет вид

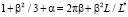, (36)

где второй независимый параметр системы a

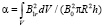, (37)

относительный положительный вклад радиальной компоненты в индуктивность сплошного проводящего цилиндра.

Как видно из (36), этот вклад не устраняет низкочастотную особенность, но приводит к изменению положения характеристических частот F1 и F2 индуктивности сплошного цилиндра. Положение первого корня зависит от параметра a по закону

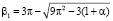, (38)

а положение второго корня

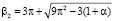. (39)

Нуль дискриминанта уравнения (36) указывает на то, что при равенстве

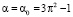(40)

корни частотной зависимости равны друг другу, а индуктивность проводящего цилиндра в этой точке обращается в нуль.

Это приводит к тому, что при небольшом относительном вкладе радиальной компоненты в магнитную энергию цилиндра (параметр a изменяется в области 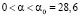) есть интервал частот, на котором индуктивность будет принимать отрицательные значения. При выполнении неравенства 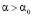(вклад радиальной компоненты в магнитную энергию цилиндра велик) у частотной зависимости индуктивности нулей нет и индуктивность цилиндра положительна для любых частот. В этом случае токи Фуко проявляют только слабые ферромагнитные свойства.

В табл. 1 даны 6 точек зависимости приведённых характеристических частот индуктивности (38) и (39) от параметра a.

Таблица 1

Расположение нулей частотной зависимости индуктивности от параметра α

Из табл. 1 видно, что с ростом a корни частотной зависимости приближаются друг к другу. Это уменьшает ширину среднечастотного интервала, в котором токи Фуко проявляют свои сильные диамагнитные свойства. Как показывают сравнения вычислений с известными экспериментами, параметр a для сплошной цилиндрической плёнки близок к нулю. Его действие следует учитывать в цилиндрических плёнках с геометрией кольца, имеющего конечную радиальную толщину.

Частотно-независимая токовихревая индуктивность

Как показывают эксперименты, проведённые в [10], помимо динамической индуктивности, рассмотренной ранее, возможно ещё одно состояние токовихревой индуктивности. Она может быть частотно-независимой в определённом диапазоне частот и принимать положительные значения. В этих состояниях снова проявляются слабые ферромагнитные свойства токов Фуко.

Предположим, что сплошная проводящая немагнитная цилиндрическая плёнка находится, как и ранее, во внешнем однородном переменном магнитном поле, направленном по оси z, и имеет только одну компоненту 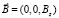. Это внешнее для плёнки магнитное поле имеет ту же зависимость от времени, что и ранее

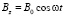. (41)

Для простоты предполагаем, что однородное в пространстве магнитное поле B0 = const не зависит от цилиндрических координат системы и ограничено в радиальном направлении внешним радиусом цилиндра R, а в аксиальном направлении произвольной высотой цилиндра, обозначенной через h.

На рис. 2 указаны направления векторов и силовых линий внешнего переменного магнитного поля относительно оси плёнки. Показаны направления азимутальной компоненты вектора плотности тока Фуко, имеющей единственную компоненту jj, для некоторого момента времени.

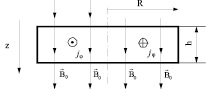
Рис. 2. Направление в пространстве основных векторов задачи

При такой ориентации переменное магнитное поле будет порождать в цилиндрической плёнке вихревое электрическое поле, напряженность которого 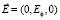имеет только одну компоненту, как и ранее. Компоненты полей связаны между собой первым уравнением Максвелла, записанным в цилиндрической системе координат (r, φ, z)

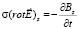, (42)

где 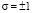– уточняющий знаковый множитель. Уравнение (42) отличается от (2). Это отличие включает в себя две возможные ориентации ротора вихревого электрического поля по отношению к исходному направлению вектора B0. Как показывают эксперименты, проведённые в [10], значение 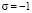возникает в плёнках с толщиной десятки и сотни нанометров. В таких сверхтонких плёнках токи Фуко формируют частотно-независимую положительную индуктивность, проявляя свои слабые ферромагнитные свойства. Этот эффект проявляет себя только в проводящих плёнках с толщиной от 10 до 500 нм.

Значение 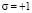реализуется при протекании токов Фуко в проводящих цилиндрах в макроскопических масштабах, когда проявляются их сильные диамагнитные свойства. Высоты проводящих цилиндров при этом должны быть больше радиуса и значительно больше 1 мкм. Такие значения величин преобразуют плёнку в цилиндр, токи Фуко которого обычно диамагнитны для определённых распределений в пространстве магнитных полей индуктора.

Полагая в (42), что

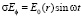, (43)

из уравнения (43) получим уравнение, связывающее E0(r) и B0

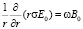. (44)

Его решение для E0(r) имеет вид

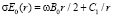. (45)

В решении (45) избавимся от особенности при 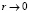, полагая произвольную постоянную C1 = 0. Это условие приводит к тому, что при B0 = 0 E0 = 0. Из (42) видно, что азимутальная компонента вектора напряженности вихревого электрического поля – линейная функция радиуса r с масштабом

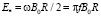. (46)

В масштабе напряжённости учтено соотношение 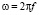. Тогда (45) с учётом (46) имеет вид

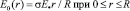. (47)

Электрическое поле в проводящем цилиндре создает вихревые токи Фуко, плотность тока которых имеет такое же направление в пространстве 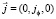. Плотность токов Фуко рассчитывается из дифференциального закона Ома

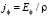, (48)

где ρ – удельное электрическое сопротивление проводящей плёнки.

Из (48) видно, что плотность тока Фуко в однородной проводящей среде r = const также является линейной функцией радиуса и также зависит от времени, как и Eφ

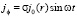, (49)

где j₀(r) связано с масштабом плотности тока

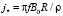(50)

соотношением

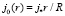. (51)

Вихревой ток, индуцированный во всей плёнке, может быть получен из интегрирования плотности тока в цилиндрических координатах

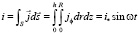, (52)

где

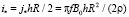(53)

масштаб индукционного тока.

Амплитуда электродвижущей силы, возникающей в пространстве цилиндра (плёнки) для фиксированного значения s, зависит квадратично от локального значения радиуса r

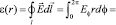
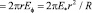. (54)

А средняя по радиусу амплитуда электродвижущей силы имеет вид

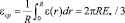. (55)

Среднее омическое сопротивление проводящей плёнки переменному вихревому току не зависит от времени

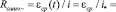
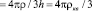. (56)

Этим сопротивлением обладает цилиндр (плёнка) на любой частоте и при любых значениях переменного тока (для линейного режима протекания). С точностью до постоянной величины оно совпадает с омическим сопротивлением квадрата.

Плотность вихревых токов Фуко (49) создаёт в пространстве цилиндра собственное магнитное поле 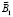. Это магнитное поле отклика вещества на внешнее воздействие для исходной ориентации вихревых токов в цилиндрической системе координат имеет одну проекцию B1z. Направление проекции B1z во всех точках цилиндра противоположно внешнему магнитному полю В0. В этом и заключается основная причина диамагнетизма, проявляемого токами Фуко. Но как показано ниже, исключительно важную роль играют ещё и фазовые соотношения между взаимодействующими полями.

Распределение магнитного поля отклика вещества можно рассчитать из второго уравнения Максвелла, записанного в проекциях:

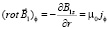. (57)

Интегрируя (57) для граничного условия 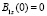с учётом (49), получим

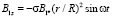, (58)

где

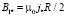(59)

масштаб индукции магнитного поля отклика вещества. Так же как и ранее его можно связать с индукцией внешнего магнитного поля безразмерным параметром b

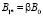, (60)

который указывает на влияние магнетизма токов Фуко

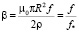, (61)

где

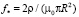(62)

масштаб частоты системы. Как видно из (62), масштаб частоты системы не зависит от толщины цилиндрической плёнки.

Исследуем индуктивные свойства токовихревой плёнки, усреднённые по времени. Найдём её потоковую индуктивность из соотношения

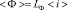, (63)

где под <Ф> будем понимать суммарный средний за полупериод поток, пересекающий проводящую плёнку, который формируется внешним переменным магнитным полем B0 и магнитным полем отклика вещества B1. Под значением <i> будем понимать среднее значение переменного тока одного направления за полупериод. Тогда коэффициент пропорциональности между ними LФ будет играть роль средней потоковой индуктивности.

Поток внешнего переменного однородного магнитного поля имеет вид

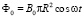, (64)

а поток переменного неоднородного магнитного поля отклика вещества вычисляется из соотношения

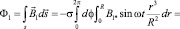
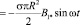. (65)

Из (65) видна важная роль множителя s, который может принимать два различных значения.

Среднее значение суммарного потока за полупериод имеет вид

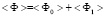, (66)

где

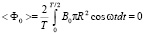, (67)

а

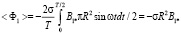. (68)

Из (67), (68) видно, что средний поток внешнего поля за полупериод всегда обращается в нуль, а среднее значение потока поля отклика может быть как положительным, так и отрицательным.

Подставляя (67) и (68) в (66) с учётом связи (63), получим

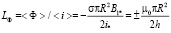. (69)

Из (69) следует, что средняя за полупериод индуктивность планарного токового слоя зависит только от геометрических размеров плёнки, но не зависит от частоты и может быть как положительной, так и отрицательной величиной. Её значение в 2 раза меньше, чем масштаб динамической индуктивности (33) и определяется только геометрическими размерами плёнки.

Добротность потоковой индуктивности плёнки не зависит от её толщины, но имеет линейную зависимость от рабочей частоты

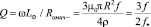. (70)

Из (70) видно, что добротность Q > 1 будет у цилиндрических плёнок, рабочая частота которых больше, чем .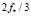

Как показывают эксперименты [10], величины R и h – могут совпадать с геометрическими размерами одиночного элементарного токового вихря, который возбуждается в проводящей плёнке. При соотношении h < R толщина цилиндрической плёнки будет совпадать с толщиной одиночного элементарного токового вихря только для случая, когда толщина плёнки меньше 500 нм. При этих условиях реализуется положительная частотно-независимая потоковая индуктивность, а вихревые токи Фуко проявляют свои слабые ферромагнитные свойства.

Причина этого в том, что в этом случае реализуется значение s = –1. Вихревые токи Фуко создают магнитное поле отклика, которое в течение полупериода направлено по оси z и создаёт положительное значение для усреднённого потока. Направления полей B0 и B1 в этом случае на первой и второй четверти периода указаны на рис. 3. На рис. 3 ток i0 – ток, текущий в токовом кольце и создающий внешнее для плёнки поле B0.

На втором полупериоде величина потоковой индуктивности (69) остаётся прежней по причине того, что поток индукционного поля B1 и вихревой ток изменяют свои значения на противоположные.

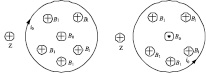
Рис. 3 – Направления полей B0 и B1 при dB₀ / dt < 0, σ = – 1 для двух ориентаций вектора B0 для первой и второй четверти периода (слабые ферромагнитные свойства токов Фуко)

Если h > 1 мкм и условие h < R не выполнено (возникает проводящий цилиндр), то возможны случаи, когда проводящий цилиндр находится, либо в состоянии отрицательной частотно-независимой индуктивности (токи Фуко проявляют свои сильные диамагнитные свойства в макроскопических масштабах), либо в состоянии частотно-зависимой динамической индуктивности, которая обращается в нуль на двух характеристических частотах (см. предыдущий раздел).

Причины появления отрицательной частотно-независимой индуктивности в случае s = + 1 заключаются в том, что вихревые токи Фуко создают магнитное поле отклика, которое в течение полупериода направлено против оси z. Это создаёт отрицательное значение для усреднённого потока. Направления полей B0 и B1 в этом случае на первой и второй четверти периода указаны на рис. 4. На рис. 4 ток i0 – ток, текущий в токовом кольце и создающий внешнее для плёнки поле B0.

На втором полупериоде величина потоковой индуктивности (66) остаётся прежней по причине того, что поток индукционного поля B1 и вихревой ток изменяют свои значения на противоположные.

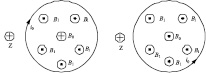
Рис. 4. Направления полей B0 и B1 при dB0 / dt < 0, σ = + 1 для двух ориентаций вектора B0 для первой и второй четверти периода (сильные диамагнитные свойства токов Фуко)

В современных чипах приемлемым значением интегральной индуктивности является значение 10 нГн. В табл. 2 приведены значения толщины плёнки в нанометрах и соответствующий радиус в микрометрах, который даёт фиксированное значение индуктивности плёнки в 10 нГн.

Таблица 2

Геометрические размеры плёнки для индуктивности 10 нГн

Расчёты для толщины плёнки больше 500 нм не приводятся по причине того, что одиночный элементарный токовый вихрь, который возбуждается в проводящей плёнке, в таком случае может оказаться нестабильным и перейти в другое частотно-зависимое состояние динамической индуктивности.

Частотный диапазон работы такой плёнки определяется из масштаба частоты (62). Он не зависит от толщины плёнки и лежит в пределах

0,1f* < f < 10f*. (71)

Табл. 2 указывает на возможность дальнейшего уменьшения площади, занимаемой интегральной индуктивностью. Такое уменьшение может привести к достижению предельных значений поверхностной плотности индуктивности вплоть до порядка 10 Гн/м2.

Наноразмерный эффект перспективной технологии «проводящая плёнка внутри токового кольца»

Планарные индуктивности, которые реализуются на диэлектрической подложке в виде многовитковых круглых, спиральных, квадратных или более сложных геометрических форм широко используются в современных устройствах связи и телекоммуникаций в структурах «система на кристалле» или «система в корпусе» [6].

В ряде случаев интегральная индуктивность, предназначенная для СВЧ диапазона, выполняется в виде одного витка [6] из напыляемой на подложку металлической пленки, образующей токовое кольцо. Однако такое конструктивно-технологическое решение уменьшает численное значение индуктивности до единиц наногенри (она изменяется в диапазоне от 0,5 до 3,5 нГн для геометрических размеров от 20 мкм до 100 мкм, [6]).

Рассмотрим конструкцию планарной индуктивности, которая использует обнаруженный выше наноразмерный эффект при своей реализации. Она приведена на рис. 5 и использует известную одновитковую топологию её создания [6].

Во внутреннюю область витка (токового кольца) из металлической пленки толщиной h1 введена дополнительная тонкая пленка толщиной h2 << h1 радиусом R < R1 из материала, обладающего заданной электропроводностью и не имеющего электрического контакта с витком.

На рис. 5 приняты следующие обозначения: R – радиус дополнительной тонкой плёнки, h2 – ее толщина; R1 – внутренний радиус витка (токового кольца) из металлической пленки толщиной h1; R2 – внешний радиус витка; 1 и 2 выводы интегральной индуктивности для ее включения в электронную схему.

Индуктивность конструкции L (рис. 5) относительно выводов 1 и 2 складывается из двух составляющих

L = Lк + Lф, (72)

где Lк – индуктивность витка (токового кольца), расчет которой можно выполнить на основе формул и графиков, представленных в [6]; Lф – потоковая индуктивность дополнительной тонкой цилиндрической пленки h2, рассчитывается по соотношению (69). В нём букву h следует заменить на h2.

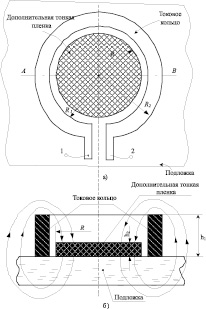
Рис. 5. Предлагаемая конструкция индуктивности (а) и ее разрез по вертикальному сечению АВ (б)

В табл. 3 приведены значения потоковой индуктивности Lф, рассчитанные из (69), которые можно реализовать для тонкой плёнки радиусом R = 50 мкм. Суммарная положительная индуктивность системы будет определяться из (72).

Таблица 3

Зависимость потоковой индуктивности Lф тонкой плёнки от ее толщины h2

При этом удельное сопротивление тонкой плёнки не влияет на величину индуктивности между выводами 1 и 2, а изменяет только частотный диапазон, в котором такая индуктивность будет оставаться частотно-независящей. Диапазон рабочих частот для проводящей пленки можно оценить из условия (71). Значения масштаба частоты, зависящего от удельного сопротивления тонкой плёнки, рассчитанные из соотношения (62), представлены в табл. 4.

Таблица 4

Масштаб частоты проводящей плёнки радиусом 50 мкм

Из табл. 3 и 4 видно, что использование, например, алюминия при напылении дополнительной тонкой плёнки радиусом R = 50 мкм и толщиной h2 = 100 нм позволит получить индуктивность тонкой плёнки Lф = 50 нГн. Такая плёнка будет обеспечивать частотно-независимую индуктивность в диапазоне частот от 0,5 до 50 МГц.

Применение плёнки тех же геометрических размеров из нихрома обеспечивает постоянство индуктивности в диапазоне от 20 МГц до 2 ГГц; из меди – от 0,3 до 30 МГц; из вольфрама – от 1 до 100 МГц; из никеля – от 1,2 до 120 МГц; из кремния – от 20 Ггц до 2 ТГц.

Предлагаемая нами конструкция положительной планарной индуктивности с технологией «проводящая плёнка в токовом кольце» имеет существенные преимущества по величине получаемой микроскопической интегральной индуктивности в сравнении с классическим одновитковым решением. Наноразмерный эффект, обнаруженный экспериментально в [10] и подтверждённый теоретически в этой работе, позволяет реализовать более высокие значения микроскопической индуктивности. Как видно из табл. 3, индуктивность изменяется в диапазоне от 100 нГн до 14 нГн, что значительно лучше (в 7-50 раз) максимальной индуктивности известных в КМОП – традиционных технологиях, достигаемых в одном слое.

Выбор значения удельного сопротивления материала, из которого создается тонкая пленка, позволяет «сдвигать» рабочий диапазон частот предлагаемой индуктивности в заданный частотный диапазон. Но, необходимо учитывать, что повышение рабочего диапазона частот будет приводить к увеличению омического сопротивления плёнки переменному току. Наиболее критичным этот эффект будет для сверхтонких плёнок.

Заключение

Эксперименты, выполненные с однослойными и многослойными проводящими плёнками, а также с проводящими цилиндрическими стержнями, указывают на следующие особенности получения положительной или отрицательной токовихревой индуктивности. Особую роль в них играет геометрия токового индуктора. По геометрии создаваемых силовых линий магнитного поля токовые индукторы следует классифицировать как открытые и закрытые.

К закрытым индукторам отнесём классические соленоиды конечной длины. В них средняя плотность силовых линий магнитного поля внутри всегда выше, чем снаружи. На изменение индуктивности соленоида и его частоты среза можно влиять различными способами. Наиболее существенные изменения можно получить, связывая магнитные силовые линии проводящими стержнями или плёнками с различным количеством слоёв. Плёнки устанавливаются поперек силовых линий во внутренней области соленоида.

Для тонкой плёнки, с наноскопической толщиной, положительная индуктивность соленоида может существенно возрасти. При этом должна возникнуть частотно-независимая индуктивность. Она может увеличить частоту среза. В толстой или многослойной плёнке возможно появление состояния динамической индуктивности. На разных частотах суммарная индуктивность системы может иметь положительные значения индуктивности, отличающиеся от исходной индуктивности соленоида.

Расположение соленоида на полупроводящей или проводящей подложке связывает только незначительную часть внешних силовых линий магнитного поля. Это будет слабо изменять результирующую индуктивность соленоида и его частоту среза.

Заполнение проводником всего пространства внутри соленоида даёт максимальный эффект отрицательной индуктивности, вносимой проводящим стержнем. При этом суммарная индуктивность системы соленоид-стержень всегда будет уменьшена, но останется положительной.

К открытым индукторам следует отнести индукторы, выполненные в виде планарной спирали. Такой индуктор создаёт магнитные силовые линии, которые симметрично расположены в обоих полупространствах. Расположение с одной стороны такого индуктора проводящей плёнки с наноскопической толщиной, увеличит суммарную положительную индуктивность системы. Она будет частотно-независимой. Расположение с разных сторон спирального индуктора двух одинаковых проводящих плёнок с наноскопической толщиной ещё больше увеличит положительную суммарную индуктивность системы с сохранением её частотных свойств.

Расположение с одной стороны спирали либо толстой проводящей, либо многослойной плёнки может дать состояние динамической индуктивности. В этом случае суммарная индуктивность системы станет отрицательной и будет зависеть от частоты. Расположение с обеих сторон спирали таких плёнок ещё больше увеличит отрицательную индуктивность системы. Увеличивая число слоёв, можно пропорционально их количеству повышать суммарную отрицательную индуктивность открытой системы.

Статья подготовлена по проекту № 8.374.2014/К Госзадания Минобрнауки РФ на 2014-2016 гг.

Библиографическая ссылка