Формулировка целей исследования:
Цель 1. Задача интерпретации: выявление функциональных зависимостей затрат на транспортное обслуживание и степень выполнения заявок на доставку от количества, используемых транспортных средств (собственных и заемных), дистанции перевозки и продолжительности простоев.
Цель 2. Задачи оптимизации:
a. Определить оптимальный состав собственных и заемных транспортных средств, позволяющих осуществить своевременное и ритмичное обслуживание строительного объекта.
b. Определить рациональность использования одного из двух альтернативных материалов – шлака или скалы с точки зрения транспортного обслуживания.
Целью направленного вычислительного эксперимента является выбор таких управляющих параметров, при которых стратегия управления предприятием будет оптимальной.
Функция отклика:
Y1 – затраты на транспортное обслуживание строительного объекта;
Y2 – средняя загруженность собственных автотранспортных средств;
Y3 – средняя загруженность автотранспортных средств сторонних организаций.
В моделируемой системе к основному показателю качества отнесем затраты на транспортное обслуживание строительного объекта, определяемых количеством используемых автомобилей, позволяющих добиться ритмичности и своевременности поставок (на конец каждого дня наряды должны быть выполнены полностью). Для расчета затрат будем суммировать стоимость расхода ГСМ собственными автотранспортными средствами и стоимость услуг по автотранспортному обслуживанию сторонних организаций.
Факторы:
X1 – количество используемых собственных автотранспортных средств;
X2 – количество используемых автотранспортных средств сторонних организаций
X3 – расстояние между альтернативными материалами (шлаком и скальной породой).
X1, Х2, X3 – изменяемые и управляемые факторы.
В модели также учитываются неуправляемые случайные факторы.
Выбор экспериментальной области факторного пространства связан с тщательным анализом априорной информации. Для этого определим уровни варьирования каждого фактора в табл. 1.
Таблица 1
Уровни варьирования управляемых факторов
|
X1 |
X2 |
Х3 |
|
|
Основной уровень |
2 |
4 |
- |
|
Интервал варьирования |
0 |
1 |
6 |
|
Верхний уровень |
2 |
5 |
30 |
|
Нижний уровень |
2 |
4 |
24 |
При таком анализе было определено, что собственных автотранспортных средств недостаточно для обслуживания строительного объекта, поэтому нижний уровень фактора X1 равен 2. Следовательно, первоначально считающийся изменяемый фактор будет в данном эксперименте постоянным [1, 2]. Для X2 нижний уровень варьирования 4, так как по предположениям именно с этого уровня транспортное обслуживание приобретает ритмичный и своевременный характер.
Выберем план с разрешающей способностью III – N = 23
Y = β0 + β1X1 + β2X2 + β3X3 +β12X1X2 +β23X2X3 +β13X1X3 +β123X1X2X3 +e
Так как постулируется линейная модель, то предполагается, что эффекты взаимодействия близки к нулю, и поэтому 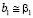 ,
, 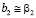 ,
, 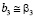 .
.
Матрица планирования эксперимента
|
X1 |
X2 |
X3 |
Y |
|
- |
- |
- |
Y1 |
|
- |
- |
+ |
Y2 |
|
- |
+ |
- |
Y3 |
|
- |
+ |
+ |
Y4 |
Определяющий контраст 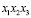 . Коэффициенты линейного уравнения будут оценками:
. Коэффициенты линейного уравнения будут оценками:
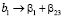 ,
, 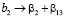 ,
, 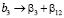 .
.
По каждому набору факторов проведено четыре прогона в системе Arena.
В результате были получены результаты, сведенные в табл. 2:
Таблица 2
Средние значения откликов
|
х1 |
х2 |
x3 |
Y1срi |
Y2срi |
Y3срi |
|
2 |
4 |
24 |
1081954 |
1,99 |
3,84 |
|
2 |
4 |
30 |
- |
- |
- |
|
2 |
5 |
24 |
1099470 |
1,99 |
3,94 |
|
2 |
5 |
30 |
1147056 |
1,96 |
4,13 |
В табл. 2 знак “-” означает, что в модели начинает расти очередь необслуженных заявок, о чем предупреждает система Arena и имитация заканчивается [3, 4]. Данная ситуация является следствием того, что увеличение расстояния сказывается на неспособности данного количества транспортных средств выполнить наряды своевременно,
Y1ср= 1109493 D1 = 1134918009 σ1 = =33688,54;
Y2ср= 1,97(6) D2 = 0,00023333 σ2 = =0,01527525;
Y3ср = 3.96(6) D3 = 0,022033 σ3 = =0,148436.
Обработка результатов эксперимента
Проверим постулаты регрессионного анализа для Y1:
1) Функция отклика – случайная величина, распределенная по нормальному закону со средним 1109493 и стандартным отклонением 33688,54, что подтверждено с помощью теста 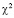 , который возвращает вероятность 0,507 для
, который возвращает вероятность 0,507 для 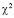 статистики.
статистики.
2) Однородность дисперсий
Отношение максимальной дисперсии к минимальной равно 589,37. Табличное значение F-критерия равно 33757,5 при степенях свободы f1=k=3 и f2=n–(k+1)=4. Расчетное значение меньше табличного, следовательно, принимается гипотеза об однородности дисперсий [5, 6].
3) Значение факторов Х1, Х2 и X3 – не случайные величины, так как установление фактора на некотором заданном уровне существенно точнее, чем точность определения отклика.
4) 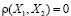 > корреляционная зависимость слаба, факторы не коррелированны.
> корреляционная зависимость слаба, факторы не коррелированны.
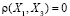 > корреляционная зависимость слаба, факторы не коррелированны.
> корреляционная зависимость слаба, факторы не коррелированны.
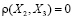 > корреляционная зависимость слаба, факторы не коррелированны.
> корреляционная зависимость слаба, факторы не коррелированны.
Расчеты проведены средствами Exсel.
Расчет коэффициентов регрессии
Применив метод наименьших квадратов (функция ЛИНЕЙН в Excel ) получим следующие коэффициенты:
b0 = 32551
b1 = 32551
b2 = 41309
b3 = 9390,6667
Y1ср = 32551x1+41309x2+ +9390,6667x3+32551.
Оценка адекватности математической модели
Вычислим значения Y1ср, рассчитанное по найденной функции (см. табл. 3).
Таблица 3
Расчетное и модельное значения откликов
|
X1 |
X2 |
X3 |
Y1ср по модели |
Y1ср расчетное |
|
2 |
4 |
24 |
1081954 |
1082047 |
|
2 |
4 |
30 |
– |
– |
|
2 |
5 |
24 |
1099470 |
1099554 |
|
2 |
5 |
30 |
1147056 |
1147055 |
Применим F-тест для сравнения совокупностей. F-тест = 0,996970715. Полученное значение меньше табличного (<6,39, при уровне значимости 0,05), что говорит об адекватности полученной модели. Поэтому с доверительной вероятностью 0,05 можно утверждать, что модель адекватна.
Интерпретация результатов
Т.к. коэффициенты регрессии указывают на силу влияния фактора на отклик можно сказать, что при увеличении значения любого из трех факторов значение функции увеличится. Величина коэффициента соответствует вкладу данного фактора в величину отклика при переходе фактора с 0-го уровня на верхний или на нижний. Эффект от фактора равен удвоенному коэффициенту регрессии, эффекты представлены в табл. 4 и расположены в порядке убывания силы из влияния на параметр оптимизации.
Таблица 4
Вклад факторов в величину отклика
|
Фактор |
Вклад в величину отклика |
|
Количество используемых собственных автотранспортных средств |
1059567601 |
|
Количество используемых автотранспортных средств сторонних организаций |
1706433481 |
|
Расстояние между альтернативными источниками материалов |
88184620,44 |
Полученные результаты совпадают с результатами анализа чувствительности: затраты на транспортное обслуживание строительства данного строительного объекта больше зависят от количества используемых собственных транспортных средств и средств сторонних организаций, чем от разницы в расстоянии между альтернативными источниками.
Оптимизация
В предыдущих пунктах доказано, что модель адекватно отражает результаты имитационного моделирования, следовательно, можно приступать к решению поставленной задачи оптимизации.
Решение первой задачи оптимизации заключалось в определении рациональности использования одного из двух альтернативных материалов – шлака или скалы с точки зрения транспортного обслуживания.
Исходя из табл. 4, с точки зрения транспортного обслуживания было установлено, что выгоднее осуществлять строительство с использованием скальной породы, чем с использование шлака. Решение второй задачи оптимизации заключалось в анализе очередей на выполнение нарядов, степени загрузки транспортных средств, а также затрат на них.
Согласно сгенерированным системой Arena отчетам были определены средние длины очередей заявок-нарядов, ожидающих транспортное средство.
Для X1=2, X2=4, X3=24 средняя длина очереди по некоторым из них больше 1, следовательно, часть заявок на конец дня не выполняются. Загруженность собственных автотранспортных средств равна 0,96, транспортных средств сторонних организаций 0,96. Средняя стоимость обслуживания равна 1081954 руб.
Для X1=2, X2=5, X3=24 средняя длина очереди по каждым типам нарядов равна меньше 1, что говорит о рациональности подобранного состава собственных транспортных средств и транспортных средств сторонних организаций, позволяющих осуществить своевременное и ритмичное обслуживание строительного объекта. Загруженность собственных автотранспортных средств равна 0,96, транспортных средств сторонних организаций 0,788. Загруженность транспортных средств сторонних организаций меньше чем в предыдущем варианте, поэтому разница в стоимости такого варианта обслуживания равна по сравнению с предыдущим составляет 17516 руб. Такая загруженность объясняется привлечением средств сторонних организаций только в пики нагрузок системы. Средняя стоимость обслуживания равна 1099470 руб.
Таким образом, предпочтительный вариант транспортного обслуживания с позиции обеих задач оптимизации, когда грузоперевозки материалов на строительный объект осуществляют 2 собственных самосвала, 5 самосвалов сторонних организаций, а также строительство ведется с использованием скальной породы.
Библиографическая ссылка
Новикова Т.Б., Курзаева Л.В. ОЦЕНКА АДЕКВАТНОСТИ ИМИТАЦИОННОЙ МОДЕЛИ ТРАНСПОРТНОГО ОБСЛУЖИВАНИЯ СТРОИТЕЛЬНЫХ ОБЪЕКТОВ // Международный журнал прикладных и фундаментальных исследований. 2016. № 12-2. С. 206-209;URL: https://applied-research.ru/ru/article/view?id=10807 (дата обращения: 03.03.2026).

