Межзеренные границы в поликристаллических металлах представляют собой поверхности раздела двух сопрягающихся кристаллитов. Различные технологии получения поликристаллических агрегатов приводят к геометрическим формам границ, в общем случае не являющимися плоскими. Такие границы обладают повышенной свободной энергией. Стремление системы к равновесию приводит к уменьшению этой энергии путем фрагментации границы, т.е. разбиению ее на энергетически выгодные плоские фрагменты. Несмотря на увеличение общей площади поверхности границы, ее энергия в целом понижается. Описанный процесс носит название фасетирования границы. Он является зернограничным фазовым переходом первого рода.
Условия неизменности среднего макроскопического положения границы, минимума ее поверхностной энергии, а также жёсткие условия сопряжения на ее краях требуют, чтобы различные фасетки стремились к определённым ориентациям, общее количество которых для данной границы обычно невелико (обычно две – четыре). Таким процессом сопровождается релаксация неравновесной структуры границ со всевозможными разориентациями соседних зёрен.
Целью настоящей работы является описание механизмов фазового перехода фасетирования межзеренной границы.
Механизм фасетирования границ
Если конечная форма границы представляется в виде цилиндрической поверхности с ломаной направляющей, то она является одномерно фасетированной (граница наклона). В случае двумерно фасетированой границы ее форма образована примыкающими друг к другу пирамидальными выступами с вершинами, направленными по обе стороны от нее (граница общего типа). В обоих случаях равновесная структура границы предполагает вполне определенные пространственные ориентации плоских сегментов-фасеток, количество которых равно двум или трем соответственно [1]. Если разориентация сопрягающихся вдоль границы зерен соответствует специальной, то фасетирование заключается в переходе от плоскости с низкой плотностью упаковки в решетке совпадающих узлов к сегментам, лежащим в плотноупакованных плоскостях.
Считаем, что ономерное фасетирование начинается с появления зародыша первого порядка в виде правильной пирамиды со стороной a квадрата в основании и углом между основанием и боковой гранью α [2]. Две боковые грани, параллельные образующей, имеют низкую удельную поверхностную энергию γ1, а поверхностная энергия двух других граней γ2 не является энергетически выгодной. Энергия образования такого зародыша равна
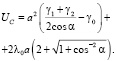 (1)
(1)
Здесь γ0 – удельная поверхностная энергия исходной границы, γ0 – удельная энергия линий сопряжения всех граней. Приравняв нулю производную (1) по a, можно определить критический размер зародыша и энергию его образования:
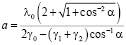 ;
;
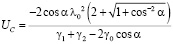 . (2)
. (2)
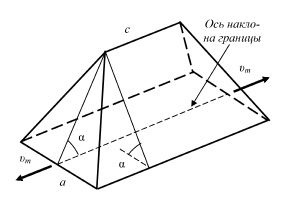
Рис. 1. Растущий зародыш первого порядка
Рост зародыша первого порядка происходит путем миграции в противоположные стороны вдоль образующей со скоростью υm боковых граней с энергией γ2, так что пирамида становится вальмовым многогранником (рис. 1).
Энергия растущего зародыша уменьшается по мере возрастания длины ребра c, сопрягающего энергетически выгодные фасетки. Выражая энергию такой конфигурации через геометрические параметры и вычисляя затем производную по c, находим движущую силу, действующую на перемещающиеся торцевые грани площади S:
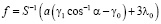 . (3)
. (3)
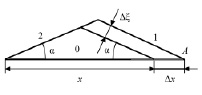
Рис. 2. Форма растущих фасеток: 0 – первоначальное положение границы; 1 и 2 – две ориентации фасеток; Δξ – смещение фасетки
Используя теорию гомогенного образования зародышей новой фазы, можно считать, что время образования критического зародыша первого порядка составляет величину
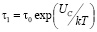 ,
,
где τ0 – период атомных колебаний, k – константа Больцмана, T – термодинамическая температура. Время его роста до формирования одномерного зародыша второго порядка зависит от размера зерна d и определяется выражением
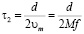 .
.
Здесь M – миграционная подвижность границы. Полное время появления зародыша фасетирования 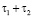 .
.
Дальнейший процесс осуществляется путем роста зародыша второго порядка. Сечение его плоскостью, нормальной к образующей, показано на рис. 2. Этот рост происходит за счет миграции боковых его граней 1 и 2. Отметим, что имеется некоторая аналогия кинетики рассматриваемого процесса фасетирования границы и кинетики кристаллизации расплава с учётом столкновения растущих кристаллов [3]. Согласно [4] доля фасетированной площади границы ψ(t) к моменту времени t после появления зародыша дается выражением
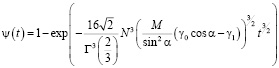 . (4)
. (4)
где Г(x) означает гамма-функцию. Общее количество фасеток на единице длины полностью фасетированной границы равно
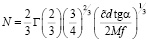 , (5)
, (5)
где 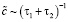 – скорость образования зародышей на единице длины нерелаксированной границы. Время процесса фасетирования составляет
– скорость образования зародышей на единице длины нерелаксированной границы. Время процесса фасетирования составляет
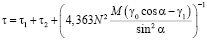 . (6)
. (6)
В случае границы, имеющей компоненты наклона и кручения (общего типа) необходимо рассматривать зародыш в виде пирамиды с треугольным основанием. Выражение [5] для энергии образования критического зародыша в форме правильной пирамиды:
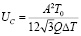 ,
,
где 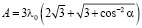 ;α – угол наклона грани пирамиды к основанию; T0 – равновесная температура перехода; ΔT – степень переохлаждения; Q – скрытая теплота перехода фасетирования на единицу площади исходной границы. Доля фасетированной площади границы ψ(t) к моменту времени t:
;α – угол наклона грани пирамиды к основанию; T0 – равновесная температура перехода; ΔT – степень переохлаждения; Q – скрытая теплота перехода фасетирования на единицу площади исходной границы. Доля фасетированной площади границы ψ(t) к моменту времени t:
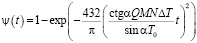 . (7)
. (7)
Общее количество фасеток на единице площади полностью фасетированной границе
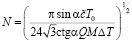 . (8)
. (8)
Величина 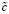 по-прежнему обозначает скорость образования зародышей, но теперь на единице площади границы. Поскольку процесс образования зародышей является термоактивационным, для оценки этой величины можно использовать выражение, подобное применяемому в теории кристаллизации:
по-прежнему обозначает скорость образования зародышей, но теперь на единице площади границы. Поскольку процесс образования зародышей является термоактивационным, для оценки этой величины можно использовать выражение, подобное применяемому в теории кристаллизации:
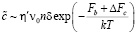 .
.
Здесьη’ – безразмерный коэффициент, 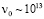 с-1 – частота Дебая, n – количество атомов в единице объема кристаллита, δ – толщина границы, Ub – энергия активации граничной самодиффузи. Оценка [5] времени τC появления зародыша дает
с-1 – частота Дебая, n – количество атомов в единице объема кристаллита, δ – толщина границы, Ub – энергия активации граничной самодиффузи. Оценка [5] времени τC появления зародыша дает
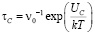 ,
,
а время всего фасетирования
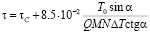 . (9)
. (9)
Переход границы к состоянию с более плотной упаковкой означает уменьшение объема, приходящегося на один атом 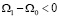 . Для фазового перехода первого рода, из формулы Клапейрона-Клаузиуса имеем:
. Для фазового перехода первого рода, из формулы Клапейрона-Клаузиуса имеем:
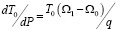 ,
,
где q<0 – скрытая теплота перехода, приходящаяся на один атом. Отсюда следует, что
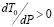 .
.
Это означает увеличение температуры перехода с повышением давления, что соответствует принципу Ле-Шателье.
Равновесная концентрация фасеток на границе [6] находится из условия минимума свободной энергии системы:
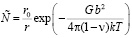 , (10)
, (10)
где 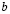 – величина порядка трансляции решетки зернограничных сдвигов; G – модуль сдвига;
– величина порядка трансляции решетки зернограничных сдвигов; G – модуль сдвига; 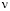 – коэффициент Пуассона;
– коэффициент Пуассона; 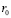 – размер ядра линейного дефекта сопряжения фасеток (порядка
– размер ядра линейного дефекта сопряжения фасеток (порядка 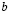 );
); 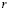 – величина порядка половины размера фасеток. Средний размер фасеток равен:
– величина порядка половины размера фасеток. Средний размер фасеток равен:
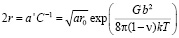 , (11)
, (11)
где 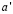 – период решетки совпадающих узлов.
– период решетки совпадающих узлов.
Заключение
Экспериментально наблюдаемые размеры фасеток изменяются в довольно широких пределах. Их размеры могут быть такими, что их можно видеть в световой микроскоп (0,01 – 1 мм ) – макрофасетки, или с помощью электронного или полевого ионного микроскопа (до нескольких десятков ангстрем) – микрофасетки. Это согласуется с оценками, сделанными по выражениям (5) и (8). Для времени фасетирования можно получить оценки в пределах 104 – 10–6 с. Такой разброс времён релаксаций соответствует иерархии в размерах и расположении фасеток [7], а также существенному различию в атомной структуре исходных нефасетированных границ.
Большая часть имеющихся литературных данных о структуре фасетированных границ относится к специальным границам. В несколько меньшей степени фасетированию подвержены границы общего типа с так называемой несоразмерной структурой. В результате образуются фасетки, атомная структура которых образована сопряжением плотноупакованной и атомно рыхлой граничными поверхностями кристаллитов [8].
Описанный механизм фасетирования межзеренных границ имеет общий характер. В каждом конкретном случае необходимо рассматривать кристаллогеометрические параметры границы.
Библиографическая ссылка
Кульков В.Г. КИНЕТИКА ФАЗОВОГО ПЕРЕХОДА ФАСЕТИРОВАНИЯ МЕЖЗЕРЕННЫХ ГРАНИЦ // Международный журнал прикладных и фундаментальных исследований. 2016. № 12-2. С. 233-236;URL: https://applied-research.ru/ru/article/view?id=10813 (дата обращения: 03.03.2026).

