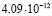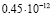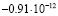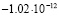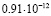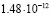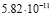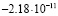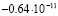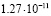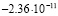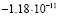Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Приходовский М.А. 1

---

1 ГОУ ВПО «Томский государственный университет систем управления и радиоэлектроники»

Предлагается новый вариант экстраполяционного численного метода Ричардсона. Предлагаемый метод отличается от исходного метода тем, что последовательность значений, соответствующих разному шагу, анализируется вероятностным способом. Вместо выбора одной подпоследовательности и нахождения её предела, как в методе Ричардсона, выбирается несколько непересекающихся подпоследовательностей, предел каждой из них ассоциируется с одним из значений случайной величины, и вычисляется математическое ожидание этой случайной величины. Это повышает достоверность результата, находимого численным методом. Доказано, что при n > 2, достигается точность больше, чем при n равном 2. Предложенная модификация может быть применена для более точного решения различных физических, в том числе астрономических задач, связанных с движением спутников и астероидов.

Статья в формате PDF

1475 KB

экстраполяция

приближённые вычисления

математическое ожидание

метод Ромберга

метод Ричардсона

1. Richardson L.F. Philos. Trans. Roy Soc. Ser.A, 1910, v.210, p.307–357.

2. Romberg W. Kgl norske vid. selskabs forhandl. 1955, Bd 28, №7, p.30–36.

3. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М., 2003. – 632 c.

4. Авдюшев В.А. Численное моделирование орбит: Монография. – Томск: Нац. исслед. Томский гос. ун-т, 2010.

5. Приходовский М.А. Математическое моделирование структурных изменений орбит спутников астероида при сближении с планетой // Успехи современного естествознания. – 2014. – № 12–2. – С. 68–74.

При решении тех или иных физических задач численным методом, производится конечная серия вычислений с шагом h. Естественно, что при уменьшении шага h получается более точный результат. Пусть результат, полученный численным методом в некоторой требуемой точке, обозначен T(h). Наилучший результат был бы достигнут при 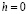. Однако выполнить такую серию вычислений физически невозможно, так как при этом получилось бы бесконечное число шагов. Тем не менее, значение 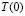теоретически может быть найдено. Существует класс экстраполяционных методов, начальная идея которых принадлежит Ричардсону [1]. Для вычисления определённых интегралов применяется метод Ромберга, являющийся адаптацией метода Ричардсона для этого класса задач [2, 3]. Метод Ричардсона активно используется и в астрономии для численного определения орбит небесных тел [4]. Технология экстраполяционных методов состоит в следующем. Вычислив T(h) для нескольких значений h, можно приближённо найти функцию T(h) (например, как интерполяционный многочлен Лагранжа) и затем вычислить предел 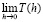, т.е. фактически, значение T(0), которое является гораздо более точным по сравнению с любым значением, полученным ранее при любом шаге h, так как соответствует «бесконечной» серии вычислений с нулевым шагом. Экстраполяция по n означает, что рассматривается предел 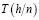при 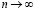. Поэтому метод называется экстраполяционным.

Одной из модификаций данного метода является экстраполяция при половинном делении шага на каждом последующем этапе. Вычислив T(h), затем поделим величину шага пополам и, выполнив 2 последовательных вычисления, найдём 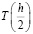, затем аналогично каждый отрезок делится ещё на две части, шаг становится 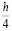, выполняется 4 последовательных вычисления, тем самым находится 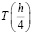, затем таким же способом 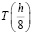и так далее. С каждым разом значение всё ближе к точному значению искомой функции в требуемой точке. Если таким образом измельчать разбиение множество раз, получится последовательность

.

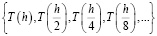Пусть через I обозначен точный результат, полученный аналитическим способом. Очевидно, что

.

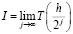Обозначим для удобства работы с последовательностями,

.

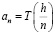Фактически, при последовательном половинном делении шага в методе Ричардсона, рассматривается не вся последовательность 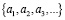, а лишь одна её подпоследовательность .

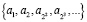Серии вычислений методом Ричардсона можно представить с помощью схемы (рис. 1).

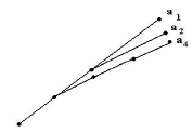
Рис. 1

Эта последовательность обладает свойством: разности 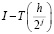между её элементами и предельным значением близки к некоторой бесконечной убывающей геометрической прогрессии. Почему это именно так, становится понятно из следующих рассуждений. Если точность исходного численного метода без экстраполяции была такова, что порешность пропорцональна 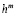, то погрешность с каждым новым шагом уменьшается в 2m раз, а именно 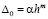, , 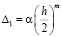, 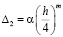... Таким образом, если каждый из знаменателей здесь имеет вид 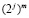, что равно 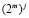, то погрешность близка к убывающей геометрической прогрессии со знаменателем 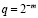. В частности, если точность исходного метода, к которому применяют асимптотический переход, есть 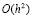, то погрешность

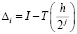
будет уменьшаться приблизительно в 4 раза при каждом следующем половинном делении шага, если 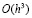то в 8 раз.

Остановимся подробнее на методе Ромберга. Если вычислить определённый интеграл с шагом с шагом 2h (обозначим полученный результат 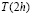), затем удвоить количество узлов и вычислить с шагом h (обозначим результат T(h)), то получим более точное значение. Причём если отклонение от точного значения ведёт себя как убывающая геометрическая прогрессия, то

.

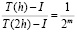Из этого следует, что

,

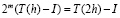а значит, в качестве асимптотического значения принимается следующее:

.

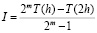Более точное приближение получится, если удвоить количество узлов не один, а несколько раз. Применяются следующие квадратурные формулы:

.

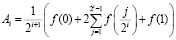Затем находятся элементы 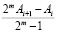. При этом требование на гладкость функций следующее: предполагается, что если число узлов удваивается n раз, то существует непрерывная производная .

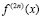Если погрешность есть функция вида 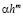, то при вычислении последовательности значений, их отклонение от точного результата есть геометрическая прогрессия со знаменателем 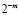. Так, при применении метода трапеций, погрешность имеет порядок 2 относительно h, соответственно, при каждом последующем половинном делении и удвоении количества узлов, результат в 4 раза ближе к точному значению интеграла. Строение последовательности 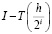близко к геометрической прогрессии, именно этим фактом и пользуются при применении метода Ромберга для экстраполяции.

Постановка проблемы

Вообще, если бы погрешность 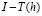в точности совпадала степенной функцией 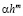, то было бы достаточно вычислить величину 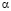из соотношения

,

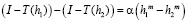получили бы

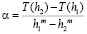
и тогда можно было бы принять в качестве значения интеграла величину

.

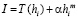Однако проблема в том, что погрешность 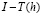не совпадает с 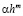, величина 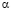зависит от h, не является постоянной, то есть

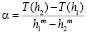
зависит от того, разбиения с какими шагами h1 и h2 сопоставляются. В связи с этим, вообще говоря, величины, рассматриваемые в методе Ромберга, также не образуют в точности геометрическую прогрессию, а значит, применение формул геометрической прогрессии при этом приводит к некоторой дополнительной погрешности, связанной с вариациями величины 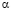. Точная геометрическая прогрессия получается лишь в том случае, если исходная функция является многочленом. Для тригонометрических функций, к примеру, получаем такие значения:

;

;

;

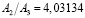
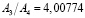
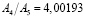
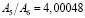
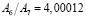
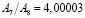
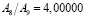
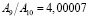
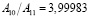
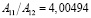
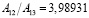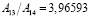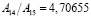При достаточно большом количестве узлов, например 215, на результат начинают сильно влиять ошибки, связанные с вычислительной техникой и ограниченностью разрядной сетки. Выбор оптимального шага и количества узлов, вообще говоря, является одной из открытых проблем.

Изучим подробнее, как может влиять нестационарность 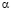на результат. Обозначим максимальное отклонение величины 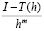от величины 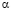через 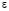, то есть 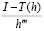принимает значения от 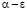до 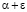. Тогда отношение двух таких величин заключено в границах от 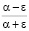до 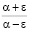. Таким образом,

,

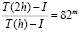где .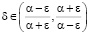

Если бы отклонение от точного значения при удвоении числа узлов вело бы себя в точности как геометрическая прогрессия, то было бы 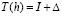, , 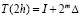где через 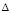обозначено отклонение результата, полученного численным методом при шаге h, от точного значения, то есть 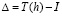. То есть, I есть значение, получаемое методом Ромберга, в предположении, что 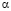величина постоянная и отклонения от точного значения уменьшаются со скоростью геометрической прогрессии.

Однако в действительности отклонение при предыдущем количестве узлов достигает не 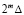, а 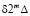, то есть верно отношение

,

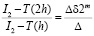где через I2 обозначен точный результат. Тогда

,

,

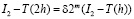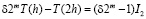следовательно,

.

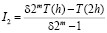Далее, выразим 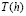и 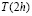через значение I, которое получалось бы при отсутствии вариаций величины 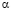, с целью выразить I2 через I и узнать, какая добавка получается из-за вариаций .

=

= =

==

= .

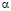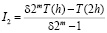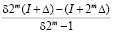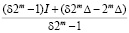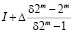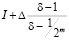Так, например, при использовании в качестве первичного метода трапеций (погрешность порядка h2, m=2) при асимптотическом переходе дополнительная погрешность, связанная с нестационарностью 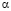, составит .

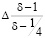Если 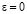(соответственно, 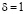) то величина

.

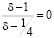Однако для реальных задач, где интегрируемая функция отличается от многочлена, величина 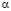зависит от h и не является константой. Поэтому при асимптотическом приближении с помощью формул геометрической прогрессии, нельзя ожидать точного результата, ведь на самом деле исследуемая последовательность отклоняется от прогрессии. В этом заключена некоторая неустранимая погрешность, связанная с самим рассматриваемым методом. Далее ищутся способы возможной минимизации этой погрешности.

Предлагаемая модификация метода

В связи со всем сказанным ранее, возникает необходимость усиления достоверности получаемого результата. Для этого может рассматриваться следующая идея: вместо экстраполяции на основе одной лишь только подпоследовательности, получить подобные результаты для серии из нескольких непересекающихся подпоследовательностей. Вообще, для всякого 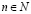, при разбиении отрезка длины h на n частей, всякий раз получается некоторое значение численного эксперимента, проводимого с шагом 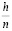, то есть существует общая последовательность значений

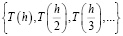
для всех натуральных чисел. Последовательность, применяемая в методе Ричардсона (и в частности, методе Ромберга) является лишь одной из её подпоследовательностей, а именно, с номерами 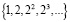. Очевидно, 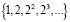не является единственной подпоследовательностью в N. В связи с этим закономерен вопрос, получится ли более точное решение при уменьшении шага на каждом этапе не в 2 раза, а в k раз, где 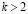. Можно рассматривать подпоследовательность номеров 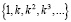в N и соответственно, последовательность результатов, полученных численным методом

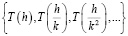
для различных чисел k. Назовём такое k базовым числом. В методах Ричардсона и Ромберга базовое число было равно 2. В общем же случае будет вычисляться предел вида 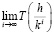. Множество значений, полученных с помощью экстраполяции при различных базовых числах, можно рассматривать как случайную величину, которая, в свою очередь, характеризуется математическим ожиданием и дисперсией. В методе Ричардсона и соответственно, Ромберга, рассматривается лишь одно значение случайной величины. Надёжность и достоверность результата повысится, если вместо одного экспериментально вычисленного значения рассматривать математическое ожидание нескольких найденных значений, рассматриваемых как значения некоторой случайной величины. Можно принимать в качестве результата среднее арифметическое асимптотических значений, полученных при различных базовых числах k.

Использование нескольких серий вычислений и поиск среднего арифметического являются способом дополнительного увеличения надёжности. Однако сначала докажем, что даже простая замена 2 на k может несколько улучшить результат.

Если бы погрешность при каждом последующем удвоении числа узлов была в точности геометрической прогрессией, то выполнялись бы равенства:

, ,

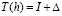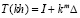где 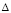– отклонение результата, полученного численным методом при шаге h, от точного значения, то есть 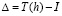. Однако на самом деле, значение 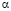подвержено некоторым вариациям, и максимальное отношение было обозначено через 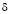. Поэтому

,

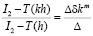где 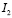точный результат. Тогда

,

,

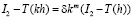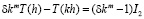следовательно,

=

= =

==

=.

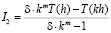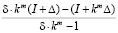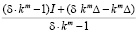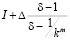Если погрешность первичного метода (без асимптотического перехода) порядка h2, то дополнительная погрешность, связанная с нестационарностью 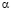, составит 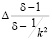. На следующем чертеже показан график величины .

При 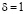эта величина равна 0, так как в этом случае 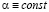. При 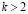отклонение меньше, а при k=2 наибольшее. Таким образом, использование k вместо 2 в методе Ромберга несколько лучше нивелирует нестационарность коэффициента 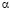, то есть уменьшает влияние отклонения рассматриваемой последовательности от геометрической прогрессии.

Так как при каждом последующем уточнении будет происходить увеличение количества узлов в k раз вместо удвоения, то в предлагаемой модификации метода должны использоваться следующие квадратурные формулы

,

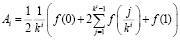где для простоты и наглядности записи взят промежуток 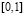. Асимптотические приближения в этом случае находятся по формулам

.

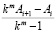Вычислительные эксперименты. Взаимосвязь базового числа k и количества шагов n

Предлагаемая модификация была проверена на различных задачах, связанных с вычислением определённых интегралов. Данный класс задач является хорошим материалом для отработки и совершенствования численных методов и их различных модификаций, потому что в таком случае известно точное решение, то есть некая эталонная функция, значение которой можно сравнивать с результатами, полученными численным методом. Таким путём можно исследовать сходимость самого метода. Затем разработанные методы могут быть использованы в реальных физических и астрономических задачах, где заранее известного аналитического решения нет.

Если проводится серия вычислений при нескольких значениях k, это позволяет вычислить среднее арифметическое. Такой подход повышает надёжность вычислений и исключает некоторые вычислительные ошибки, которые могли бы возникать при рассмотрении только одного базового числа k=2.

Применение к интегралам

В следующем примере показана разница между значением, вычисленным с помощью модифицированного метода Ричардсона при разных базовых числах, и точным значением, для определённого интеграла от рациональной дроби

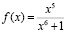
на отрезке [0,1].

Среднее арифметическое имеет погрешность около 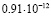. Значение, полученное для базового числа 2, является наиболее далёким от среднего арифметического. Таким образом, даже просто замена 2 на k, может помочь улучшить результат. Но ещё более значительное улучшение получается при сопоставлении вычислений, выполненных для нескольких значений k. Если же после серии экспериментов исключить одно значение, самое удалённое от среднего арифметического, можно дополнительно уменьшить дисперсию рассматриваемой случайной величины. Если исключить 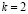, то получим «улучшенное среднее» с погрешностью всего лишь 0,23*10–12.

Замечание. Допускается также применение метода к вычислению неопределённых интегралов: по существу, здесь действует тот же самый метод Ромберга, что и для определённого интеграла, однако применяется к каждому отрезку [0,x]. Таким образом, можно найти интеграл

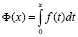
с переменным верхним пределом, где 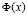есть первообразная функции f(x).

Возможно также применение метода к дифференциальным уравнениям. Показано на примере дифференциального уравнения 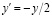. Программа вычисляет экстраполяционные приближения y(x) для значения x=1 при различных значениях базового числа k от 2 до 7, и сравнивает с точным решением.

К вопросу о выборе оптимального шага и количества узлов. Естественно, возникает вопрос, до каких пор нужно увеличивать количество узлов в k раз, какое количество n таких шагов является оптимальным. Очевидно, что мы не можем бесконечно измельчать шаг, так как ограничены вычислительными возможностями компьютерной техники, а также разрядной сеткой. Предлагается принять в качестве критерия выбора n достижение наилучшего сгущения значений, то есть производить измельчение разбиения до того момента, пока верно неравенство 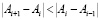. Таким образом, программа автоматически остановит процесс разбиения, когда начнут нарастать ошибки, связанные с чрезмерно большим количеством узлов.

Для сравнения, в следующей таблице показано поведение погрешности вычисления определённого интеграла от тригонометрической функции на отрезке [0,1] при различных k и n. Погрешность выражена в единицах 10–9, округлено до 10–11. Пустые клетки соответствуют ситуациям, когда отклонение стало меньше 10–11, либо процесс был остановлен из-за достижения оптимального n.

Для достижения сопоставимого уровня точности при большем k требуется меньшее n. Таким образом, замена базового числа 2 на другое k имеет смысл.

Заключение

В данной статье предлагается следующая модификация алгоритма Ричардсона. Предлагается рассматривать базовое число 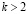вместо 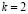, то есть работать с последовательностью вида

.

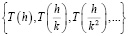Рассматривая серию экстраполяционных процессов при нескольких k, найти среднее арифметическое (это можно рассматривать как математическое ожидание случайной величины, вычисленное по выборке из нескольких значений). Возможно дальнейшее развитие этого метода, а именно, реализация вычисления улучшенного среднего значения, с исключением одного, являющегося самым удалённым от среднего арифметического. Предложенная модификация может быть применена для более точного решения различных физических, в том числе астрономических задач, связанных с движением спутников и астероидов, однако это выходит за рамки данной статьи.

Библиографическая ссылка