Современные задачи электроэнергетики предъявляют высокие требования, которые в первую очередь обосновываются появлением передовых алгоритмов релейной защиты и автоматики, базирующихся на явлении конечной скорости распространения высокочастотных волновых процессов в многопроводных линиях. Параметры воздушных линий электропередачи используются алгоритмами многих устройств релейной защиты и автоматики, следовательно, правильное их определение необходимо для обеспечения корректного функционирования систем релейной защиты и автоматики. Как правило, при определении продольных и поперечных параметров ВЛЭП используют усредненные данные, которые предполагаются неизменными, такие как проводимость грунта, физические свойства фазных проводников, атмосферные условия и геометрическое расположение фазных проводников относительно поверхности земли и друг друга. Следовательно, УРЗА могут функционировать не корректно (сработать ложно или излишне, или не верно определить расстояние до места повреждения), если их уставки не отражают реального состояния контролируемой ВЛЭП. Погрешность в расчётах по упрощенным формулам для модулей взаимных сопротивлений около 20%.
Удельное активное сопротивление определяется сечением проводника и удельным сопротивлением материала. Данные приводящиеся в справочной литературе рассчитаны на температуру провода 20°С не учитывают сезонные изменение температуры окружающей среды, присущие практически для большей части РФ.
Зависимость активного сопротивления от температуры провода определяется:
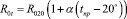 (1)
(1)
где R020 – табличное значение удельного сопротивления при температуре провода 20°С; tпр – температура провода, °С; α – температурный коэффициент электрического сопротивления, Ом/град.
Температура проводов воздушной линии электропередачи зависит от условий охлаждения в окружающей среде (температуры воздуха) и протекающего по ним тока. При предельных по условиям нагрева токовых нагрузок температура провода может достигать +70°С, а при низкой температуре окружающей среды и малых нагрузках до - 50°С, следовательно, удельное активное сопротивление может увеличиться на 20% и уменьшиться на 30%.
Из условия равновесия определяется установившиеся температура провода при любом режиме работы воздушной линии:
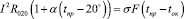 (2)
(2)
где I – ток проходящий про проводу, А; σ – коэффициент теплоотдачи, равный количеству тепла, отводимого в 1 сек с 1 см2 поверхности провода при разности температур провода и окружающей среды в 1°С, Вт/м2 . град; F – поверхность охлаждения провода, см2; tок – температура окружающей среды, °С. Коэффициент теплоотдачи, имеющий две составляющие, одна из которых определяется отдачей тепла лучеиспусканием σ?л), вторая — конвекцией (σк).
Количество передаваемой теплоты при лучеиспускании пропорционально разности абсолютных температур в четвертой степени. Коэффициент теплоотдачи лучеиспусканием определяется по формуле Стефана-Больцмана:
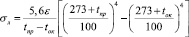 (3)
(3)
где ε – постоянная лучеиспускания (степень черноты провода).
Постоянная лучеиспускания может изменяться в широком диапазоне, так как зависит от состояния поверхности проводника, так для чистого алюминия она составляет 0,11, а для загрязненного или окисленного до 0,8.
Коэффициент теплоотдачи посредством конвекции, можно определить, если рассматривать воздушную линию электропередачи как гладкий цилиндр, с учетом того, что при малых скоростях ветра витая структура не влияет на теплоотдачу:
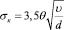 (4)
(4)
где υ — скорость движения воздуха около провода, м/сек; d — диаметр провода, м; θ – коэффициент зависимости теплоотдачи при конвективном теплообмене от угла атаки ветра.
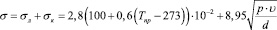 (5)
(5)
где р – давление воздуха, Па; Тпр – температура провода, К.
Коэффициент теплоотдачи может быть определен как[1]:
Из выражений следует, что на температуру провода оказывают влияние только скорость ветра, величина тока, проходящая по линии и температура окружающей среды.
С учетом выражения (5) найдем из уравнения (2) температуру провода воздушной линии:
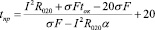 (6)
(6)
Построим на основании выражения (6) зависимость температуры провода А С -120 от температуры окружающего воздуха, скорости ветра и протекающего по нему тока (рис.1), учитывая атмосферное давление равное 1, температуру окружающей среды в диапазоне то +40°С до -40°С, скорость ветра от 0,6 м/сек, соответствующую перемещению воздушных масс только за счет нагрева до 6 м/сек. Так как Iдоп – это величина тока проходящая по воздушной линии при нормальной температуре (+25°С) и при отсутствии ветра, способная произвести нагрев провода до предельно допустимого значения (+70°С), то влияние токовой нагрузки оценивалось в диапазоне от 0 до Iдоп.
Из рис.1 следует, что при малых и средних токах от допустимого, проходящих по воздушной линии и не больших ветровых значительные изменения температуры провода происходят в основном из-за колебания температуры окружающей среды. Если токовая нагрузка более 30% от допустимого тока линии и скорость ветра не велика, то уже ток, проходящий по проводнику оказывает заметное влияние на его нагрев [2]. При увеличении скорости ветра значительно улучшается отвод тепла даже при большом значении протекающего тока (рис.2).
Исходя из зависимостей, представленных на рис. 1 и 2 следует, что температура проводника не опускается ниже -40 0С и не поднимается выше 79 0С, даже при малой скорости ветра и токе проходящему по линии равному току допустимому, следовательно, произведем анализ зависимости сопротивления провода воздушной линии электропередачи от температуры R0t=f(t) в указанном диапазоне (рис. 3).
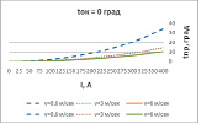
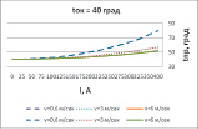
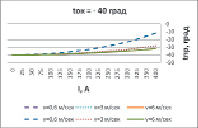
Рис. 1. Зависимости температуры провода марки АС-120 от протекающего тока, температуры окружающей среды, скорости ветра
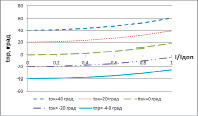
Рис. 2. Зависимости температуры провода воздушной линии электропередачи от температуры окружающей среды при средней скорости ветра (υ = 2 м/сек)
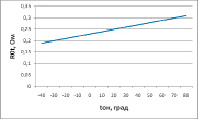
Рис. 3. График зависимости сопротивления провода марки АС-120 длиной 1 км от температуры окружающей среды
Из графика видно, что повышение температуры провода на 100С приводит к увеличению сопротивления провода на 4%.
Анализ температурных условий работы проводов различных сечений, используемых на воздушных линиях напряжением 35 кВ и выше показал, что основные зависимости температуры провода от протекающего тока, температуры окружающей среды, скорости ветра аналогичны представленным на рис.1. Следовательно, и зависимость сопротивления провода воздушной линии электропередачи при изменяющейся температуре окружающей среды для различных марок проводников не будет отличаться от графика представленного на рис. 3.
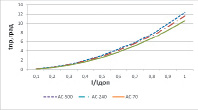
Рис. 4. Зависимость температуры проводов марок АС-500, АС-184, АС-70 от протекающего тока, температуры окружающей среды tок = 00С, скорости ветра 4 м/сек
Библиографическая ссылка
Ахмедова О.О. УТОЧНЕННЫЙ АЛГОРИТМ РАСЧЕТА АКТИВНОГО СОПРОТИВЛЕНИЯ ВОЗДУШНОЙ ЛИНИИ ЭЛЕКТРОПЕРЕДАЧИ С УЧЕТОМ ПОГОДНЫХ УСЛОВИЙ // Международный журнал прикладных и фундаментальных исследований. 2016. № 12-3. С. 387-389;URL: https://applied-research.ru/ru/article/view?id=10844 (дата обращения: 25.12.2025).

