Реальные межзёренные границы достаточно редко бывают плоскими в микромасштабе. Они обычно содержат различные отклонения от плоской конфигурации, включая в себя сильно искривлённые участки, изломы, фрагменты с другой ориентацией, имеют развитый неровный рельеф. Многообразие конфигураций такого рода границ обозначается [1] как ступенчатые, искривлённые, фрагментированные, изрезанные, с микрогранями, зигзагообразные, зубчатые, гофрированные, фрактальные, волнообразные, фасетированные. Истинное строение границ может иметь такого рода нерегулярности в одном или в двух измерениях границы. Среди различных физических механизмов образования таких границ можно выделить две группы. Одна включает механизмы, основанные на процессах, проходящих при стремлении системы к равновесию, к другой относятся те, которые протекают в существенно неравновесных условиях. Движущей силой первой группы является уменьшение свободной энергии системы. Образование фасетированной структуры является зернограничным фазовым переходом первого рода. Его механизмы для различного типа границ были достаточно подробно рассмотрены в работах [1, 2].
Межзеренное скольжение представляет собой взаимное движение зерен вдоль общей границы раздела. Такое движение является консервативным процессом только если межзеренная граница является плоской. В остальных случаях, когда граница искривлена, содержит уступы или фасетирована, движение консервативным не является. Это означает, что такое движение зерен обусловлено переносом вещества диффузионным путем либо между различными участками самой границы, либо между границей и объемными источниками или стоками.
Настоящая работа посвящена описанию механизмов проскальзывания по границам, имеющим различно ориентированные фасетки или ступеньки под действием приложенного извне напряжения.
Модели проскальзывания вдоль одномерно фасетированных границ
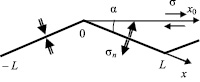
Рис. 1. Одномерно фасетированная граница
Рассмотрим симметричную одномерно фасетированную границу [3], изображенную на рис. 1. Она представляет собой цилиндрическую поверхность с направляющей ломаной линией, содержащей одинаковые звенья длины L, и образующей, нормальной к плоскости рисунка. Пусть в системе действует внешнее сдвиговое напряжение σ вдоль усредненной плоскости границы, обозначенной направлением оси x0. Граничная поверхность гофрирована с углами наклона плоских сегментов ±σ к оси x0. На каждом таком сегменте имеется нормальная компонента напряжения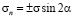 
, обозначенная на рис. 1 двойными стрелками. Совместим с отрезком ломаной ось x так, чтобы его концы соответствовали координатам 
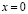и 
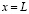. Нормальные напряжения чередующихся знаков на сегментах приводят к аналогичному изменению химических потенциалов вакансий. В системе нарушается равновесие, что вызывает их диффузионные потоки между соседними сегментами. Избыточная в сравнении с равновесной концентрация вакансий Cb в границе в отсутствие потоков
.
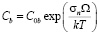При условии малости напряжений
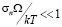
она равна
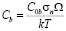. (1)
Здесь C0b – равновесная концентрация вакансий в границе, Ω – атомный объём. На сегментах происходит генерация и поглощение вакансий. Возникающие диффузионные потоки приводят к массопереносу, и следовательно, к взаимному движению зёрен. Вследствие очевидной симметрии достаточно рассмотреть только один сегмент, изображенный на рис. 1. Симметрия задачи приводит к нулевым граничным условиям для избыточной концентрации на границах сегмента.
Решение стационарного неоднородного уравнения диффузии
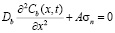(2)
имеет вид [4]:
, 
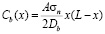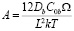. (3)
Здесь коэффициент A пропорционален мощности источника вакансий, Db – их зернограничный коэффициент диффузии. Выражение (3) получено с учетом т.н. эффекта подстройки напряжений. Он заключается в том, что установившееся распределение вакансий на сегменте пропорционально распределению на нем нормальных напряжений. При этом соблюдается равенство полной силовой нагрузки на сегменте со стороны внешнего напряжения и напряжения, распределенного по сегменту
.
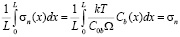Баланс генерации и потоков вакансий приводит к результирующему выражению для скорости межзеренного проскальзывания
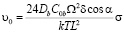. (4)
Учет диффузионных потоков из границы к объемным стокам в [5] зерне приводит к выражению
,
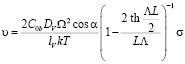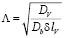, (5)
где DV – коэффициент объёмной диффузии вакансий; lV – средняя длина пробега вакансий из границы в объём; δ – диффузионная толщина границы.
Двумерно фасетированная межкристаллитная граница представляется рельефной поверхностью с пирамидальными выступами по обе стороны от нее. Проскальзывание по границе с симметричным строением, когда в основании пирамид лежат равносторонние треугольники, а угол наклона фасеток к средней плоскости границы таков, что они являются квадратами, осуществляется путем диффузионного перераспределения вакансий между областями границы с растягивающими и сжимающими нормальными напряжениями.
Задачу можно считать [4] квазиодномерной. Решение уравнения диффузии приводит к результату:
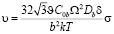, (6)
где b – сторона квадратной фасетки, а геометрический коэффициент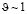 
.
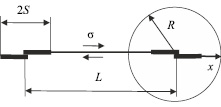
Рис. 2. Ступенчатая граница
Представляет интерес рассмотрение границы, содержащей ступеньки малого размера, соединяющие между собой протяженные плоские сегменты (рис. 2). Такая конфигурация является предельным случаем строения фасетированной границы, когда плоскость исходной нефасетированной структуры располагалась под малым углом к плотноупакованным плоскостям решетки совпадающих узлов, либо была ей параллельна. Эффективное напряжение сжатия или растяжения на ступеньке равно
,
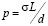где d – ее высота. Вакансии поддерживают квазиравновесие с их источником (ступенькой) на расстоянии S. Величину S можно определить как среднеквадратичное расстояние, доступное для вакансии за время τ, пока она не испарится в объём.
,
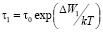где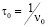 
, ν0 – характерная частота колебаний атомов (порядка дебаевской); ΔW1 – энергия активации движения вакансий из области границы в объём. из соотношения Эйнштейна имеем
.
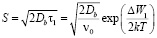В случае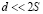 
ступеньку с прилегающими к ней с двух сторон участками границы протяженностью S заменим плоским источником ширины 2S с концентрацией вакансий в нём 
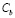. Такой источник имеет пластинчатую конфигурацию шириной 2S. Дальнейшее рассмотрение определяется соотношениями величин расстояния L между ступеньками в границе, расстояния R между ступенькой и вакансионными стоками в объеме зерна, а также ширины источника 2S (рис. 2). В связи с этим рассмотрим различные возможные ситуации [6].
1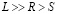 
. Задача решается в координатах эллиптического цилиндра с фокусами, расположенными на краях источника. Скорость определяется выражением
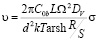. (7)
При выполнении соотношения R>>S (7) принимает вид
.
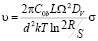2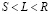 
. Имеем дело с диффузией в объеме зерна между положительным и отрицательным источниками вакансий. Такую конфигурацию по аналогии с дислокациями можно назвать диполем. Скорость определяется выражением:
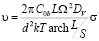. (8)
3. 
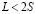. В этом случае вакансии движутся от источника к стоку вдоль границы, не успевая удалиться в объём. Уравнение Лапласа сводится к одномерному
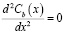
с граничными условиями:
.
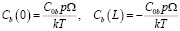Скорость, выраженная через потоки в обе стороны от ступеньки, даётся выражением:
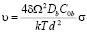. (9)
В предложенной модели считается, что скорость проскальзывания определяется процессами самодиффузии вблизи ступенек. Если скорость процессов атомных перестроек при скольжении по плоским участкам границы соизмерима со скоростью релаксации вблизи ступенек, то нужно также учитывать ее вклад. Из баланса сил заключаем, что величина внешнего напряжения σ равна сумме величин напряжения вязкого сопротивления проскальзыванию σ’ и напряжения от ступенек
,
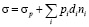где ni – количество ступенек величины di на единицу длины границы вдоль x. Первое слагаемое определяется выражением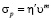 
, где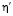 
– эффективная вязкость плоских участков границы, а m – скоростная чувствительность напряжения. Напряжение на ступеньке линейно связано со скоростью проскальзывания: 
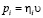с вязкостью 
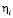. Тогда из баланса сил имеем
.
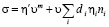Решив это уравнение относительно υ, можно найти скорость взаимного смещения зёрен. В зависимости от соотношения величин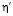 
и 
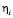скорость смещения зёрен определяется либо процессами на плоских участках, либо диффузионными процессами на ступеньках, либо вкладом обоих.
Превышение уровня растягивающих напряжений вблизи ступенек одного знака порогового значения может приводить к релаксации системы путем образования протяженной вдоль ступеньки цилиндрической поры [7]. Величина приложенного к границе порогового сдвигового напряжения
,
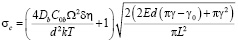где γ0 и g – удельные поверхностные энергии межзеренной границы и свободной поверхности поры; E – модуль Юнга; d – высота ступенек и диаметр поры; L – расстояние между ступеньками и чередующимися с ними порами.
Скорость проскальзывания определяется суммарным потоком вакансий к ступеньке из объема и вдоль границы:
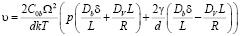. (10)
Сравнительная оценка слагаемых в (10) позволяет записать выражение для скорости проскальзывания в виде
.
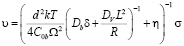Легко понять, что в таком процессе объем поры увеличивается [7] со скоростью
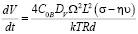. (11)
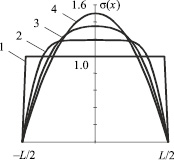
Рис. 3. Распределение вакансий на сегменте
Рассмотренные до сих пор процессы являлись стационарными, когда режим проскальзывания считался установившимся и в дальнейшем от времени не зависел. Интересно проследить за изменением основных параметров проскальзывания в зависимости от времени. С этой целью необходимо решить нестационарное уравнение диффузии вакансий с их источниками на фасетированной границе
.
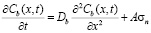Здесь обозначения такие же, как и в (2). Решение релаксационного уравнения для зернограничной концентрации вакансий для одного сегмента имеет вид
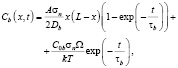(12)
где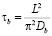 
– время релаксации. Численное решение нестационарного уравнения диффузии было получено в [8]. На рис. 3 представлен результат этого решения в виде графиков координатной зависимости концентрации вакансий на сегменте для различных моментов времени. Начальное распределение в момент приложения нагрузки обозначено цифрой 1, промежуточные – 2, 3 стационарное – 4. Как видно из рисунка стационарное распределение имеет параболическую форму, что согласуется с (12).
Нормальные компоненты напряжений на смежных фасетках имеют чередующийся знак. Химический потенциал примесных атомов на границе имеет различную величину, что приводит к перераспределению примеси между фасетками [9, 10]. В стационарном режиме проскальзывания наличие таких атомов приводит к изменению эффективной вязкости границ в консервативном процессе скольжения. В динамическом режиме, когда граница подвержена действию периодически изменяющегося сдвигового напряжения, процессы перераспределения примесных атомов могут привести к появлению пика внутреннего трения [11, 12]. Такой эффект проявляется в металлах с ультрамелким или наномасштабным размером зерен.
Заключение
Проскальзывание вдоль фасетированных границ зерен неизбежно связано с возникновением нормальных напряжений и диффузионных потоков вакансий между фасетками. Полученные выражения для разных конфигураций границ показывают, что величина скорости проскальзывания является линейной функцией приложенных напряжений. Так происходит, пока величина напряжений достаточно мала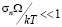 
. Рассмотрение больших напряжений требует использования экспоненциальной зависимости концентрации вакансий от напряжений, как это указывалось в тексте перед формулой (1). При таких напряжениях эффективность границ как источников вакансий ограничена. В связи с этим возникают нелинейные эффекты, и скорость перестает линейно зависеть от напряжений.
Нестационарный режим проскальзывания сразу после приложения постоянного напряжения является хорошей иллюстрацией принципа Ле Шателье – Брауна. Первоначальное ступенчатое напряжение на фасетках вызывает большие потоки вакансий, которые приводят к перераспределению как вакансий, так и напряжений на них. Такой эффект подстройки напряжений уменьшает отклик системы на внешнее воздействие путем снижения величины скорости проскальзывания.
Библиографическая ссылка
Кульков В.Г. МЕЖЗЕРЕННОЕ СКОЛЬЖЕНИЕ ПО ФАСЕТИРОВАННЫМ ГРАНИЦАМ В МЕТАЛЛАХ // Международный журнал прикладных и фундаментальных исследований. – 2017. – № 1-1. – С. 14-19;URL: https://applied-research.ru/ru/article/view?id=11085 (дата обращения: 23.11.2024).