Обучение понятиям – длительный процесс, который не завершается усвоением его определения, а имеет целью, прежде всего, включение понятия в систему действий по его использованию для изучения и описания объектов и явлений реального мира, в том числе и умственного мира учащихся, и, особенно, при решении ими различного рода задач. При этом математическое понятие выступает по большому счету в роли, с одной стороны, модели объекта познания, то есть, по нашим представлениям, служит его аналогом [5, 6], с другой – особенно в процессе обучения, само является объектом познания, то есть выступает для учащегося в роли оригинала. Эта двойственная роль математических понятий должна быть учтена при выстраивании методики обучения математическим понятиям с активным использованием аналогии.
Под методикой применения аналогии в процессе обучения понятиям будем понимать программу таких действий учителя и учащихся (умственных и материализованных) с понятиями, которая обеспечивает учащимся значительный уровень овладения ими, характеризующийся их пониманием, способностью осознанно применять их при решении задач и ориентироваться с их помощью в изменённых условиях. В такой программе действий может быть выделено и описано главное звено применения аналогии, определяющее направленность и основную цель этого процесса, а также – его отдельных этапов и действий, составляющих его структуру.
Главное звено использования аналогии
Формирование у учащихся понятий с использованием аналогии можно сравнить с процессом становления их в науке, если на ограничиваться лишь традиционно наблюдаемыми в обучении действиями по выявлению тех или иных свойств понятий, их пояснением со стороны учителя, усвоением определений и т.п. Например, понятие вектора как элемента векторного пространства сформировалось в науке в процессе выявления и обобщения аналогии между отдельными «представителями» вектора (как обобщенного понятия). Вначале – векторных величин в физике типа силы, перемещения, скорости, наряду с этим – их геометрическими образами в виде направленных отрезков, далее – переносами плоскости как особого рода отображениями, затем упорядоченными наборами чисел и т.д. Видимо, через средства, подобные отмеченным, и умственные действия с ними желательно провести и учащихся при формировании у них этого понятия, если при этом активно использовать аналогию.
Аналогия в этом случае используется как основание, во-первых, для установления особого рода сходства сложных объектов, каковыми являются отдельные «представители» общего понятия, и, во-вторых, для переноса полученной информации с отдельных «представителей» на это общее понятие. Последнее в процессе обучения играет для учащегося роль оригинала, то есть такого объекта математической теории, которое желательно сформировать у него с достаточной полнотой, ещё не поддающейся непосредственному восприятию. С точки зрения принимаемой и развиваемой нами трактовки аналогии [2, 5, 6] отдельные «представители» общего, формируемого у учащихся, понятия оказываются его аналогами, его моделями (относительно некоторого известного набора характеристик – базы аналогии [6]). Тогда основная цель применения аналогии – сформировать более полные представления о понятии-оригинале путём изучения-исследования его моделей и переноса обобщённой информации с моделей на оригинал, используя, в том числе, и базу аналогии. Эта совокупность действий, составляющих важный фрагмент умственной деятельности по использованию аналогии в процессе формирования математических понятий, и является его главным звеном. При этом, конечно же, необходимо учитывать и особенности различных моделей как более конкретных понятий или даже предпонятий, протопонятий [3], и взаимосвязи между ними и опыт «общения» с ними учащихся, и, наконец, средства наглядного представления и этих отдельных моделей, и действий с ними.
Рассмотрим в качестве примера изучение понятия степени с натуральным показателем в VII классе. Считается, что на этом этапе обучения данное понятие является усвоенным на достаточном уровне, если учащиеся:
– знают соответствующие определения и правила действий со степенями (см., например, действующий учебник [10] для n∈N – §4, для n = 0 – §8),
– умеют на этой основе раскрывать выражения вида an и вычислять их значения при различных а,
– умеют использовать эти знания и умения в тождественных преобразованиях выражений, необходимые при изучении многочленов.
И все же, овладевши только указанными знаниями и умениями, даже если они достаточно хорошо «отработаны» и закреплены, учащиеся часто допускают ошибки такого рода: нередко вместо 23, b5+x и т.п. они вычисляют 2•3, b(5+x) или b 5 + b x. Во многих методических пособиях [1, 11, 14] подобные ошибки объясняют так называемыми ложными (?) аналогиями. Надо полгать, что в этих случаях учащиеся усматривают некоторое сходство форм, то есть, вообще говоря, внешних свойств сравниваемых объектов. Для того чтобы в дальнейшем не впасть в путаницу понятий, будем называть такой тип сходства певдоаналогией, тем самым уже по названию отличая его от понятия аналогии как структурного сходства сложных объектов [6, с. 246]. Выявим далее глубинные причины возникновения этих и других ошибок, проанализировав понятие степени с натуральным показателем.
По определению bп есть результат арифметической операции возведения в п-ю степень числа b, то есть, при п>1 – результат умножения п одинаковых множителей, каждый из которых равен b: 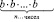 (В). Однако в младших классах учащиеся изучали действие (операцию) сложение п одинаковых слагаемых, каждое из которых равно а, а результат, то есть сумму
(В). Однако в младших классах учащиеся изучали действие (операцию) сложение п одинаковых слагаемых, каждое из которых равно а, а результат, то есть сумму 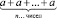 , записывали как произведение:
, записывали как произведение: 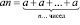 (А). Отметим, что именно с рассмотрения этого аналога начинается изучение понятия степени в учебнике [10, §4], что вполне методически оправдано.
(А). Отметим, что именно с рассмотрения этого аналога начинается изучение понятия степени в учебнике [10, §4], что вполне методически оправдано.
Чтобы использовать введенное в [2, 6] понятие аналогии, рассмотрим теперь два свойства: р1 – «для чисел выполняется некоторая (бинарная) операция» и р2 – «результат операции находится с помощью п одинаковых чисел». Совокупность этих двух свойств обозначим буквой S = {р1, р2}. Тогда, следуя [6, с. 246], относительно этого набора свойств понятия «степень bп» и «произведение а×n» необходимо признать аналогичными. Как правило, эту базу аналогии данных понятий с учащимся избегают выявлять. Им остаётся воспринимать внешнее сходство, псевдоаналогию изучаемых объектов – символических записей результатов соответствующих арифметических действий. Подмеченное и внешне воспринимаемое сходство форм учащиеся расширяют и неправомерно переносят его с формы записи на понятие как самой операции «возведение числа b в степень п», так и ее результата – степени bп. Такое сходство, подмеченное ими на уровне лишь протопонятий, и его неправомерный перенос на другие объекты, приводит учащихся к ошибкам. Причина, таким образом, не в аналогии как своеобразном отношении типа сходства между сложными объектами, а её неумелое использование. В частности, непонимание того, что математические понятия – это сложные объекты, на что и не обращают внимания ни в школе, ни – часто – и вузе. Таким образом, в процессе обучения степени необходимо обучать не только (и не столько) определениям понятий, в особенности аналогичных друг другу, но и осознанному и верному использованию отношения аналогии понятий. Более того, применение аналогии и обучение грамотному её использованию при освоении понятия степени (и не только его) становится необходимым элементом обучения самим понятиям – дорастанию их до понимания математического понятия как элемента теории, вбирающего в себя многие его аналоги как его модели. В силу сказанного, наш следующий шаг – выяснить те умственные действия и операции, которые составляют метод аналогий как метод познания и обучения математике и её важным компонентам – понятиям и задачам [6].
Одна из первых групп действий по использованию аналогии – подготовительные, обозначим их Дп. К ним мы отнесем Дп1 – формирование первичных представлений учащихся о понятии-оригинале и цели его исследования (ознакомление с ним). Следующие два действия этой группы Дп2, Дп3. – ознакомление учащихся с конкретными представителями, моделями-аналогами (их часто называют просто примерами) нашего оригинала и со сходством (аналогией) между ними как возможными средствами, которые будут использоваться для достижения поставленной цели. При этом предполагается, что учитель, организующий описываемый процесс, понимает, что аналогия трактуется как специфическое отношение сходства между оригиналом (познаваемым объектом) и его моделями-аналогами [6], и на достаточном уровне владеет этим понятием. Результатом выполнения подготовительных действий является учебная ситуация по применению аналогии для изучения с её помощью нового понятия.
После уяснения учащимися ситуации на обозначенном подготовительном этапе (через выполнение соответствующей системы подготовительных учебных заданий), процесс использования аналогии переходит во вторую стадию – реализующих действий Др. Одно из первых действий этой группы Др1 – выбрать из некоторого, предъявленного учащимся набора, модели, полезные для достижения цели, и исследовать их. Действие является необходимым: если нужные модели изучаемого понятия не будут найдены и осознаны учащимися, то не будет и оснований для вывода по аналогии. Следующие два необходимых действия (Др2, Др3) – исследование выбранных моделей оригинала и получение желательной информации о них и – через них – первичной информации об оригинале. Этап реализующих действий настолько важен, что, фактически, он и определяет главное звено применения аналогии – вывод по аналогии, трактуемый как перенос информации с моделей на оригинал [12]. Его можно представить в виде следующей схемы:
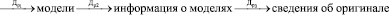
Прежде чем конкретизировать обозначенные действия, в особенности на примерах учебных заданий соответствующих типов, рассмотрим далее один из распространенных в математике видов аналогии понятий и способы его применения для получения соответствующих умозаключений. Продолжим для этого рассматривать понятие степени с натуральным показателем на множестве рациональных чисел (мы ограничиваемся этим множеством, поскольку в основной, да и в старшей школе им в большинстве случаев и ограничиваются авторы учебных пособий).
Некоторые математические основания аналогии понятий (комментарий для студентов, магистрантов, аспирантов и учителей)
Вернёмся к рассмотренному выше примеру изучения степени. В качестве оригинала, то есть изучаемого, а на начальном этапе формируемого понятия здесь целесообразно принять понятие (В) арифметического действия «возведение числа b в п-ю степень» как «умножения п одинаковых чисел», а в качестве его аналога – понятие (А) «сложение п одинаковых чисел, каждое из которых равно а». Проще всего аналогию между этими понятиями «увидеть», сравнивая две последовательности чисел и используя общепринятые символы для результатов рассматриваемых действий:
(А): а, а+а, …, 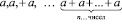 ;
;
или: а•1, а•2, … а•п;
(В): b, b•b, …, 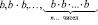 ;
;
или: b1, b2, …, bn.
Далее, введя в рассмотрение для чисел а и b (а ∈ Q, b∈ Q+) соответственно понятия «противоположный» и «обратный» элементы, можно по аналогии эти последовательности «дополнить» слева и получить:
(А′):...,(–а)•п, …, (–а)•2, (–а)•1, (–а)•0 = (–а)•(–а+а) = 0, а•1, а•2, … а•п, …;
(В′): 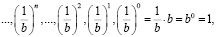 b1, b2, …, bn,…
b1, b2, …, bn,…
Иными словами, на самом деле речь идёт не столько об аналогии операций, сколько об аналогии действительно сложных математических объектов. На множествах Q рациональных чисел и Q+ – рациональных положительных чисел (b ≠ 0), отдельно друг от друга рассматриваются операции: на первом – обычная (бинарная) операция сложения и (унарная) операция перехода к противоположному числу (-а); на втором – обычное умножение и (унарная) операция перехода от числа b к обратному числу b-1. Тогда имеем две числовые системы ⟨Q, +, –, 0⟩ и ⟨Q+,•,-1, 1⟩ – алгебры, являющиеся, соответственно, аддитивной и мультипликативной группами рациональных (в случае Q+ – положительных) чисел [8].
Из университетского курса алгебры известно, что заданная на множестве Q функция, например y=f(x) = 2х, вместе с обратной функцией x = log2y осуществляют взаимно однозначное соответствие между указанными множествами, причем так, что сумме х1 + х2 чисел из Q соответствует произведение у1•у2 чисел из Q+, и наоборот. Следовательно, рассматриваемые группы изоморфны. С позиций введенного в [2, 5, 6] определения аналогии, наличие изоморфизма позволяет утверждать, что соответствующие группы и, как следствие, рассматриваемые на них операции аналогичны относительно рассмотренного выше набора их свойств S = {р1, р2}. Такое объяснение аналогии рассматривалось ещё известным математиком и ее популяризатором Д. Пойа [10].
Изоморфизм позволяет, расширить набор S еще двумя общими характеристиками р3 и р4. р3: «существует нейтральный элемент по соответствующей операции»: в Q им является число 0, в Q+ его роль выполняет число 1, то есть выполняются равенства: а + 0 = 0 + а = а и b•1=– 1•b= b, и р4: «для любого элемента из Q существует ему обратный по основной операции (то есть, в Q – противоположный), так что в Q выполняется равенство –а + а = 0, а в Q+ соответственно (b-1)•b = 1. Наконец, за счет изоморфизма элементу –а из Q соответствует в Q+ элемент 1/b= b-1, и наоборот. Становится понятным, почему произведению двух произвольных чисел из Q+ соответствует сумма их прообразов из Q. Например, во взаимно однозначном соответствии находятся такие элементы из рассмотренных выше последовательностей (А) и (В):
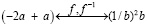 .
.
Всё это определяет аналогию понятий «сумма (произведение) одинаковых чисел» уже относительно пополненного набора характеристик S = {р1, р2, р3, р4}. Такова теоретическая основа рассматриваемой аналогии, которую учащиеся, фактически, обнаруживают на допонятийном уровне и которую целесообразно вывести на уровень их осознания и деятельности (возможно, не используя напрямую соответствующие термины). Опыт показывает, что это возможно, если последовательно и систематически следовать логике метода аналогий, о котором в [6, с. 253] было лишь упоминание, и провести учащихся через систему необходимых учебных заданий, побуждающих их использовать соответствующие средства аналогии и отражающих адекватные умственные действия.
Учебные средства применения аналогии
Чтобы аналогию, особенно в форме изоморфизма, можно было эффективно использовать в процессе обучения необходимо обратиться ещё к одной форме аналогии, возможно, наиболее распространенной и легче всего воспринимаемой. Такой формой, как с психологической и философско-математической точки зрения обосновано в [3, 5, 6, 13], является знаковое моделирование. Отсылая читателя к соответствующей литературе, отметим далее лишь те средства, которые активно и издавна (в особенности, со времен Р. Декарта) используются в математической познавательной деятельности. К таким моделям мы относим: предметно-образные, словесные, словесно-символические, изобразительные и символические [5].
Так, предметно-образными моделями понятий «произведение» и «степень» для учащихся, начиная с младших классов, могут служить соответствующие наборы хорошо известных им предметов. Например, «п наборов по а каких-то предметов в каждом наборе» является словесной моделью произведения а•п, запись а•п – его символическая модель, а конкретный набор трех коробок по 7 цветных карандашей в каждой – предметная модель произведения, передаваемая также в форме символической, но уже числовой модели: 7•3 = 7+7+7 (карандашей). Для понятия «степень с натуральным показателем» предметной моделью может служить нетрудно представляемый учащимися пример: на этаже школы имеется 7 одинаковых классных комнат, в каждой из них – 7 рядов, в каждом ряду по 7 столов; всего на этаже: (1 стол)•7•7•7 = 73 столов. В этом случае, последняя запись представляет собой символическую (числовую) модель понятия «степень числа 7 с показателем 3». Ей нетрудно сопоставить какую-то другую предметную модель, придавая основанию и показателю иные значения, воспринимаемые учащимися. Продолжая этот процесс, можно придти и к полнокровной словесной модели – определению более общего понятия «степень числа b с показателем n» и ввести для него соответствующую символическую модель bn.
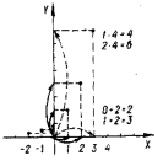
Рис. 1
Что касается изоморфизма выше представленных множеств (А) и (В), то для конкретных а и b (например, а = 1, b = 2) его можно дать в виде графика функции 2n (n∈Z) в системе координат хОу (рис. 1). На рисунке стрелочками по оси Ох иллюстрируется сложение и вычитание чисел из (А), на оси Оу – умножение и деление чисел из (В). Точками и штриховыми линиями на плоскости хОу изображается соответствие результатов этих действий при изоморфном отображении первого множества (А) на второе (В).
Так как знаковые модели являются аналогами формируемых понятий, то переходы от одного из них к другим, сопровождаемые соответствующими словесными переформулировками, представляют собой необходимые умственные действия по применению аналогии. Фактически, в таких переходах осуществляется перекодирование информации, ведущее к овладению различными моделями формируемого понятия и тем самым обогащающее его понимание учащимися. Очевидно, использование различных моделей, как и осуществление переходов между ними необходимо предусмотреть в соответствующей системе учебных заданий. Приведём примеры таких учебных заданий для учащихся V-VII классов, которые отвечают логике использования аналогии при формировании понятия степени вначале с натуральным, а затем и с целым показателем при положительном основании.
Учебные задания на применение аналогии
|
1) 4+4+4+4+4; |
4•4•4•4•4 |
|
2) a+a+a+a; |
b•b•b•b; |
|
3) 3x+3x+3x; |
3y•3y•3y; |
|
4) (c+b)+(c+b)+ (c+b); |
(x+y)•(x+y)•(x+y); |
|
5) (–a)+(–a)+(–a)+ (–a); |
|
1. Сравнение моделей и оригинала, выявление их общности. Перенос общего свойства на оригинал.
1) Что общего в построении сумм и произведений? При ответе на этот вопрос требуется, фактически, выявить общность хотя бы части из характеристик набора S = {р1, р2, р3, р4}. В особенности это касается р1, р2.
2) Как коротко записывается результат сложения в левой колонке? Предложите краткую запись произведений в колонке слева, воспользовавшись вашим опытом из младших классов. (Учитель убеждает в целесообразности общепринятой записи а•n, хотя учащиеся могут предложить другую.)
3) Опишите словами (устно или письменно), что предлагается сделать с числами или выражениями в каждой из колонок. Какое новое действие получают при сложении п одинаковых чисел, и как называют результат этого действия? Можно воспользоваться таким примером: «В выражении 5+5+5 предлагается сложить три одинаковых числа, то есть найти сумму таких чисел, каждое из которых равно 5. Такую сумму коротко записывают 5•3 и называют произведением числа 5 на число 3». В каких случаях пользуются таким действием? Приведите примеры. Охарактеризуйте с этих позиций сходные и отличительные признаки примеров в левой и правой колонках.
4) Что можно ожидать от умножения п одинаковых чисел? Что, по аналогии, можно и нужно изменить? Если перемножить три одинаковых числа, каждое из которых равно 5, то получим выражение 5•5•5. Короче оно записывается в виде 53, так что 5•5•5 = 53. Получаем третью степень числа 5, или говорят: «пять в третьей степени»; 5 – основание степени, число 3 – показатель степени. Действие «умножение п одинаковых чисел, каждое из которых равно b» – это есть новое действие, его называют возведением числа b в п-ю степень, результат этого действия называют п-й степенью числа b и всё это записывают так: 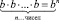 . В каких случаях удобно пользоваться этим действием? Приведите примеры, придумайте свои примеры.
. В каких случаях удобно пользоваться этим действием? Приведите примеры, придумайте свои примеры.
5) В чем сходство и отличие рассмотренных действий: в используемых основных исходных действиях? В словесном описании? В результатах?..
2. Различные знаковые модели оригинала и переходы между ними
1) На этаже здания имеется 5 одинаковых офисов, в каждом из них – 5 рядов, в каждом ряду по 5 столов; сколько всего столов на этаже? Запишите ответ с помощью: а) произведения чисел, б) степени числа.
(Ответ может быть дан в следующих записях: (1 стол)•5•5•5 = 53 (столов). Первое умножение отвечает на вопрос: сколько столов в одном ряду? Второе умножение – на вопрос: сколько столов в 5 рядах? И т.д.
2) Изобразите описанную или аналогичную ситуацию на рисунке.
3) Верны ли равенства: 3•2 = 2•3; 32 = 23? Как вы это объясните? Приведите свои примеры.
3. Использование изоморфизма на графической модели
Начертите параллельно друг другу две числовые оси Ох и Оу, отметив на них начало координат и единичный отрезок. На первой из них отметьте число 0 и ещё несколько целых чисел п справа и слева от него (|n|≥1, вначале берутся положительные числа). На второй оси отметьте числа 2n, проведите стрелочки от двух-трёх точек первой оси к соответствующим точкам второй оси. Полученное соответствие можно задать парами чисел: (0;1), (1;2), (2;4). Составьте ещё несколько пар соответствующих чисел.
В математике французским ученым Рене Декартом и его последователями был придуман удобный способ совместного рассмотрения 2-х числовых осей – известная вам декартова система координат ХОY. Будем изображать на горизонтальной оси ОХ целые числа п и их суммы. На вертикальной оси – числа 2п. Какие числа на оси ОY соответствуют суммам 1+2, 0+2, 3 – 2, 2 – 2, взятым на оси ОХ? Как эти числа можно записать в виде произведения соответствующих чисел? В виде степени? Какую закономерность вы подмечаете? Ответ запишите словами и символически, в общем виде.
Вспомним, каким общим законам подчиняются действия (операции) сложения и умножения. Запишем их в общем виде (символически), опишем их словами. А теперь сравним действия умножения и возведения в степень: какие общие законы (свойства) выполняются?
На основании каких законов и каких действий выполняются следующие преобразования (упрощения выражений):
а) a+b+a+a+b = 3a + 2b;
a·b·a·a·b = a3·b2;
б) (a + b)·c = ac + bc; (a·b)c = ac·bc?
Обоснуйте правильность последнего равенства, используя определение степени. Как бы вы назвали и сформулировали правило, которое задаётся этим равенством и которому подчиняется действие «возведение в степень с»? При каких условиях выполняются равенства п. б? Верно ли последнее равенство для любых a,b,с, а не только при a,b3 0, с ∈ N?
Отметим, что приведенные типы заданий для учащихся, фактически, побуждают их выполнять те умственные действия, которые закреплены в названиях этих заданий и выше (с. 4) определены как реализующие действия, составляющие главное звено метода аналогий. Впрочем, набор этих заданий требует существенного пополнения, если иметь в виду всю систему действий по применению аналогии, способствующую полноценному овладению понятием.
Система действий по применению аналогии (метод аналогий)
Опытный исследователь, использующий аналогию в процессе познания какого-либо объекта-оригинала, естественно имеет в виду определённую цель получить какие-то новые сведения об оригинале посредством изучения его моделей. И у него в распоряжении уже имеются, видимо, знакомые ему аналоги оригинала, либо он сам выстраивает нужные ему дополнительные аналоги. Но этого недостаточно, поскольку аналог становится моделью лишь в процессе познания. Так, видимая грамотному математику аналогия между, например, арифметической и геометрической прогрессиями может быть и незамеченной учащимися школы. Но даже если и будет замечено некоторое сходство между ними, всё же сами эти объекты могут восприниматься и изучаться независимо друг от друга, что, впрочем, часто и случается. Чтобы аналог стал действительно моделью изучаемого объекта, его необходимо сделать инструментом познания. Для этого должны быть созданы определённые условия: (а) изучаемый объект и его аналог должны попасть в поле зрения исследователя и (б) он должен «увидеть» аналогию между ними.
Кроме того, исследователь, как правило, сам задаёт объект исследования (оригинал) и намечает, хотя бы приблизительно, тот набор S его характеристик – базу аналогии [6, c. 247], относительно которого будут им подбираться или выстраиваться соответствующие аналоги. Таким образом, исследователь создаёт ещё одно необходимое условие применения аналогии: (в) он на том или ином уровне понимает (возможно, чувствует) аналогию как отношение структурного сходства и как основание для получения с её помощью новых сведений об оригинале. Условия (а) – (в) приобретают особое значение и имеют свою специфику в процессе обучения, когда «исследователями» становятся учащиеся. Тогда эти условия отражают психологическую сторону применения аналогии и должны стать результатом специальных умственных действий учащихся, организованных учителем. В частности, оригинал, цель его учебного исследования, и его модели должны быть приняты учащимися. Это становится возможным в результате выполнения учащимися под руководством учителя следующего комплекса подготовительных учебных действий:
Д′п. Выделение из учебной ситуации оригинала и определение цели его исследования (изучения), принятие их учащимися для себя;
Д′′п. Создание у учащихся сведений о возможных аналогах оригинала хотя бы на уровне представлений об их похожести в чём-то (с чем похожим мы встречались раньше, при изучении такого-то материала?..);
Д′′′п. Создание у учащихся представлений об аналогии между изучаемым и вспомогательными объектами, выявление хотя бы первичной информации о базе аналогии. (В чём эти объекты похожи на наш, в чём их отличие? От каких свойств при изучении основного объекта мы не можем отказаться?..)
Эти действия хотя и относительно самостоятельны, тем не менее, составляют единый комплекс и служат в учебном процессе одной цели – преобразованию начальной учебной ситуации в ситуацию по применению аналогии. Обозначим этот комплекс действий Дп. После достижения (на том или ином уровне) указанной цели наступает очередь комплексу Др – действий реализующих, о некоторых из них уже говорилось выше. В этом комплексе также методически целесообразно выделить отдельные действия, и в качестве одного из первых отметим Д′р: выбор из известных или построение относительно новых возможных моделей данного оригинала. Следующее действие Д′′р состоит в исследовании модели (моделей) для отыскания таких их характеристик, которые могут быть перенесены на оригинал. В процессе выполнения этого действия чаще всего оказываются необходимыми переформулировки или даже переосмысливание выявленных характеристик моделей уже как характеристик оригинала. В общем можно сказать, что мы преобразуем выявленные характеристики моделей в характеристики оригинала – в этом суть ещё одного реализующего действия Д′′′р.
Заметим, что в методической литературе именно последнее из выделенных реализующих действий получило наибольшее освещение (например, в [11, 14]). Однако, давая в целом полезные рекомендации по переходу от характеристик моделей к соответствующим характеристикам оригинала, авторы чаще всего отождествляли выполнение этого действия со всем комплексом действий по применению аналогии. Это намного сужало проблему и оставляло неясными многие её стороны, в том числе и вопрос об ошибках по якобы аналогии (на самом деле, как уже говорилось, из-за неумения ею грамотно пользоваться, что проистекало от её лишь интуитивного понимания). Для подтверждения сказанного и необходимости самостоятельного выполнения действия Д′′′ имеет смысл обратиться к известному из [10, с. 45, 46] примеру задачи о центре тяжести тетраэдра и внимательно проанализировать рекомендации Д.Пойа по завершению использования аналогии. И, конечно же, надо понимать особенности аналогии как основания для получения, вообще говоря, лишь гипотетических выводов об оригинале.
Особенно в связи с отмеченным свойством гипотетичности выводов по аналогии естественно дополнить предыдущие действия группой Дк контролирующих действий, включив их в состав всей совокупности действий по применению аналогии. Чтобы выявить отдельные действия этой группы, обратимся к анализу причин гипотетичности сведений об оригинале, полученных на предыдущих этапах. Эти причины, по меньшей мере, таковы:
1) преобразования характеристик моделей в характеристики оригинала происходит не по законам дедуктивных выводов и уже потому могут носить лишь вероятный характер, характер предположения, пока не доказанного;
2) основание для получения этих выводов, то есть аналогия, используется на предыдущих этапах на допонятийном уровне, то есть, не выявлена и не описана с достаточной степенью точности и полноты;
3) как в процессе познания, так и в обучении аналогия применяется как отношение сходства, как своеобразная эвристика, и потому – в силу особенностей процесса познания чаще всего непроизвольно распространяется за границы её применимости, то есть за рамки логических следствий базы аналогии.
Последняя причина объясняется и свойствами человеческой психики: 1) способностью на незначительном материале создавать обобщающие ассоциации по сходству и 2) закономерностью, обнаруженной П.А. Шеваревым и проявляющейся в снижении степени осознанности отдельных повторяющихся характеристик встречающихся объектов. Так, при изучении понятия степени ас учащиеся склонны забывать, что её основание должно отвечать условию а>0, особенно при с = 1/2k, k ∈ N. Например, в цепочке 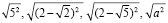 учащиеся, как правило, склонны делать ошибки в последних двух случаях.
учащиеся, как правило, склонны делать ошибки в последних двух случаях.
Чтобы значительно уменьшить число случаев ошибочных выводов при необдуманном применении аналогии, необходимо побудить учащихся выполнить с следующие контролирующие действия:
Д′к. Поиск не только общих (сходственных), но и отличительных характеристик моделей и оригинала. Благодаря этому действию выстраиваются основания для очерчивания границ применимости аналогии;
Д′′к. Проверка истинности сведений, получаемых при выполнении реализующих действий. Благодаря этому действию уточняется и корректируется не только информация об оригинале, но и база аналогии;
Д′′′к. Сравнение сведений о моделях и оригинале как с целью исследования последнего, так и с первоначальной целью исходной учебной ситуации. Результатом этого действие должно стать хотя бы частичное разрешение первоначальной учебной ситуации и, возможно, построение основания для дальнейшего применения аналогии в каких-то изменившихся условиях.
При достижении, хотя бы частичном, цели исходной учебной ситуации и её разрешении иногда возникает возможность повторного применения аналогии в той же или несколько изменённой ситуации. Это одно из первых действий Д′т группы Дт, названной нами [5] группой транслирующих действий (от латинского translation – перенесение). Вполне правомерным является и ещё одно действие этой группы Д′′т – переход к другой учебной ситуации с изменённым объектом исследования, хотя и в чём-то аналогичным оригиналу первой ситуации. Например, решив с учащимися задачу на построение прямоугольного треугольника по гипотенузе и катету, целесообразно на этом же уроке хотя бы поставить задачу на построение, например, произвольного треугольника по двум сторонам и известному углу между ними. Это позволит учащимся увидеть взаимосвязь и аналогию этих задач (и соответствующих понятий) и приобрести обобщённое знание, в том числе – и о группах аналогичных задач или аналогичных изучаемых понятий.
Систему умственных действий Дп – Дт и их материальных воплощений в соответствующей системе учебных заданий назовём методом аналогий в обучении. Эта система действий остаётся неизменной при переходе от одной учебной ситуации к другой, от изучения какого-либо оригинала к другому с применением аналогии, поэтому вполне оправданно можно говорить о методе аналогий как о специфическом методе организации познавательной деятельности учащихся, причём не только при обучении математике. Описанную систему действий можно представить в виде следующей схемы (рисунок).
Приведём далее примеры учебных заданий, которые использовались в нашем опыте изучения степени на основе аналогии и при выполнении которых учащиеся осуществляли контролирующие и транслирующие действия.
Учебные контролирующие и транслирующие задания
Всегда ли выполняются следующие равенства (ответ обоснуйте):
2x + 3x = 5x; c2·c3=– c5; b3·b = b4;
9y – 7y = 2y; a9:a7=–a2; d4:d3 = d; b2:b5 = b3;
5k – 5k = 0; n5: n5 = 1; (3 – a)3 : (3 – a)3 = 12?
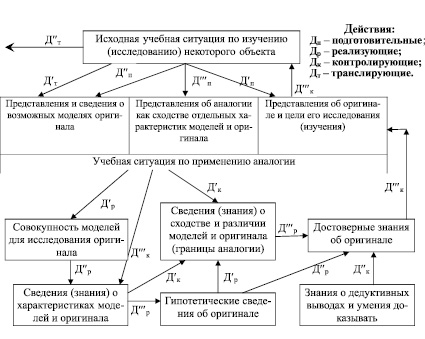
Вместо вопросительного знака поставьте знаки «>», «<», «=» так, чтобы утверждения были истинными (ответ обоснуйте):
32 ? 33 ; 32 ? 30; 3·2 ? 3?0; 23×? 32; 22 ? 2·2; (–4)·1? (–4)1;
5×4 ? 4×5; 54 ? 45; 10 ? 01; (3y – 7y)0 ? (7y – 3у)0;
–5а ? (– а) 5; (1/3)4? (1/4)3; 25 ? 52; (1/5)0 ? (–а)0; (1/b)3? 1/b3.
Найдутся ли такие n (n ∈ N), что будут выполняться равенства: 3n = 3n; 5n = nn ? Ответ объясните. Приведите свои подобные примеры.
Заметим, что аналогия полнее проявляется не столько в сведениях об оригинале, найденных при исследовании моделей, сколько в процедурах перехода от моделей к оригиналу, от исходной ситуации к ситуации применения аналогии и, конечно, в процессе формирования нового понятия на базе известного. Поэтому-то, ещё раз подчеркнём, и необходимы транслирующие действия. В результате их выполнения у учащихся образуются комплексы аналогичных понятий, а сформированные знания и умения становятся более полными и обобщёнными, следовательно, и более устойчивыми. Развиваются способности учащихся по переносу этих знаний и умений в новые ситуации, в целом – способности грамотно и с наименьшим числом ошибок использовать метод аналогии как целостный вид умственной деятельности.
Так, в процессе дальнейшего изучения степени (в 7-м и особенно в старших классах) к транслирующим действиям (и заданиям) целесообразно отнести такие, которые мотивируют учащихся на построение аналогичных последовательностей (множеств) чисел, обозначенных ранее А и В, или даже (в профильных классах, в классах с углублённым изучением математики) расширенных последовательностей А′, В′ (с. 4–5). Приведём задания подобного рода.
Какие числа называют противоположными, какие – взаимно обратными? Приведите примеры. Запишите числа, противоположные и обратные данным, если они существуют; ответ обоснуйте на основе определения:
3; 2; – 5; – а; (-5)2; ј; 0; 1/а; (–4); 30;
7,3; 2×7,3; –3×7,3; –b×7,3; (9а – 7b)×7,3;
(понятно, что 7,3 взято произвольно и в конкретных случаях может быть заменено другим).
Запишите числа в порядке возрастания n (n ∈–2а, 0, а, n× а, –а, – n× а, 2а);
Назовите и запишите числа,, обратные следующим, если такие есть:
4,5; (–5,7)2; 33; –а; 0; 1; а4; аn;
7,3; (7,3)0; (7,3)2; 1/(7,3)3; (7,3)m.
Расположите числа в порядке их возрастания при n ∈ N:
1, 1/b; 1/b2; b2; 1/bn; bm. Как определить взаимно обратные числа?
Как обозначается элемент, противоположный данному, обратный ему?
Завершим данную статью обобщённой моделью учебного и научного познания (рис. 2), которая оказывается полезной для организации обучения математическим знаниям не только в школе, но и в вузе. Она оказалась результатом анализа и обобщения рекомендаций Р. Декарта, А. Эйнштейна и других исследователей по организации процесса познания. Вместе с тем, приведенная выше схема (тоже модель) метода аналогий является конкретизацией обобщённой модели познания на этапах I – III. По времени полученная раньше [6, с. 15], модель метода аналогий оказалась, тем не менее, содержательной в том, что в ней отразилось важное звено обобщённой модели познания: переход от умственного образа (УО) к его материализациям 1 – 6, переходы от одного вида материализации к другим, а от них – к понятию.
Библиографическая ссылка
Жохов А.Л., Юнусова А.А., Юнусов А.А. ПРИМЕНЕНИЕ АНАЛОГИИ В ПРОЦЕССЕ ОБУЧЕНИЯ МАТЕМАТИЧЕСКИМ ПОНЯТИЯМ В ШКОЛЕ // Международный журнал прикладных и фундаментальных исследований. 2017. № 1-2. С. 313-322;URL: https://applied-research.ru/ru/article/view?id=11191 (дата обращения: 07.03.2026).


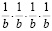 ?
?