Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Кульков В.Г. 1

---

1 Филиал национального исследовательского университета «МЭИ»

Рассматривается строение границ зерен, образующих несоразмерные структуры в атомном масштабе. Основным параметром, позволяющим описывать различные перестройки атомных конфигураций, является дистанция или параметр несоответствия. Внешнее напряжение приводит к появлению конкурирующих состояний атомов с двумя энергетическими ямами. Механизм межкристаллитного проскальзывания состоит в перескоках приграничных атомов между такими состояниями. Для разных типов границ приводятся зависимости скорости проскальзывания от напряжения. Объясняются причины появления различных нелинейностей в таких зависимостях. Исследуется роль примесных атомов в релаксационных процессах на границах зерен. Сдвиговое напряжение приводит к межзеренному проскальзыванию и изменению концентрации атомов примеси на границе. На основе развития модели несоразмерных межкристаллитных границ можно описывать механизмы различных релаксационных процессов. Это такие процессы как миграция границ и зернограничное внутреннее трение.

Статья в формате PDF

1026 KB

межзеренная граница

несоразмерная структура

межзеренное проскальзывание

1. Даринский, Б.М., Муштенко, С.В., Сайко, Д.С. Несоразмерные межкристаллитные границы. 3. Точечные дефекты // Конденсированные среды и межфазные границы. – 2000. – Т. 2, № 4. – С. 333–338.

2. Кульков В.Г. Релаксационные процессы на границах зерен в металлах: монография. – Волжский: Филиал МЭИ в г. Волжском, 2015. – 162 с.

3. Даринский Б.М., Кульков В.Г. Межкристаллитное скольжение вдоль границ, образованных плотноупакованными плоскостями // Поверхность. Физика, химия, механика. – 1993. – № 5. – С. 153–156.

4. Кульков В.Г Кинетика фасетирования несоразмерной межкристаллитной границы наклона // Неорганические материалы. – 2005. – Т. 41, № 7. – С. 892–896.

5. Кульков В.Г Кинетика двумерного фасетирования межкристаллитных границ // Неорганические материалы. – 2005. – Т. 41, № 11. – С. 1405–1408.

6. Кульков В.Г. Межзеренное проскальзывание по границе, сопрягающей плотноупакованную и некристаллографическую плоскости // Вестник МЭИ. – 2005. – № 5. – С. 96–100.

7. Даринский Б.М., Кульков В.Г. Межкристаллитное скольжение вдоль границ, содержащих примеси // Письма в Журнал технической физики. – 1992. – Т. 18, № 2. – С. 65–68.

8. Даринский Б.М., Кульков В.Г., Шаршаков И.М. Влияние межзёренного проскальзывания на концентрацию примеси в границе // Известия АН. Сер. физическая. – 1993. – Т. 57, № 1. – С. 129–130.

9. Кульков В.Г. Межкристаллитное проскальзывание вдоль фасетированных границ зерен // Поверхность. Рентгеновские, синхротронные и нейтронные исследования. – 2005. – № 11. – С. 108–112.

10. Кульков В.Г. Внутреннее трение на границах зерен с нелинейной вязкостью // Металлы. – 2005. – № 4. – С. 69–73.

11. Кульков А.С., Поляков А.С. Атомный механизм миграции несоразмерной границы наклона // Деформация и разрушение материалов. – 2008. – № 11. – С. 42–47.

12. Кульков А.С., Поляков А.С. Миграция несоразмерной межзеренной границы общего типа // Деформация и разрушение материалов. – 2011. – №1. – С. 11–16.

13. Кульков А.С., Поляков А.С. Изменение концентрации вакансий в мигрирующей границе зерна // Металлы. – 2009. –№ 6. – С. 105–109.

Несоразмерными являются такие межкристаллитные границы, в области которых основные геометрические элементы, такие как атомные ряды, плоскости или их следы, образуют несоразмерную структуру. Последнее подразумевает, что отношение расстояний между выбранными характерными элементами сопрягающихся кристаллитов является иррациональным числом. Примером может служить граница наклона в простой кубической решётке с сопряжением плоскостей (100) и (110), так что направление [001] в решетках совпадает. Отношение периодов идентичности между параллельными атомными рядами в границе составляет 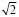. Несоразмерность имеет место в одном направлении в границе. Кроме того, несоразмерные структуры могут возникать в двух или трех измерениях.

Основным параметром, характеризующим атомные конфигурации, здесь является т.н. дистанция (параметр несоответствия) [1], указывающая на взаимное расположение элементарных структурных единиц в ближайших атомных конфигурациях, взятых из разных решеток. Дистанция определяется нерелаксированной структурой сопрягаемых приграничных атомных плоскостей (или областей). Именно такая величина определяет дальнейшие смещения приграничных атомов в процессе релаксации структуры. Ею детально можно описывать все взаимные атомные перестройки, происходящие в границах при различных релаксационных процессах [2].

Целью настоящей работы является описание механизмов такого релаксационного процесса как межкристаллитное проскальзывания под действием приложенных вдоль границы касательных напряжений.

Описание моделей перестройки структуры границ

Рассмотрим границу, образованную контактом плотноупакованных кристаллографических плоскостей соседних зёрен. Для определённости считаем, что граница образована плоскостями (100) ОЦК решетки, взаимно развёрнутыми на неспециальный угол γ вокруг оси, нормальной к границе. Будем считать, что граничные атомы каждой из решёток находятся в потенциальном поле, образованном граничными атомами соседней решётки. Каждый такой рельеф до сопряжения зёрен имеет симметрию плоской квадратной решётки и минимумы в центрах квадратов. Введём одинаковым образом в каждой такой ячейке рельефа систему координат и обозначим через ρ радиус-вектор вдоль границы попадающего в ячейку атома другой решётки прежде, чем ее структура релаксирует. Как сказано выше, эту величину будем называть дистанцией указанного атома. Можно рассматривать одну т.н. приведенную ячейку, в которой распложены точки, соответствующие граничным атомам сопряженной решетки. Характерным для несоразмерных структур является равномерное распределение дистанций по площади приведенной ячейки. Атомы, попадая в область внутри ячейки, будут смещаться под действием сил взаимодействия с атомами своей решётки и потенциального поля ячейки. При этом для атомов с дистанциями, близкими к границам ячейки, будут наблюдаться двухъямные энергетические конфигурации с более глубокой ямой в своей ячейке и менее глубокой в соседней [2].

Сдвиговое напряжение σ, действующее в плоскости границы, приводит к тому, что часть атомов будет перескакивать из своих ям в соседние. Условием перескока атомов является уменьшение их энергии после скачка .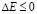

Обозначим через 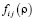функцию распределения атомов по ямам, численно равную вероятности того, что атом находится в своей яме, то есть, перескок еще не произошёл. Можно рассматривать 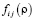отдельно для каждой из четырёх ориентаций границ квадратных ячеек (по две на каждую решётку). Полагая в стационарном режиме скольжения 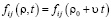и вводя для каждой стороны ячейки координаты x и 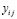так, что ось x направлена вдоль скорости u, а 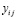– вдоль стороны соответствующей ячейки, запишем релаксационное уравнение

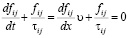, (1)

где τiij – время релаксации.

На основе решения этого уравнения [3] можно получить выражение для величины скорости проскальзывания

,

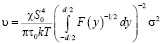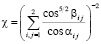. (2)

Здесь S0 – площадь одной ячейки, d – ее сторона, τ0 – период колебаний атомов, F – функция, определяющая вероятность перескоков атомов в зависимости от их положения в ячейке, αij и βij – углы между направлениями напряжения, скорости и сторонами ячеек, kT – фактор Больцмана. Направление проскальзывания в общем случае произвольной разориентации кристаллитов и направления действия сдвигающей силы не совпадает с последним.

Довольно распространенным типом межзеренных границ, имеющих отношение к обсуждаемому виду, являются границы, образованные сопряжением плотноупакованной кристаллографической плоскости с атомно рыхлой поверхностью некристаллографического типа. Участки такого рода границ могут образоваться в процессе фасетирования высокоугловой границы общего типа [4, 5], поскольку стремление к плотной упаковке атомов на граничной поверхности кристаллита понижает полную энергию границы. Некристаллографические плоскости имеют среди индексов Миллера один или два иррациональных индекса, что и является причиной образования несоразмерной структуры. Можно считать, что атомы рыхлой поверхности находятся в потенциальном рельефе плотноупакованной поверхности. Смещение кристаллита приводит к попаданию атомов за пределы этой поверхности в область повышенной энергии. Подстройка структуры происходит путем диффузионного удаления таких атомов в различного рода стоки. Учитывая наличие значительного свободного объема в границе, можно принять, что главными стоками являются структурные граничные вакансии. Вводится понятие приведенного источника подобно тому, как вводилась выше приведенная ячейка. Диффузионная задача может рассматриваться с точки зрения вакансий, их источников и стоков. Решая двумерную диффузионную задачу 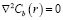с граничными условиями, выражающими связь избыточной по сравнению с равновесной концентрации вакансий 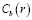в границе с изменением локального значения химического потенциала

,

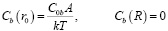находим поток из источника

.

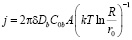Здесь Db – зернограничный коэффициент диффузии вакансий, δ – диффузионная ширина границы, 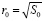– размер приведенной ячейки, 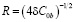– среднее расстояние в границе между источниками и стоками; C0b – равновесная концентрация вакансий в границе, A – работа, совершенная внешним напряжением в расчетcе на один переместившийся атом. На основе решения диффузионной задачи поолучаем выражение для скорости проскальзывания [6]:

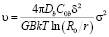. (3)

Здесь G – эффективный модуль сдвига границы, а коэффициент B определяет связь скорости с количеством мигрирующих атомов в единицу времени.

Интересен один частный случай строения границы, когда она образована контактом поверхностей с параллельными плотноупакованными атомными рядами, так что только один из индексов Миллера рыхлой поверхности является иррациональным. В этом случае источники вакансий в границе являются линейными, а диффузионная задача – одномерной. Проводя аналогичные рассуждения, можно получить выражение для скорости проскальзывания в этом случае:

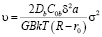, (4)

где 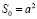. Число диффундирующих атомов пропорционально напряжению, однако в случае достаточно больших величин напряжения это число перестает зависеть от него. Достигается режим насыщения по числу активных атомов [6], что приводит к линейной связи скорости проскальзывания с напряжением.

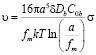. (5)

Менее рыхлая граница имеет меньшее количество структурных вакансий. В этом случае стоками атомов являются индуцированные стоки с пониженной атомной плотностью, создающиеся упругим смещением одного зерна относительно другого. Для двумерной диффузии атомов в границе вместо (3) получаем 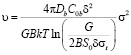[6]:

, (6)

а для границы с параллельными атомными рядами

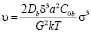. (7)

Величина, обратная показателю степени при напряжении, называется показателем скоростной чувствительности. Его значения зависят от типа границ и степени их чистоты.

Влияние примесей на процессы пластической деформации в поликристаллических материалах может быть весьма значительным. Модель проскальзывания по межзёренным границам, развитая выше, позволяет провести количественное рассмотрение вопроса [7]. Вернемся к рассмотрению границ, образованных сопряжением плотноупакованных плоскостей. Примесные атомы располагаются в случайно образованных пустотах границы достаточных размеров. Атом примеси, попадая в некоторую яму, исключает возможность попадания в неё другого атома, т. е. числа заполнения ям принимают значения 0 и 1. В этих условиях для вероятности заполнения ям справедливо выражение Ферми-Дирака:

.

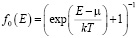где E – энергия атома в яме; μ – химический потенциал примеси.

По мере проскальзывания атомы примеси, находящиеся в ямах, превращаются в своеобразные стопоры, препятствующие смещению зёрен в местах их расположения. По истечении некоторого времени τ атом примеси покидает яму, диффузионно удаляясь на некоторое расстояние вдоль границы и устраняя тем самым существовавший стопор. Характер проскальзывания будет определяться соотношением между временем диффузионного перемещения примесных атомов и временем перескоков через барьеры собственных приграничных атомов зёрен. Если первая величина намного меньше второй, то процесс проскальзывания будет происходить аналогично рассмотренному в начале. При этом атомы примеси практически не будут оказывать влияния на величину скорости. В противоположном случае атомы основного вещества будут перескакивать быстрее, так что можно считать, что скорость проскальзывания определяется диффузионными характеристиками атомов примеси.

Детальное рассмотрение вопроса [7] приводит к выражению

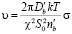. (8)

Здесь 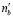определяется как количество атомов примеси на единице площади границы, 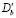– коэффициент примесной граничной диффузии, χ – коэффициент зависимости энергии примесного атома от дистанции.

Наличие напряжения на границе приводит к упругому сдвигу зерен, на который накладывается процесс проскальзывания. Энергия примесных атомов при этом повышается, и они частично уходят в объем [8]. Концентрация примеси на границе уменьшается по экспоненциальному закону

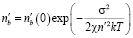. (9)

Учитывая (8), можно считать, что зависимость от скорости имеет аналогичный вид с другим коэффициентом в экспоненте.

Рассмотренные в настоящей работе механизмы проскальзывания относятся к плоской границе в мезоскопическом масштабе. Большинство же реальных границ зерен в поликристаллах не является таковой, а состоят из сегментов с различной ориентацией. Примером может служить класс т.н. фасетированных границ. Эти границы неизбежно имеют нормальные компоненты напряжений. Поэтому механизм проскальзывания по ним имеет диффузионную природу [9] и связан с перераспределением вещества между различно ориентированными фасетками.

Заключение

В рассматриваемых случаях чистых границ контролирующий механизм скольжения заключается в локальном повышении энергии конфигураций из отдельных атомов или их рядов и последующей их диффузионной релаксации. В области малых внешних напряжений 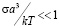число таких конфигураций и их энергия пропорциональны величине напряжения. Скорость же скольжения пропорциональна произведению этих величин, что приводит к параболической зависимости ее от напряжения в выражениях (2)–(4), (6). В области напряжений с насыщением количества мигрирующих атомов или в примесных границах один из факторов отпадает, поэтому зависимость скорости от напряжения становится линейной согласно (5) и (8). Другие зависимости могут быть связаны с иной геометрией диффузионного поля атомов или вакансий, как это имеет место в (7). Любые нелинейности зависимости 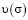проявляются в отличии параметров пика внутреннего трения от дебаевского [10], поскольку основным механизмом зернограничного внутреннего трения является межкристаллитное скольжение.

Развитие несоразмерной модели строения межкристаллитных границ оказалась весьма плодотворной для описания и других зернограничных релаксационных процессов, например, миграции границ [11–13].

Библиографическая ссылка