В настоящее время одним из самых перспективных направлений развития систем передачи информации считается метод мультиплексирования с ортогональным частотным разделением каналов (OFDM-Orthogonal Frequency Division Multiplexing). Однако, для представления переменных и выполнения арифметических операций в системах OFDM, реализуемых с использованием преобразования Фурье и его быстрых модификаций (FFT – Fast Fourier Transform, IFFT-Inverse Fast Fourier Transform) используется конечное число битов. Более того, реализация FFT характеризуется наличием двух вычислительных трактов и предопределяет значительные погрешности при вычислении значений спектральных коэффициентов в поле комплексных чисел, обусловленные тем, что поворачивающие коэффициенты представляют собой иррациональные числа [3, 4]. Указанные особенности реализации FFT над полем комплексных чисел приводят к снижению показателей системы OFDM.
Цель исследования. Добиться качественных изменений систем OFDM можно за счет использования ортогональных преобразований, определенных на алгебраических системах обладающих структурой кольца или поля, в том числе и конечных (конечное кольцо вычетов по модулю целого числа, конечное поле Галуа) [2, 3]. При этом возможно не только повысить точность и скорость обработки сигналов, но и обеспечить отказоустойчивость вычислительного устройства OFDM. Реализация арифметических операций конечного поля или кольца значительно проще по сравнению с реализацией поля комплексных чисел, поскольку элементы поля Галуа или кольца вычетов обычно кодируются целыми числами. Операции сложения и умножения в этих системах представляют собой сложение и умножение по модулю целого числа, практически операции производятся над целыми, а не комплексными числами.
Целью работы является повышение эффективности OFDM за счет использования ортогональных преобразований над конечным полем или кольцом за счет точности вычислений.
Материалы и методы исследования
В основе реализации OFDM лежит способ синтеза сложного сигнала из отдельных гармонических составляющих на основе обратного преобразования Фурье. Синтетическим методом создается спектр сигнала, из которого с использованием IFFT получается аналоговый сигнал. Спектр такого сигнала уже состоит из ортогональных поднесущих по определению преобразования Фурье.
Синтез OFDM сигнала предусматривает использование ряда ортогональных поднесущих, 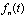 модулированных комплексными информационными символами
модулированных комплексными информационными символами 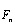 . Ортогональность обеспечивается на так называемом полезном интервале времени Tu при выполнении условия:
. Ортогональность обеспечивается на так называемом полезном интервале времени Tu при выполнении условия:
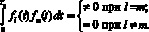 (1)
(1)
Комплексный информационный модулирующий символ имеет вид:
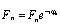 , (2)
, (2)
где Fn – амплитуда символа, 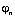 – фаза символа,
– фаза символа, 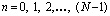 .
.
Задача, решаемая OFDM, сводится к получению на временном интервале Tu непрерывного сигнала, состоящего из N ортогональных поднесущих, 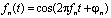 , модулированных символами
, модулированных символами 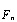 :
:
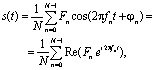 (3)
(3)
где fn – частота n-й поднесущей.
Из (1) и (3) следует, что ортогональность модулированных поднесущих обеспечивается при выполнении условия:
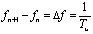 , (4)
, (4)
где 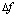 – разнос между соседними поднесущими.
– разнос между соседними поднесущими.
Выберем период дискретизации T из условия:
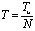 , (5)
, (5)
и проведем преобразование выражения (3), перейдя от непрерывного времени к дискретному:
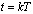 , (6)
, (6)
где 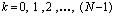 .
.
В результате получим значения дискретизированного по времени сигнала:
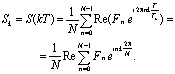 (7)
(7)
Таким образом, мы перешли от непрерывной формы описания OFDM сигнала (3) к дискретной (7). Полученное выражение представляет собой действительную часть обратного дискретного преобразования Фурье (DFT – Discrete Fourier Transform, IDFT – Inverse Discrete Fourier Transform). IDFT в OFDM системах осуществляется в комплексной форме, поэтому выражение (7) представим в виде:
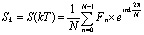 . (8)
. (8)
Выражение (8) отражает процесс модуляции поднесущих информационными символами 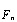 и определяет значение OFDM сигнала в моменты времени kT:
и определяет значение OFDM сигнала в моменты времени kT:
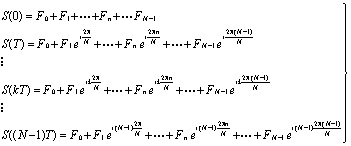 (9)
(9)
Анализ полученной системы позволяет выделить три момента:
1. процесс формирования поднесущих и их модуляция в рамках OFDM совмещены;
2. каждый символ модулирует только одну поднесущую;
3. в формировании каждого отсчета принимают участие все символы.
Процесс демодуляции OFDM сигнала основан на применении прямого дискретного преобразования Фурье DFT к сформированным на основе принятого сигнала временным отсчетам S(kT):
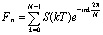 . (10)
. (10)
Раскрыв выражение (9) получим систему из N уравнений, определяющих комплексные значения информационных символов 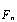 :
:
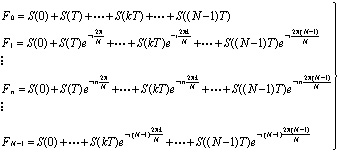 (11)
(11)
Из полученной системы следует, что выделение символов 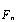 реализуется суммированием на интервале Tu произведений значений OFDM сигнала на определенные экспоненты и возможно благодаря ортогональности системы, включающей комплексные экспоненты и функции, описывающие поднесущие.
реализуется суммированием на интервале Tu произведений значений OFDM сигнала на определенные экспоненты и возможно благодаря ортогональности системы, включающей комплексные экспоненты и функции, описывающие поднесущие.
Оценим величины ошибок, возникающих при OFDM модуляции и демодуляции по формулам (9) и (11) при использовании арифметических устройств с фиксированной запятой.
Для эффективного расчета комплексных коэффициентов DFT и IDFT, входящих в (9) и (11) на практике используется FFT и IFFT [11]. Основной операцией в FFT, IFFT является «бабочка», которая описывается следующими уравнениями:
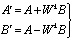 , (12)
, (12)
где А и В – входы «бабочки», 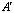 и
и 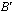 – ее выходы. Настроечный параметр
– ее выходы. Настроечный параметр 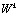 , а также входы и выходы – комплексные. В реализации с фиксированной запятой вычисление «бабочки» выполняется с использованием действительной арифметики, поэтому
, а также входы и выходы – комплексные. В реализации с фиксированной запятой вычисление «бабочки» выполняется с использованием действительной арифметики, поэтому 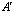 и
и 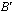 можно выразить в виде:
можно выразить в виде:
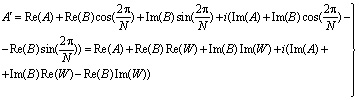 (13)
(13)
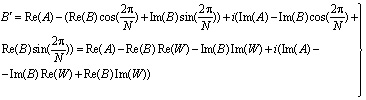 (14)
(14)
Из (13) и (14) следует, что вычисление по схеме "бабочка" требует четырех умножений и пяти действительных сложений. В реализации с фиксированной запятой каждое произведение в (13) и (14) требует для представления приблизительно вдвое большего числа битов, чем требуется для записи одного операнда по отдельности. Например, если переменные 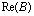 ,
, 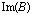 ,
, 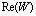 и
и 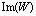 представлены как 16 – битовые числа, то после умножения представление каждого произведения потребует 32 бит. Усечение или округление каждого произведения до прежних 16 бит порождает ошибку округления.
представлены как 16 – битовые числа, то после умножения представление каждого произведения потребует 32 бит. Усечение или округление каждого произведения до прежних 16 бит порождает ошибку округления.
Таким образом, с каждой «бабочкой» можно связать четыре источника шума округления, по одному для каждого произведения. При этом, шум порождаемой “бабочкой” на каждом этапе, поступает на следующие этапы. В [1] показано, что в предположении о порождении всеми «бабочками» идентичных, но некоррелирующих ошибок, максимальная мощность шума (дисперсия) в каждом выходе FFT, IFFT равна:
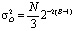 , (15)
, (15)
где B – длина слова системы в битах, N – размер FFT, IFFT.
Кроме этого, после сложения по формулам (13) и (14) возникают ошибки переполнения за счет роста размера данных после расчета каждой «бабочки». Для борьбы с ошибками переполнения используется механизм масштабирования. Одна из наиболее популярных схем масштабирования основана на наблюдении, что максимальный модуль выхода каждой «бабочки» увеличивается от этапа к этапу в два раза [1]:
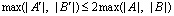 . (16)
. (16)
Из (16) следует, если входы «бабочки» умножить на коэффициент 0,5 в выходах не должно возникнуть переполнения, при условии, что амплитуда входных данных принадлежит диапазону разрешенных длин слов. Однако заметим, что в некоторых случаях, масштабирования с коэффициентом 0,5 недостаточно для предотвращения переполнения, даже если вход меньше единицы.
Результаты исследования и их обсуждение
Пусть 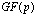 – конечное поле Галуа, GN – циклическая группа порядка N,
– конечное поле Галуа, GN – циклическая группа порядка N, 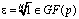 . Преобразованием Фурье-Галуа (ПФГ, ОПФГ-обратное преобразование Фурье-Галуа) будем называть преобразования сигнала
. Преобразованием Фурье-Галуа (ПФГ, ОПФГ-обратное преобразование Фурье-Галуа) будем называть преобразования сигнала 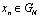 вида:
вида:
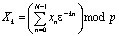 ,
,
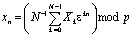 . (17)
. (17)
Аналогичные преобразования, определенные над конечным кольцом вычетов называют теоретико-числовыми преобразованиями (ТЧП).
ПФГ и ТЧП по своей структуре наилучшим образом реализуются с использованием цифровой элементной базы. Например, если взять ε в виде степени двойки, то умножение в (10) на степени 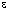 при вычислении ПФГ, ТЧП заменяются сдвигами кодовых слов и приведением сдвинутых кодовых слов по модулю простого числа p.
при вычислении ПФГ, ТЧП заменяются сдвигами кодовых слов и приведением сдвинутых кодовых слов по модулю простого числа p.
С учетом (17) ПФГ, ТЧП модуляция поднесущих информационными символами Fn в моменты времени kT приобретает вид, аналогичный (9):
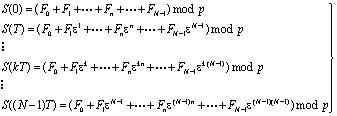 (18)
(18)
Процесс демодуляции ПФГ, ТЧП OFDM сигнала осуществляется прямым ПФГ, ТЧП к сформированным на основе принятого сигнала временным отсчетам S(kT):
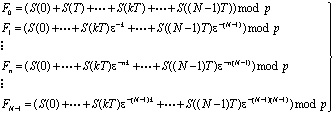 (19)
(19)
Выбор значений p, ε, N целесообразно осуществлять под конкретную реализацию OFDM. В плане аппаратурной реализации, математические модели, определенные над конечными полями или кольцами, не являются альтернативой классическим моделям и могут быть реализованы с помощью обычных цифровых вычислительных машин (ЦВМ), ориентированных на решение задач цифровой обработки сигналов. Однако, реализация моделей будет более эффективной, если в ЦВМ арифметические операции конечных полей или колец (модульные операции) реализуются не программным, а аппаратурным путем. Для этого нет необходимости снабжать ЦВМ еще одним арифметическим устройством. Потребуется только расширение функциональных возможностей имеющегося арифметического устройства за счет модульных операций, так как обычные арифметические операции и модульные можно совместить при реализации в одном устройстве [3].
Заключение
Производительность систем OFDM, реализуемых с использованием преобразования Фурье и его быстрых модификаций ограничена числом битов, используемых в ее реализации. Основными источниками ошибок являются:
– округление произведений при вычислении «бабочки» по формулам (13) и (14), при этом, мощность возникающего шума прямо пропорциональна размеру FFT, IFFT;
– переполнение при сложениях по формулам (13) и (14), более того, в некоторых случаях, масштабирование данных не предотвращает ошибок переполнения.
В работе показана возможность и целесообразность использования ортогональных преобразований, определенных на алгебраических системах обладающих структурой конечного кольца или поля для систем связи с OFDM. Применение указанных преобразований позволит повысить производительность систем с OFDM за счет отсутствия ошибок округления произведений и переполнений при вычислениях по формулам (18) и (19) или «бабочки» в конечных кольцах или полях.
Библиографическая ссылка
Юрданов Д.В., Калмыков М.И., Журавлев К.М., Калмыков И.А. ИСПОЛЬЗОВАНИЕ ТЕОРЕТИКО-ЧИСЛОВЫХ ПРЕОБРАЗОВАНИЙ ДЛЯ СИСТЕМ СВЯЗИ С OFDM // Международный журнал прикладных и фундаментальных исследований. 2017. № 3-2. С. 178-182;URL: https://applied-research.ru/ru/article/view?id=11421 (дата обращения: 02.03.2026).

