Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Киреева Н.В. 1 Чупахина Л.Р. 1 Караулова О.А. 1

---

1 ФГБОУ ВО «Поволжский государственный университет телекоммуникаций и информатики»

Исследован multicast трафик, обладающий признаками самоподобия. По результатам измерения сетевого трафика рассмотрены вероятности интенсивности видеотрафика, которые описываются распределениями с «тяжелым хвостом» – Вейбулла и Парето. Данные распределения позволяют описать снятый трафик и аппроксимировать функции распределений интервалов времени между пакетами и длительности обслуживания суммой затухающих экспонент. Параметры, полученные при рассмотренной аппроксимации, используются для решения интегрального уравнения Линдли спектральным методом.

Статья в формате PDF

1780 KB

анализ трафика сети

распределение Вейбулла

распределение Парето

самоподобие

видеоконференция

качество обслуживания

1. Исследование характеристик видеотрафика мультисервисной сети / О.А. Караулова // Сборник докладов 71-й Международной конференции «Радиоэлектронные устройства и системы для инфокоммуникационных технологий». – Т. 2, 2016. – С. 320 – 321.

2. Карташевский В.Г. Основы теории массового обслуживания / В.Г. Карташевский. – М.: Радио и связь, 2006. – 107 с.

3. Клейнрок Л. Теория массового обслуживания. – М.: Машиностроение, 1979. – 432 с.

4. Метод аппроксимации произвольной плотности распределения суммами экспонент / И.А. Блатов, В.Г. Карташевский, Н.В. Киреева // Вестник ВГУ. – 2013. – № 2. – С. 53–57.

В современных условиях видеотрафик является наиболее приоритетным, так как все современные технологии поддерживают данный тип трафика. Этот тип трафика высокочувствителен и критичен к задержкам. В связи с этим очень важно спрогнозировать средние характеристики качества облуживания (QoS). Одним из более актуальных видеотрафиков является трафик видеоконференций, который требует большую пропускную способность и минимизацию времени доставки видеокадров до получателя. Для проведения видеоконференций используется трафик реального времени, который предоставляет мультимедийные сервисы передачи информации между пользователями в реальном масштабе времени. Передача видеоконференции предъявляет высокие требования к параметрам качества обслуживания, а именно к задержкам, джиттеру, потерям пакетов, пропускной способности и др. Для достижения оптимальных значений качества обслуживания используются разные принципы передачи трафика реального времени (unicast, multicast).

В работе [1] были исследованы характеристики разных типов видеотрафика. Регистрация трафика велась по схеме, изображенной на рис. 1. В данной работе рассматривается аппроксимация видеотрафика с помощью уравнения Линдли для multicast трафика.

В результате проведенного исследования [1] была получена реализация зарегистрированного multicast трафика с помощью Wireshark, представленная на рис. 2.

Данный трафик характеризуется сильной неравномерностью интенсивности поступления пакетов. Пакеты не плавно рассосредоточены по разным интервалам времени, а группируются в одних интервалах или рассредоточены в иных интервалах времени.

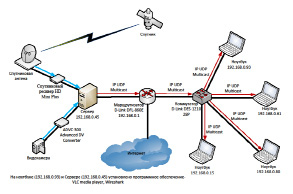
Рис. 1. Регистрация видеоданных, метод передачи – multicast

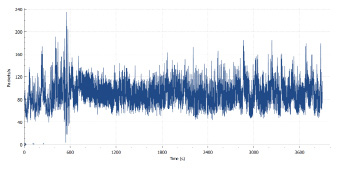
Рис. 2. Реализация multicast видеотрафика

Исходя из полученной реализации видеотрафика, изображенной на рис. 2, можно сделать вывод о том, что данный трафик обладает свойствами самоподобия. С помощью ПО Fractan была определена степень самоподобия и определен параметр Херста, который составил H=0,5249. Данный результат говорит о наличие свойств самоподобия исследуемого multicast видеотрафика.

Самоподобный характер multicast видеотрафика затрудняет аналитические расчеты показателей качества функционирования с помощью классических методик теории массового обслуживания, поэтому актуальнее применять аппроксимации реальных функций плотностей вероятностей интервалов времени между пакетами и длин пакетов.

Проведено исследование вероятностей интенсивности multicast видеотрафика. С помощью ПО EasyFit построены гистограммы распределений случайных величин интенсивности. Для полученных гистограмм по критериям согласия Колмогорова-Смирнова, подобраны аппроксимирующие распределения из библиотеки EasyFit. На рис. 3 изображено распределение случайных интервалов времени между пакетами, а на рис. 4 распределение длин пакетов входного трафика.

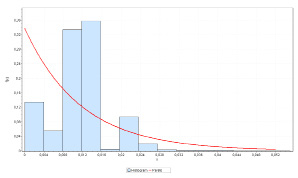
Рис. 3. Распределение Pareto – распределение случайных интервалов между пакетами

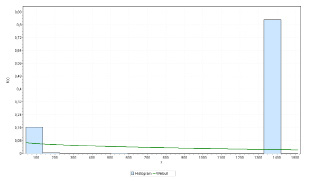
Рис. 4. Распределение Weibull – распределение длин пакетов входного трафика

Как было сказано выше, анализ характеристик видеотрафика multicast проведен с использованием интегрального уравнения (ИУ) Линдли [2].

Исследование метода расчета ИУ Линдли производится по спектральному методу, где неизвестную функцию плотности распределения времени ожидания можно найти, решая данное уравнение и представляя входные функции распределений в виде суммы затухающих экспонент.

Уравнение Линдли имеет следующий вид [3]:

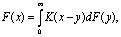
где F – функция распределения времени ожидания требования в очереди; K – ядро, связывающее произвольную функцию распределения вероятностей интервалов времени между поступлениями соседних требований A(t) и произвольную функцию распределения длительности обслуживания требований B(t).

Суть классического (спектрального) метода [3] решения уравнения Линдли заключается в следующем.

Необходимо для выражения

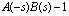
найти подходящее представление в виде:

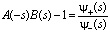, (1)

где A(s) и B(s) – преобразование Лапласа плотности распределения промежутков времени между поступлениями пакетов и плотности распределения времени обслуживания, соответственно.

Поэтому после получения гистограмм и определения параметров функций (Парето и Вейбулла) производим аппроксимацию в виде сумму затухающих экспонент. Метод решения ИУ Линдли можно применить, если для плотностей вероятности a(t) и b(t), соответствующих распределениям A(t) и B(t), использовать аппроксимацию в виде суммы затухающих экспонент [4]

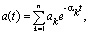
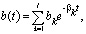
Согласно методу, изложенному выше для a(t) – распределения Парето с параметрами 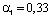, , 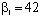можно предложить аппроксимацию в виде:

,

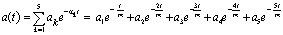где 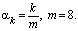Абсолютная погрешность аппроксимации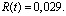

Аналогично для 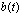 – распределения Вейбулла с параметрами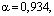 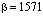аппроксимация в виде суммы затухающих экспонент:

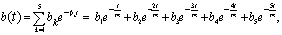
где 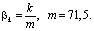Абсолютная погрешность аппроксимации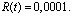

В результате для системы P/W/1 с данными параметрами распределения функция распределения времени ожидания F(x) имеет следующий вид (рис. 5)

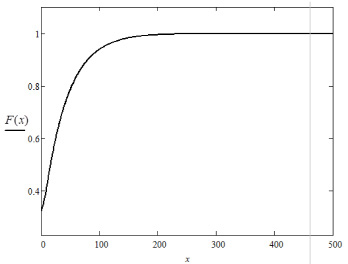
Рис. 5. График функции распределения времени ожидания F(x)

Значение функции распределения времени ожидания F(x) в нулевой точке определяет вероятность отсутствия очереди, то есть новое требование не стоит в очереди.

Соответственно, согласно [3] было определено среднее время ожидания пакета в очереди tср= 29,46 в выбранных ед. вр.

Выводы

В современных условиях применения видеотрафика является наиболее приоритетным, и в силу того, что в основном используются такие приложения как интерактивные видеоконференции, видео по запросу и потоковое видео в реальном времени. Требования к QoS для различного рода трафика отличается, однако существует ряд критичных характеристик (задержки, джиттер, потеря пакетов). Поэтому рассмотрение прогнозирования поведения реального видеотрафика в передающей среде остается открытым и актуальным вопросом. В данной работе показано, что наличие самоподобия в данном трафике затрудняет применять известные на данный момент способы проверки и моделирования.

Проведенное исследование с применением спектрального метода решения ИУ Линдли позволяет определить функции распределения времени ожидания и среднее время ожидания пакета в очереди.

Библиографическая ссылка