Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Нурмаганбетова М.О. 1 Нурмагамбетов Д.Е. 2 Мырзакеримова А.Б. 3

---

1 Казахский национальный медицинский университет им. С.Д. Асфендиярова

2 «Партнеры Международного образования»

3 Международный университет информационных технологии

Разработана на основе математического метода проекции градиентов модель диагностирования. Такой подход обеспечивает более объективное принятие решений. С помощью модели найдено наиболее вероятное заболевание. Данный подход позволил учесть не только степень принадлежности симптомов заболеваниям, но и степень выраженности их. Модель используется для решения задач по принятию решений при нечеткой исходной информации. Математические модели диагностирования, исключающие субъективизм, позволят проводить мониторинги по тем или иным заболеваниям.

Статья в формате PDF

1701 KB

математические методы

модель диагностирования

принятие решений

1. Нурмаганбетова М.О., Нурмагамбетов Д.Е., Оспан А.Б. Влияние степени выраженности симптомов на исходы принятия решения // Международный журнал экспериментального образования. – 2016. – № 4(часть 2) – С. 298-301.

2. Нурмаганбетова М.О., Нурмагамбетов Д.Е., Оспан А.Б. Диагностирование на основе математического метода // Международный журнал экспериментального образования. – 2016. – № 4(часть 2) – С. 298-301.

3. Нурмаганбетова М.О. Математические подходы в медицинских исследованиях: монография. – Германия, Lambert Akademic-Publishing, 2012, с. 172.

Математический подход к медицинским исследованиям, в частности, к диагностированию заболеваний, является актуальным направлением. Создание моделей, на основе достижений в области математики, для изучения и выяснении фундаментальных принципов организации изучаемых систем, перспективная задача. В медицине, при диагностировании заболеваний идет обработка информации в логической последовательности, называемыми диагностическими алгоритмами, в основе которых лежат детерминированная логика, метод фазового интервала, информационно-вероятностная логика и др., адекватные врачебной логике. Разрабатываемые [1, 2] математические модели диагностирования показывают перспективность такого подхода. Для этих целей применяются диагностические таблицы, встречающиеся в здравоохранении, представляющиеся собой формализованную базу данных по заболеваниям, относящиеся к одному нозологическому классу.

Разработана математическая модель диагностирования заболеваний: инфаркт миокарда, перитонит, крупозная пневмония и тромбоэмболия легочной артерии на основе метода проекции градиентов. Диагностическая таблица [3] основывается на статистических данных, взятых из практического здравоохранения.

Матрица полезностей для заболеваний инфаркт миокарда, перитонит, крупозная пневмония и тромбоэмболия легочной артерии:

где A1 – инфаркт миокарда, А2 – перитонит, А3 – крупозная пневмония, А4 – тромбоэмболия легочной артерии, а состояние системы определяется Xj, J = 1,n и соответственно означает: боли в грудной клетке; боли в животе; повышение температуры; понижение температуры; лейкоцитоз; нарушение сердечного ритма; повышение артериального давления; снижение артериального движения; шум трения перикарда; изменение кардиограммы; бледность кожи; общая заторможенность и т.д.

Пусть у пациента наблюдается боли в животе, артериальное давление снижена, наблюдается общая заторможенность, брюшная полость напряжена, имеется вздутие живота. Тогда:

Состояние пациента запишем следующим множеством:

X~={0.5/X2, 0.7/X8, 0.4/X12, 0.8/X15, 0.6/X17},

где значения: 0.5; 0.7; 0.4; 0.8; 0.6 – степень выраженности симптомов, которые задаются, а нечеткие полезности альтернатив при данном состоянии взяты из матрицы, выше представленного. Состояние пациента представим в виде следующей матрицы А:

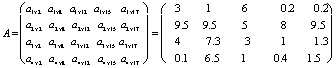
и

Вектор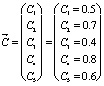

Найдем:

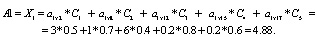
Аналогично:

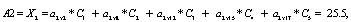
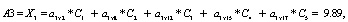
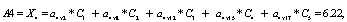
Итак, максимум среди значений: 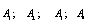будет соответствовать искомому заболеванию, то есть приведенные расчеты позволяют нам поставить диагноз (на основе экспертных оценок): при данном состоянии у пациента наблюдается заболевание А2 (перитонит).

Отсюда множество: (μ(Aio)) = max (4.88; 25.5; 9.89; 6.22).

Поскольку: A(*) = μ ~ (A2o) = 25.5, то оптимальной альтернативой является заболевание A2. Итак, диагноз: наблюдается заболевание перитонит с учетом наблюдаемого у пациента симптомокомплекса и заданного состояния системы (степени выраженности симптомов).

Диагноз, полученный вероятностно-статистическим методом для данных заболеваний и заданного симптомокомплекса, в основе которого лежит формула Байеса, совпал. Данные для вычисления условных вероятностей симптомокомплекса (P(Ski/Bj)) для перечисленных заболеваний, взяты из той же таблицы:

P(Bj/Ski) =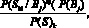

где P(Sk) = .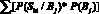

Следует отметить, что этот метод (метод Байеса) имеет ограничение, не учитывает степень выраженности симптомов. Совпадение диагнозов свидетельствует о корректности полученных результатов. Разработанная авторами математическая модель диагностирования заболеваний методом проекции градиентов универсальна, учитывает не только степень принадлежности (полезности μ(Xk)) симптомов заболеваниям, но и степень выраженности симптомов, что позволяет использовать его для прогнозирования заболеваний, поскольку степень выраженности меняется со временем. Возможность реализовать модель технически на ЭВМ, путем создания соответствующей программной системы, исключает субъективизм, который неизбежен при использовании человеческих ресурсов, повысит объективность и достоверность. Автоматизированные системы диагностирования позволят проводить мониторинг по тем или иным заболеваниям. Перспективность данной области исследования не вызывает сомнении.

Библиографическая ссылка