В современной теории дифференциальных уравнений с частными производными теория локальных и нелокальных краевых задач для уравнений смешанного типа является одним из важнейших разделов, изучению которого посвящено немало публикаций. Это объясняется как теоретической значимостью получаемых результатов, так и приложениями в газовой динамике, теории бесконечно малых изгибаний поверхностей, в безмоментной теории оболочек в магнитной гидродинамике, в теории электронного рассеивания, в математической биологии. Важным этапом в теории краевых задач стали нелокальные задачи нового типа, названные задачами со смещением [7]. Они являются обобщением задачи Трикоми, содержат широкий класс корректных самосопряженных задач и имеют многомерные аналоги [1,4]. Эти задачи вызвали интерес многих авторов и были посвящены краевым задачам для уравнений различных типов с классическими операторами и операторами дробного в смысле Римана – Лиувилля дифференцирования в краевых условиях [1–5, 7–9]. Естественным обобщением этой теории явились внутреннекраевые задачи для уравнений смешанного типа. В данной работе исследуется внутреннекраевая задача для уравнения Геллерстедта.
Постановка задачи. Рассмотрим уравнение Геллерстедта
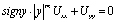 , (1)
, (1)
где 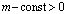 , в конечной области Ω, ограниченной жордановой кривой σ с концами в точках A(0,0), B(1,0), расположенной в полуплоскости
, в конечной области Ω, ограниченной жордановой кривой σ с концами в точках A(0,0), B(1,0), расположенной в полуплоскости 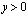 и характеристиками AC, BC уравнения (1), выходящими из точки
и характеристиками AC, BC уравнения (1), выходящими из точки
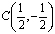 .
.
Пусть Ω1 и Ω2 – эллиптическая и гиперболическая части смешанной области Ω.
Задача. Найти регулярное в области Ω решение U(x,y) уравнения (1), удовлетворяющее условиям
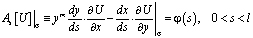 (2)
(2)
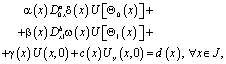 (3)
(3)
где a,b – вещественные числа, S – длина кривой σ, отсчитываемая от точки B; 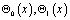 – точки пересечения характеристик уравнения (1), выходящих из точки
– точки пересечения характеристик уравнения (1), выходящих из точки 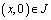 с характеристиками AC, BC соответственно;
с характеристиками AC, BC соответственно; 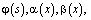
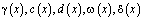 – заданные непрерывные функции, причем
– заданные непрерывные функции, причем
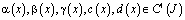 ,
,
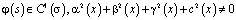 .
.
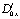 ,
, 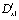 – операторы дробного в смысле Римана–Лиувилля интегро-дифференцирования [10].
– операторы дробного в смысле Римана–Лиувилля интегро-дифференцирования [10].
Доказательство единственности решения задачи. Теорема. В области Ω не может существовать более одного решения задачи (1)–(3), если либо
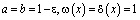 (4)
(4)
и выполняются условия
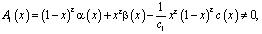 (5)
(5)
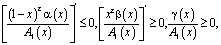 (6)
(6)
либо
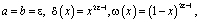 (7)
(7)
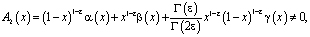 (8)
(8)
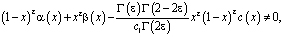
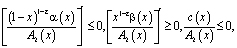 (9)
(9)
где 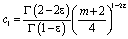 ,
, 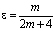 .
.
Теорему единственности можно доказать, предварительно доказав, что если U(x,y) является решением уравнения (1), удовлетворяющим однородным условиям (2), (3), то интеграл
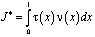
не может быть отрицательным, где
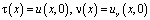 .
.
В этом случае единственность решения задачи (1)-(3) будет сразу следовать из соотношений [1,7].
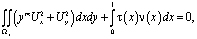
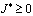 .
.
Покажем, что при выполнении условий теоремы 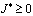 . Удовлетворяя решение задачи Коши [1] условию (3) в результате преобразований получим
. Удовлетворяя решение задачи Коши [1] условию (3) в результате преобразований получим
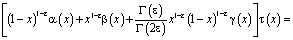
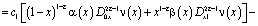
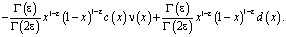 (10)
(10)
Пусть выполняются условия (7) – (9) теоремы единственности. Перепишем (10) в виде
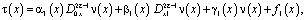 (11)
(11)
где 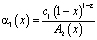 ,
, 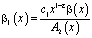
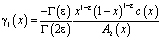 ,
, 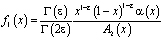 .
.
Докажем, что решение задачи (1) – (3) единственно. Для этого при (x)=0 покажем, что интеграл 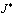 не может быть отрицательным. В самом деле,
не может быть отрицательным. В самом деле,
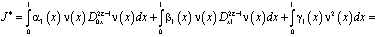
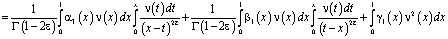 .
.
Воспользуемся формулой [10] для функции 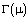 :
:
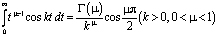 . (12)
. (12)
Полагая в ней 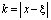 ,
, 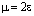 , получим
, получим
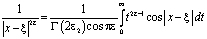 .
.
Отсюда поменяв порядок интегрирования, а затем, интегрируя по частям также как и ранее [3,8], получим
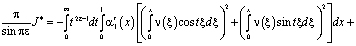
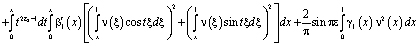 .
.
Очевидно, что при выполнении 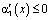 ,
, 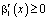 ,
, 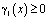 будет выполняться
будет выполняться 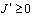 .
.
Пусть теперь выполняются условия (4) – (6) теоремы. Покажем, что и в этом случае 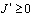 . При выполнении условий (4) теоремы соотношение между
. При выполнении условий (4) теоремы соотношение между 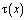 и
и 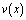 , принесенное из гиперболической части 2 области, будет иметь вид
, принесенное из гиперболической части 2 области, будет иметь вид
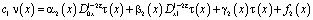 , (13)
, (13)
где
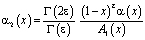 ,
, 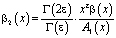 ,
,
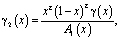
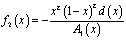 .
.
Рассмотрим интеграл
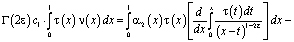
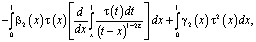
который с учетом обозначений
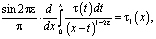
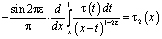
и формулы обращения [10] интегрального уравнения Абеля, а также (12) примет вид
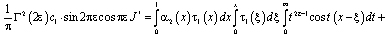
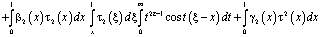 .
.
Поменяв порядок интегрирования, в результате несложных преобразований будем иметь
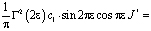
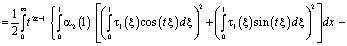
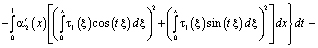
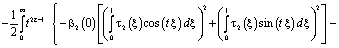
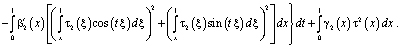
С учетом (5), (6) и того, что 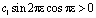 , из последнего заключаем, что интеграл
, из последнего заключаем, что интеграл 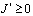 . Таким образом, при выполнении условий (4) – (6) или (7) – (9) теоремы единственности доказано, что
. Таким образом, при выполнении условий (4) – (6) или (7) – (9) теоремы единственности доказано, что
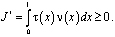
Отсюда заключаем единственность решения задачи.
Доказательство существования решения задачи. Переходя к доказательству существования решения задачи (1) – (3) относительно кривой σ будем предполагать, что 1) параметрические уравнения кривой σ, где s – длина дуги, отсчитываемая от точки B; функции x(s), y(s) имеют непрерывные производные x′(s), y′(s) на отрезке , необращающиеся одновременно в ноль; производные x″(s), y″(s) удовлетворяют условию Гельдера на [0, l], где l – длина σ; 2) в окрестности концов кривой σ выполнено условие
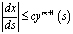 ,
,
где с=const.
Покажем сначала, что решение задачи (1) – (3) существует в случае, когда выполнены условия (4) – (6). Для этого потребуем дополнительно
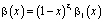 ,
, 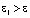
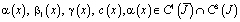 .
.
Фундаментальное соотношение между 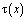 и
и 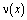 , принесенное на J из эллиптической части Ω1 смешанной области Ω имеет вид
, принесенное на J из эллиптической части Ω1 смешанной области Ω имеет вид
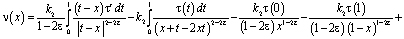
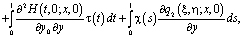 (14)
(14)
где свойства функций 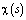 ,
, 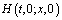 ,
, 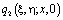 хорошо известны [1,7]. Исключив
хорошо известны [1,7]. Исключив 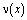 из (14) и (13) в результате замены
из (14) и (13) в результате замены 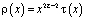 получим сингулярное интегральное уравнение
получим сингулярное интегральное уравнение
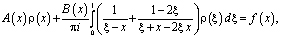 (15)
(15)
где
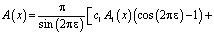
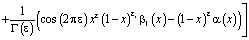 ;
;
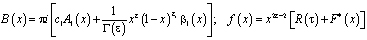 .
.
Последнее с учетом обозначения 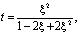
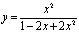 примет вид
примет вид
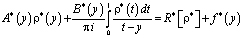 , (16)
, (16)
где
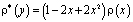 ,
, 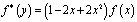 ,
, 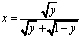 ,
,
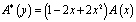 ,
, 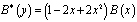 .
.
Таким образом, задача (1) – (3) эквивалентна в смысле разрешимости сингулярному интегральному уравнению (16). Так как
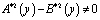 ,
,
то уравнение (16) нормального типа [6]. В соответствии с этим его решение может быть построено согласно общей теории [6]. Из свойств оператора R и функций, входящих в уравнение заключаем, что
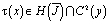 .
.
По найденному 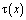 можно определить
можно определить 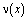 из соотношения (13). Затем решение
из соотношения (13). Затем решение 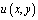 задачи (1) – (3) может быть найдено в области Ω2 как решение задачи Коши, а в области Ω1 по формуле
задачи (1) – (3) может быть найдено в области Ω2 как решение задачи Коши, а в области Ω1 по формуле
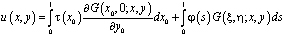 ,
,
где 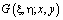 – функция Грина задачи (1), (2),
– функция Грина задачи (1), (2), 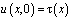 [1].
[1].
Существование решения задачи (1)–(3) при выполнении условий (7)–(8) теоремы доказывается также путем редукции к сингулярному интегральному уравнению, индекс которого равен нулю.
Библиографическая ссылка
Водахова В.А., Карданова М.Р., Эржибова Ф.А., Баттуев М.Б. ВНУТРЕННЕКРАЕВАЯ ЗАДАЧА ДЛЯ УРАВНЕНИЯ ГЕЛЛЕРСТЕДТА // Международный журнал прикладных и фундаментальных исследований. 2017. № 5-1. С. 30-35;URL: https://applied-research.ru/ru/article/view?id=11536 (дата обращения: 03.03.2026).

