Вопрос прогнозирования объема воды, накапливаемой в Токтогульском водохранилище (ТВ) относится к классу сложных задач, имеющих большое число независимых влияющих факторов. Для получения максимально точной математической модели необходимо сократить перечень этих факторов до минимума, поскольку от их количества трудоемкость моделирования возрастает как степенная функция. В связи с этим нужно произвести отбор по следующим критериям:
– факторы, не влияющие на целевую функцию и факторы коррелированные.
Для изучения данной проблемы используем информацию по объему воды в Токтогульском водохранилище по годам (табл. 1) [1].
Используя математические методы определим прогнозируемый объем воды с использованием множественного регрессионного анализа. Суть данного метода заключается в том, что для выбранного параметра определяется набор нескольких независимых факторов, влияющих на целевую функцию, и выводится зависимость в виде следующего уравнения (уравнения регрессии) [2, 3]:
у = а0 + а1 х1 + а2 х2 + а3х3 + а4х4 (1)
где у – значения общего показателя; а0 – свободный член; х1,х2,х3,х4 – независимые переменные; а1,а2,а3,а4 – переменные влияющие на общий результат.
С использованием данных, приведенных в табл. 1, на основе метода наименьших квадратов получим:
у = 12,315 + 0,039х. (2)
График этой функции представлен на рисунке.
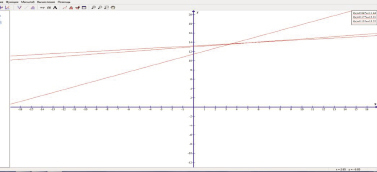
График функции
Если целевая функция у зависит от нескольких параметров (см. табл. 2), то зависимость у = f(x1,x2,x3,x4) можно получить с помощью других способов.
Таблица 1
Объем накопленных вод по годам в Токтогульском водохранилище
|
№ п/п |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
|
1 |
12,936 |
8,718 |
8,706 |
15,204 |
17,892 |
15,775 |
13,073 |
10,423 |
9,488 |
13,075 |
Таблица 2
Основание факторы оказывающие влияние на объема накопленной воды
|
Обозначения факторов |
Факторы |
Наименование факторов и их обозначения |
|
Х1 |
влияние погодных условий |
1 – сухая погода 2 – дождливая погода |
|
Х2 |
выброс воды с хозяйственных работ |
1 – для сельскохозяйственных работ 2 – технический выброс |
|
Х3 |
выработка электроэнергии |
1 – экспорт энергии в зарубежные страны 2 – для покрытия |
|
Х4 |
внутреннее потребление |
1 – непокрытые 2 – топливного покрытия |
|
Х5 |
состояние ГЭС |
1 – плохая 2 – хорошая |
Таблица 3
Сравнительный анализ расчётных и фактических значений объема воды ТВ по годам
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Годы |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
2014 |
2015 |
2016 |
|
Фактический объем, млрд м3 |
12,936 |
8,718 |
8,706 |
15,204 |
17,892 |
15,775 |
13,073 |
10,423 |
9,488 |
13,075 |
|
Расчетный объем, млрд м3 |
12,354 |
12,393 |
12,432 |
12,471 |
12,51 |
12,549 |
12,588 |
12,627 |
12,666 |
12,705 |
Производим расчет параметров уравнения с учетом табл. 1 и 2. Вычисления можно провести двумя способами:
1. Алгоритм расчета по скалярному способу:
составим матрицы, используя обозначения факторов из табл. 2:
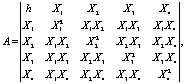 (3)
(3)
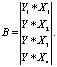 (4)
(4)
Решение находим с помощью следующего матричного уравнения:
Х = А-1 * В. (5)
Решив его, получим соответствующее уравнение множественной регрессии с конкретными числовыми значениями а0, а1, а2, а3, а4:
у = а0 + а1х1 + а2х2 + а3х3 – а4х4. (11)
С помощью уравнения (11) можно рассчитать объем воды, накопленный в разные годы в Токтогульском водохранилище.
Регрессионное уравнение для данного случая имеет вид:
у = 12,315 + 0,039х.
2. Запишем данные наблюдений и параметры математической модели в матричном виде.
Значения независимых переменных запишем в виде прямоугольной матрицы размерности nx (p + i) где p – количество факторов, n-фактическое количество объемов воды в разные годы.
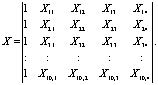 (6)
(6)
Здесь каждому столбцу матрицы (6) соответствует n-значений одного из факторов. Первый столбец состоит из «1», которые показывают значение переменных при свободном члене.
Из методов наименьших квадратов можно получить:
S = (XTX)-1XTY. (7)
При этом после определенных преобразований вектор S (вектор оценок) будет выглядеть следующим образом:
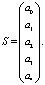
В результате получится уравнение регрессии для определения объема воды в ТВ:
у = а0 + а1х1 + а2х2 + а3х3 + а4х4. (8)
При этом уравнения типа (11) и (8), полученные по скалярному способу или по матричному методу, будут идентичными.
Таким образом, результаты проведенного исследования показали, что оба способа получения уравнения многофакторной регрессии являются адекватными и позволяют сделать вывод об их пригодности для прогнозирования объема накопления воды в ТВ, и тем самым могут быть использованы в технологических расчетах при производстве электроэнергии в электроэнергии Токтогульском ГЭСе.
Библиографическая ссылка
Адылова Э.С. ОПРЕДЕЛЕНИЕ ФАКТОРОВ И ПОКАЗАТЕЛЕЙ ОБЪЕМОВ ВОДЫ В ТОКТОГУЛЬСКОМ ВОДОХРАНИЛИЩЕ С ИСПОЛЬЗОВАНИЕМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ // Международный журнал прикладных и фундаментальных исследований. 2017. № 6-1. С. 9-11;URL: https://applied-research.ru/ru/article/view?id=11611 (дата обращения: 13.02.2026).
DOI: https://doi.org/10.17513/mjpfi.11611

