Постоянный рост скоростей обработки цифровой информации ставит все более строгие требования перед системами и алгоритмами обработки информации. Большую популярность получили методы кратномасштабного анализа сигналов и вейвлет преобразования [2-6]. В силу того, что значительная часть обрабатываемой информации является цифровой, особого внимания заслуживают методы целочисленной обработки информации. Данная задача наиболее эффективно решается с использованием модулярных кодов, в частности кодов системы классов вычетов (СОК) [1, 7].
Цель исследования
Применение модулярной арифметики позволит повысить эффективность дискретных вейвлет преобразований (ДВП) сигналов, обеспечивая их с высокой точностью и скоростью. Поэтому разработка метода целочисленного крупномасштабного анализа сигналов, базирующегося на алгебраических структурах, обладающих свойством кольца и поля, позволяющего повысить скорость ДВП, является актуальной задачей.
Материалы и методы исследования
Использование модулярной арифметики может позволить улучшить системы цифровой обработки информации путем увеличения скорости обработки данных. Применение систем остаточных классов в алгоритмах выполнения вейвлет преобразования позволит достичь больших преимуществ, чем выполнение преобразования в конечном поле.
В работах [3, 8] были рассмотрены вопросы применения дискретных вейвлет-преобразований в конечном поле. При построении матриц дискретного вейвлет преобразования Хаара применяются базисные функции Хаара hk(z), для которых величина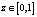 
задана на непрерывном замкнутом интервале.
Пусть необходимо выполнить ДВП Хаара для вектора отсчетов, содержащего 8 точек. Тогда матрица для выполнения дискретного вейвлет преобразования имеет следующий вид
(1)
Для того чтобы выполнить такое вейвлет преобразование в поле простого числа необходимо решить задачу поиска основания такого поля, в котором будет разрешимо сравнение второго порядка
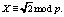(2)
Дальнейшим развитием целочисленного ДВП является применение модулярных кодов, в частности кодов СОК. В системе остаточных классов целое число A представляется в виде совокупности остатков,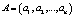 
, где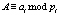 
; i = 1,2,…,n, полученных путем его деления на попарно взаимно простые модули pi. К основным достоинствам кодов СОК можно отнести высокую скорость и точность выполнения модульных операций, к которым относятся сложение, вычитание и умножение [1, 7, 9, 10]. Но данные операции широко используются при выполнении крупномасштабного анализа, согласно
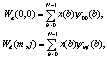(3)
где X = [x(0), x(1),…, x(N-1)] – входной вектор;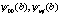 
– скалинг-функции ДВП; Wa(0,0) и Wd(m,j) – аппроксимирующие и детализирующие последовательности.
Применение кодов системы остаточных кодов позволяет свести одномерное вычисление ДВП по модулю р свести к многомерному вейвлет-преобразованию
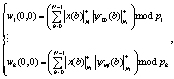(4)
где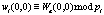 
; i = 1, 2, …, k.
При этом детализирующая последовательность будет иметь вид
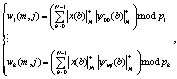(5)
где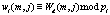 
; i = 1, 2, …, k.
Результаты исследования и их обсуждение
Допустим необходимо выполнить вейвлет преобразование Хаара над входным вектором данных из восьми элементов V = {1, 3, 2, 4, 0, 5, 1, 3}. Предлагается для выполнения такого преобразования использовать три основания для СОК р1 = 7, р2 = 17, р3 = 23. Все основания являются взаимно простыми. В поле каждого из оснований можно представить выражение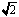 
в виде целого числа. Такое выражение будет иметь следующие значения в полях р1, р2, р3 соответственно 
.
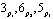Целочисленная матрица прямого преобразования будет иметь 8 строк и 8 столбцов, значение каждого элемента будет представлено тремя числами. Для такого представления необходимо вычислить целочисленные матрица преобразования для каждого из оснований. В этом случае матрицы будут иметь следующий
по модулю р1 = 7;
.
по модулю р2 = 17;
.
по модулю р3 = 23
.
Для удобства отобразим матрицу прямого вейвлет преобразования в СОК с основаниями р1 = 7, р2 = 17, р3 = 23, такая матрица будет иметь вид согласно выражению (8).
(6)
Имея матрицу описанную выражением (6) можно выполнить прямое вейвлет преобразование. Прямое преобразование в матричной форме сводится к перемножению матрицы (6) на вектор входных данных эту операцию описывает выражение
(7)
Для того чтобы выполнить умножение (7) необходимо входной вектор отсчетов представить в системе остаточных классов. В выбранной системе остаточных классов входной вектор будет иметь следующий вид
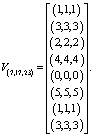(8)
Выполнив прямое преобразование можно выполнить обратное преобразование. Для этого необходимо получить матрицу обратного преобразования, которая будет иметь вид согласно выражению
(9)
В таком случае выражение (13) будет отображать обратное вейвлет преобразование в СОК.
Очевидно, что результат обратного преобразования дискретного вейвлет-преобразования в коде СОК совпадает с вектором входных данных.
Целочисленное вейвлет преобразование, выполняемое в системе остаточных классов имеет два больших достоинства. Первое заключается в том, что все вычисления выполняются с малыми числами, а также их можно распараллелить. Второе преимущество такого подхода в том, что применения системы остаточных классов позволяет использовать алгоритмы обнаружения и коррекции ошибок.
Заключение
В работе продемонстрирована возможность выполнения целочисленных вейвлет преобразований с применением системы остаточных классов, приведен пример прямого и обратного вейвлет преобразования входного вектора данных. Показаны достоинства такого подхода при решении задачи выполнения вейвлет преобразования, это возможность параллельного вычисления независимых частей преобразования. В качестве перспективы данной тематики можно отметить, что СОК позволяет не только обеспечить высокую точность и скорость выполнения ДВП, но этот модулярный код имеет возможность обнаруживать и корректировать ошибок за счет введения дополнительных оснований в СОК.
Библиографическая ссылка
Гиш Т.А., Дунин А.В., Калмыков И.А., Ефимович А.В., Кравцов А.Е., Харечкина Ю.О. РЕАЛИЗАЦИЯ ВЕЙВЛЕТ ПРЕОБРАЗОВАНИЙ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ // Международный журнал прикладных и фундаментальных исследований. – 2017. – № 6-1. – С. 22-26;URL: https://applied-research.ru/ru/article/view?id=11614 (дата обращения: 04.12.2024).