Надежные источники одиночных фотонов считаются одним из важнейших компонентов квантовых вычислительных устройств. В совместной работе учёных России и Италии в 2016 году доказано, что на основе дефектов в структуре алмаза на атомном уровне можно сделать очень эффективные источники одиночных фотонов, которые будут работать при комнатной температуре, причем даже более перспективные, чем аналогичные устройства на основе квантовых точек [11].
Исследовательская группа из швейцарского Института нанотехнологий и университета Базеля при помощи резонаторов, изготовленных из монокристаллического алмаза, создали наноустройство, в котором квантовая система объединена с механической колебательной системой. Используя это устройство, ученые впервые в истории продемонстрировали, что механическая система может использоваться для управления квантовым состоянием нанобъекта, включенного в резонатор, без использования сложных микроэлектронных структур. Благодаря высокой скорости колебаний спинов электронов, эта квантовая система практически не подвержена влиянию явления квантовой декогеренции, которое влияет на другие квантовые системы, заставляя спонтанно изменять их квантовое состояние [10].
Неудивительно, что в последнее время во многих ключевых экспериментах, продиктованных современной квантовой теорией, в качестве основного опытно-исследовательского материала выступает кристалл алмаза [3]. Обладая уникальными характеристиками и свойствами, этот кристалл в середине прошлого века был объявлен самым перспективным материалом предстоящего двадцать первого века. И в последние десять лет этот кристалл заявил о себе, как о действительно модельном кристалле физики конденсированного состояния и квантовой теории, подтверждая или уточняя многие проводимые эксперименты в этих областях.
Появились и интенсивно развиваются новые направления в науке, использующие не только узконаправленные пучки оптических фотонов с винтовым волновым фронтом [14], закрученные электроны [16] или пучки закрученного рентгена [9], но и акустические вихревые потоки [13]. На сегодняшний день орбитальный угловой момент волны (закручивание волны в пространстве, распространение волны с винтовым возмущением волнового фронта) является одним из самых фундаментальных физических параметров и в классической и в квантовой механике. И в этом направлении развития научного поиска кристалл алмаза проявляет себя наиболее эффективным объектом исследований.
В отличие от спинового углового момента, где есть только два возможных значения ±h, орбитальный угловой момент в принципе обеспечивает бесконечный диапазон возможно достижимых состояний [12]. Повышенный интерес к изучению подобных вихревых пучков связан с их необычными свойствами, позволяющими использовать эти пучки для создания волноводных структур и передачи информации, захвата и манипуляции микрообъектами, анализа фазово неоднородных сред с высокой степенью хаотизации, исследования микроструктуры цилиндрических объектов, изучения атмосферы планет и поиска планет вне солнечной системы и пр.
В данной работе приводится несколько примеров формирования коррелированных состояний квантовой среды алмаза при применении волнового способа механического воздействия на его структуру и создании в объёме алмаза квантовых волновых акустических потоков с орбитальным угловым моментом волнового фронта.
Способ воздействия
Для реализации представляемого способа воздействия используется оригинальное оборудование, разработанное по принципу двухосевого механического волнового воздействия на алмаз, где обрабатывающий инструмент имеет одну ось вращения α (с циклической частотой α) вокруг своего геометрического центра и одновременно совершает независимое эксцентричное перемещение как целое тело вокруг другой, но неподвижной оси α (с циклической частотой α). В результате мы имеем независимое двухосевое вращение и перемещение инструмента, которое обеспечивает сложное циклическое движение зёрен абразива относительно обрабатываемой поверхности алмаза, описываемое уравнениями второго порядка [6].
Расстояние (rа) между подвижной β и неподвижной β осями вращения и перемещения является аппаратурным фактором и выбирается в соответствии с используемым алгоритмом обработки. Ось вращения β является центром инерции обрабатывающего инструмента, диаметр рабочей поверхности которого выбирается в зависимости от поставленной задачи воздействия и имеет размер в несколько раз больше, чем (ra). Линейная скорость движения зерна абразива в точке контакта инструмента с алмазом в случае двухосевого движения инструмента является периодической функцией и изменяется в пределах линейных скоростей движения зёрен абразива V1 и V2, задаваемых радиусом эксцентрического перемещения (ra), при этом V1 – V2 = V. Диаметр инструмента и скорость его вращения задают требуемую линейную скорость движения абразивного зерна, взаимодействие которого с поверхностью кристалла в нашем случае не превышает предел её упругости (~10,5•1011 Па), что сводит к минимуму образование микросколов по моделям Герца и Ауэрбаха [2].
Параметр ΔV как приращение линейной скорости движения инструмента относительно обрабатываемой поверхности алмаза есть величина постоянная в любой точке контакта обрабатывающего инструмента с кристаллом и зависит только от (rа). Следовательно, и тангенциальное ускорение всех зёрен, участвующих в процессе генерации возмущающих волн в обрабатываемом алмазе, будет также инвариантно относительно координат контакта. Критерий пространственного постоянства ΔV является определяющим фактором при создании когерентного флуктуирующего волнового поля упругих деформаций в объёме алмаза.
Перемещение обрабатывающего инструмента по окружности (O = 2rа) относительно выбранного кристаллографического направления воздействия на поверхность алмаза приводит к циклическому изменению направления движения и величины линейных скоростей зёрен абразива (в пределах ΔV), взаимодействующих с атомными кристаллографическими плоскостями обрабатываемого кристалла. В этом случае возникают условия для образования углового момента формируемого потока энергии упругой деформации в приповерхностной области кристалла, т.е. движение (выравнивание) энергии между равнозначными, но разделёнными в пространстве кристаллографическими направлениями воздействия [4].
Этот образующийся вихревой поток имеет угловой момент, который передаётся формируемым волнам упругих деформаций. Образованные квантовые волновые потоки имеют момент вращения, т.е. возникает волновой поток с орбитальным угловым моментом волнового фронта. Такого рода возмущения обуславливают вихревой характер распространения волновой энергии [7]. Взаимодействие квантовых потоков волн упругих деформаций, обладающих орбитальным угловым моментом волнового фронта, с квантовой средой алмаза и создают уникальную динамическую коррелированную квантовую среду в его объёме.
Основные следствия при использовании разработанного способа воздействия:
- определяющее влияние ΔV на создание сильнонеравновесных волновых процессов в объёме алмаза;
- стабильность параметров α и β и соответственно параметра ΔV – условие когерентности протекания процесса воздействия;
- управление частотой перемещения инструмента – управление формируемой функцией состояния квантовой динамической среды и влияние её на энергию квантовых флуктуаций.
Частота α вращения инструмента в разработанном оборудовании с ЧПУ может находиться в диапазоне 0÷10000 об/мин., частота β варьируется в пределах 0÷120 Гц. Конкретные параметры и соотношения частот в случае независимого двухосевого механического движения инструмента определяются поставленной целью и задачей при применении этого нового метода воздействия на кристаллы алмаза.
Алгоритмы воздействия
В данной работе использовались алмазные пластины весом 0.06 карат, размером 3х3х0.4 мм, вырезанные в ориентации (100) из монокристаллов синтетического алмаза, выращенных методом HPHT (High Temperature High Pressures). При выращивании синтетических алмазов этим методом характерно развитие нескольких секторов роста, представленных кубическими {100}, октаэдрическими {111}, ромбододекаэдрическими {110} и тетрагонтриоктаэдрическими {113} секторами роста. Схематическое распределение указанных секторов по объему кристалла в форме усеченного октаэдра приведено на (рис.1). На этом рисунке также приведено характерное секторальное строение пластин, вырезанных по сетке куба из различных частей данного кристалла (рис. 1, б и в).
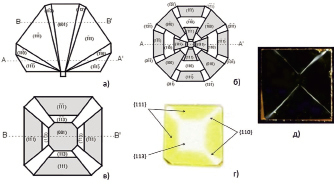
Рис. 1. Секторальное строение монокристаллов синтетического алмаза
Различия в эффективности захвата фоновых примесей разными секторами роста может приводить к возникновению в кристалле областей с существенным отличием физических характеристик. С этой точки зрения наибольшую неоднородность имеют пластины, вырезанные из центральной части кристалла (рис. 1, б).
Основными фоновыми примесями в кристаллах синтетического алмаза, выращенных в системах металла-растворителя на основе никеля, являются атомы азота и никеля. В работе (R.C.Burns et.al., 1990) показано, что для кристаллов синтетического алмаза примесь азота распределяется по секторам роста следующим образом:
N {110}: N {113}: N {100}: N {111} @ 1 : 8 : 50 : 100.
Концентрация примеси азота в секторе роста {111}, как правило, находится в интервале 100÷300 ppm. Содержание азота слабо зависит от скорости роста кристаллов, но зависит от температуры в реакционной зоне. По нашим данным при увеличении температуры синтеза с 1350 °С до 1500 °С происходит снижение содержания примеси азота в кристалле в 1,5-2 раза.
В синтетических алмазах, выращенных при невысоких температурах, примесь азота в основном присутствует в форме одиночных атомов азота в положении замещения (С-дефект). Для областей кристалла с высоким содержанием С-дефектов в спектрах наблюдается характерный край примесного поглощения в диапазоне 430÷480 nm. В результате этого сектора роста {111} окрашены в насыщенный желтый цвет. Окраска секторов роста {100} менее интенсивна, а сектора роста {113} и {110} – бесцветны (рис. 1, г). Пластина аналогична пластине на (рис. 1, в). На рис. 1, д – изображение пластины в поляризованном свете в скрещенных поляризаторах.
Для кристаллов синтетического алмаза, выращенных при низких температурах (Т - 1450 °С), примесь никеля захватывается преимущественно в виде одиночных атомов, которые располагаются как в узлах решетки, так и в междоузлиях. Примесь никеля захватывается только секторами роста {111}. В остальных секторах никель не регистрируется. Эффективность захвата примеси никеля зависит от температуры и от линейной скорости роста грани [16].
В данной работе волновому воздействию подвергались пластины алмаза (рис. 1, г, 1, д), соответствующие зоне кристалла (рис. 1, в), из которой были вырезаны эти пластины.
Белый крест, наблюдаемый на приведённом изображении пластины, образован секторами роста {110}, т.е. содержит на 2 порядка меньше примеси азота, чем соседние области, принадлежащие секторам роста {111} (содержание примеси азота в секторе {111} порядка 100 ppm). Кроме того, сектор {110} не содержит примесь никеля. Характерное содержание никеля в секторе {111} для этой зоны кристалла – 2/4 ppm.
Пластина алмаза, при постановке её на обрабатывающую систему, ориентировалась относительно траекторий движения зёрен абразива обрабатывающего инструмента, диаметр которого составлял ~ 40 мм, таким образом, чтобы обеспечить максимально эффективное упругое воздействие на заданные кристаллографические направления {100} относительно выбранного направления обработки {110} (позиция 1, рис. 4).
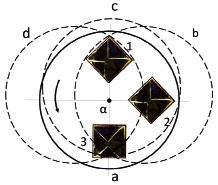
Рис. 2. Схематическое изображение процесса волнового воздействия на пластину алмаза относительно выбранного направления обработки. 1, 2, 3 – положение пластины относительно направления движения зёрен абразива; a, b, c, d – фрагменты положения перемещающегося инструмента, стрелка показывает направление вращения инструмента
На этом рисунке приведены положения алмазной пластины относительно поверхности обрабатывающего инструмента (относительно траекторий движения зёрен абразива), фрагменты (a, b, c, d) периодического эксцентричного положения обрабатывающего инструмента относительно кристаллографических направлений воздействия. При круговом перемещении инструмента вокруг оси (на рисунке не показана), происходит изменение направления движения зёрен абразива относительно заданных кристаллографических направлений {100} пластины алмаза. Например, инструмент перемещается в положение b, где происходит эффективное воздействие на кристаллографические плоскости (010) с максимальной передачей энергии упругих деформаций в этом направлении. В положении инструмента d происходит эффективное воздействие на кристаллографические плоскости (001) с максимальной передачей энергии упругих деформаций уже в этом направлении. В положении инструмента a и c происходит эффективное упругое воздействие на выбранное направления обработки {110}. При таком перемещении инструмента меняется и радиус (rа) расстояние положения пластины на поверхности инструмента от оси его вращения, что приводит к периодическому изменению линейной скорости движения абразива, т.е. формированию V.
Такое циклическое изменение линейной скорости абразива и периодичность изменения траекторий его движения относительно кристаллографической ориентации обрабатываемого кристалла мы назвали симметричное воздействие. В процессе воздействия обороты вращения инструмента составляли α ~ 6350 об/мин, частота перемещения инструмента β ~ 7 Гц.
Следует заметить, что в приведённом примере воздействия рёбра пластины являются заданными направлениями, а выбранное направление – одна из диагоналей {110} прямоугольной пластины. Вокруг этой диагонали пластины и происходит симметричное воздействие на семейство плоскостей {100} (позиция 1, рис. 4). Чтобы эффективно воздействовать на другую диагональ пластины, необходимо развернут пластину на 90 °, либо переместить алмазную пластину в позицию 2 на поверхности обрабатывающего инструмента.
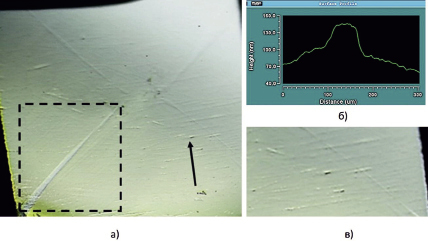
Рис. 4. Изображения поверхности пластины алмаза после воздействия (а) с отмеченным фрагментом, б) – профиль поверхности фрагмента в интерференционном профилометре, в) – увеличенный участок поверхности, отмеченный стрелкой
Если выбранным направлением воздействия определить кристаллографические плоскости {100}, а заданными направлениями {110}, то пластину кристалла алмаза необходимо ориентировать относительно траекторий движения абразива разворотом, например, как показано на позиции 3 рис.4, чтобы обеспечить максимальный эффект по алгоритму симметричного воздействия на заданные кристаллографические направления {110} относительно выбранного направления обработки {100}.
Результаты эксперимента
После обработки поверхности алмазной пластины в течении 60 мин процесс воздействия был продолжен на противоположной (второй) стороне пластины. В этом случае, при сохранении всех остальных параметров обработки, были изменены только направление вращения α и направление перемещения β инструмента на противоположное. Это было сделано с целью сохранения направленности вектора орбитального углового момента при формировании волнового фронта акустических волновых потоков в объёме алмаза в том же направлении, что было заложено при обработке первой поверхности алмазной пластины. В этом случае были максимально сохранены общие условия формирования определённой функции состояний динамической квантовой среды алмаза. На рис. 3 приводится изображение алмазной пластины после волнового воздействия.


Рис. 3. Изображения пластины алмаза после волнового воздействия: а – изображение пластины в отражённом свете, б – изображение пластины в поляризованном свете в скрещенных поляризаторах
При анализе изображений алмазной пластины после волнового воздействия обращает на себя внимание тот факт, что белый крест, наблюдаемый на изображениях пластины до волнового воздействия, полностью отсутствует.
Алмаз является оптически изотропным кристаллом и не дает эффекта двойного лучепреломления света. Если в кристалле алмаза отсутствуют внутренние напряжения, то в поляризованном свете в скрещенных поляризаторах кристалл будет наблюдаться, как темный кристалл. Проявление эффекта двулучепреломления в алмазе объясняется либо остаточными механическими напряжениями, либо неравномерным зонально-секторальным распределением примесей по его объему. В статье Кайзера и Бонда [15] указывается, что азотные примеси вызывают расширение кристаллической решетки алмаза. Вхождение азота, образующего дефекты в решетке алмаза, изменяет его кристаллографические параметры и в зонах с разным содержанием примеси азота возникают неодинаковые поля напряжений. Этот факт неравномерного распределения азотных примесей по объёму кристалла и образование полей внутренних напряжений в объёме алмаза и приводит к появлению эффекта двулучепреломления при наблюдении исследуемой пластины в поляризованном свете в скрещенных поляризаторах.
После волнового воздействия на приведённых изображениях пластины алмаза в отражённом свете (рис. 3) мы наблюдаем белый крест, образованный секторами роста {110}. Но на изображениях пластины в поляризованном свете в скрещенных поляризаторах (рис. 3, б) картина двулучепреломления отсутствует. Подобный факт говорит о том, что пластина алмаза в этом случае является изотропным кристаллом и не дает эффекта двойного лучепреломления, т.е. поля внутренних напряжений в объёме алмазной пластины после волнового воздействия полностью отсутствуют.
На (рис. 4) приводится изображение поверхности пластины алмаза в оптическом микроскопе (а) в положении её оптической оси, близком к зеркальному отражению поверхностью алмаза падающего света.
Наблюдаемые в оптическом микроскопе морфологические изменения поверхности алмазных пластин после волнового воздействия, проявляющиеся в виде объёмных поверхностных конфигураций, совпадающих формой и пространственным положением на алмазной пластине с секторами роста {110}, подтверждается данными оптического профилометра (рис. 4, б), где высота фрагмента наблюдаемой конфигурации составляет ~ 145 нм. Применялся интерферометр (оптический профилометр) белого света ZygoNewView 5000.
На алмазной пластине после волнового воздействия, выполненного по алгоритму, где выбранным направлением воздействия определялись кристаллографические плоскости {100}, а заданными направлениями {110}, наблюдается аналогичная ситуация (рис. 5). В этом случае высота образовавшихся поверхностных конфигураций по направлениям {110} составляет ~ 225 – 250 нм.

Рис. 5. Морфологические изменения поверхности пластины алмаза (а) после волнового воздействия (изображение в оптическом микроскопе), где выбранным направлением воздействия определялись кристаллографические плоскости {100}, а заданными направлениями {110}, б) – профиль выделенной поверхности алмазной пластины в интерференционном профилометре, в) – увеличенный участок поверхности, отмеченный стрелкой
Обсуждение результатов
Квантовые корреляции составной системы связаны с когерентным суперпозиционным состоянием составных квантовых подсистем. Существующие в кристалле подсистемы (электронная, нуклонная, фононная и пр.) при обычных условиях находятся в хаотическом (сепарабельном) состоянии (коэффициент корреляции в этом случае стремится к нулю), т.е. имеются различные моды собственных внутренних квантовых флуктуаций в кристалле. Эта ситуация в кристалле сохраняется до момента циклического воздействия обрабатывающего инструмента на его поверхность и перехода кристалла в неравновесное состояние. В момент формирования динамического квантового поля энергии упругих деформаций кристалла (формирование фононного поля) происходит взаимная синхронизация разных состояний в кристалле, что приводит к синхронизации флуктуаций импульса и все составляющие кристалл подсистемы приходят в коррелированное состояние с формированием общей фазы флуктуаций составной системы с коэффициентом корреляции отличном от нуля [1].
Особую роль при распространении квантового волнового потока энергии упругих деформаций в объёме кристалла начинает играть орбитальный угловой момент его волнового фронта. Скорость звука в алмазе составляет ~ 18 350 м/с, в проведённом эксперименте частота воздействия инструмента на поверхность кристалла ~ 7 Гц, длина волны распространяющегося квантового волнового потока в этом случае составляет ~ 2571 м. Поскольку длина распространяющейся волны во много раз превышает размеры алмаза, то колебания (флуктуации) всего кристалла происходят как единое задаваемое динамическое состояние всей составной системы алмаза. Это и является определяющим фактором при формировании единого фазового пространства всей динамической системы кристалла. Подобное состояние соответствует состоянию квантового фазового перехода [5].
Передавая энергию углового момента кристаллической решётке кристалла волновые потоки влияют на энергию ковалентных связей её атомов. Особенно эффективно концентрация этой энергии происходит на дефектах или неоднородностях состава кристаллической структуры алмаза. Сектора роста {110}, содержащее на 2 порядка меньше примеси азота, чем соседние намного большие по размеру области секторов роста {111}, имеют более плотное состояние своей атомной структуры и соответственно более высокочастотный диапазон своих флуктуаций в этом объёме. Поскольку неравновесное состояние всей динамической системы алмаза приводит к изменению атомных связей всей структуры, то в областях взаимодействия секторов роста {110} и {111}, за счёт наибольшего вклада энергии углового момента возникает градиент движения (диффузии) всей сформированной зоны с пониженной концентрации азотных дефектов в область её «наибольшего комфорта», т.е. на поверхность алмазной пластины. При этом вполне естественно исчезают области внутренних напряжений кристалла.
Движение (выталкивание) объёма секторов роста {110} на поверхность алмазной пластины при неравновесном состоянии кристалла происходит симметрично в обоих направлениях к поверхности от центральной зоны пластины. Поскольку на одну из поверхностей алмазной пластины в этот момент воздействует работающий инструмент, то наблюдаемые объёмные поверхностные конфигурации фиксируются только на одной стороне алмазной пластины, которая была обработана в первую очередь.
Следует заметить, что после воздействия инструмента на поверхности пластины между секторами роста {110} наблюдается сформировавшийся морфологический рельеф в виде неких объёмных «барханов», ориентация которых соответствует заданным направлениям воздействия {100} или {110} (рис. 4, в и рис. 5, в соответственно). Этот рельеф не связан со следами воздействия абразива работающего инструмента, поскольку обрабатывалась противоположная поверхность кристалла и в этот момент непосредственный контакт инструмента с этой поверхностью отсутствовал.
При произвольной ориентации пластины (без симметричного воздействия) и отсутствия условий формирования вихревого потока в её объёме (при обработке второй поверхности пластины значения направления движения α и β не изменялись) вышеизложенные эффекты морфологической перестройки поверхности связанных с секторами роста не зафиксированы.
Заключение
Использование двухосевой системы волнового механического воздействия на структуру алмаза и создание в объёме волновых акустических потоков с орбитальным угловым моментом волнового фронта приводит к формированию особого динамического коррелированного состояния квантовой среды в объёме алмаза.
Подобный подход позволяет получать кристаллы алмаза с новыми кристаллофизическими параметрами, с новыми сформированными квантовыми эффектами [5], что делает возможным создание на этой основе абсолютно нового класса приборов.
Авторы благодарят Шаронова Геннадия Викторовича (Институт прикладных физических проблем им. А.Н. Севченко, г. Минск, Республика Беларусь) за предоставленные материалы и плодотворные дискуссии.
Библиографическая ссылка
Карасёв В.Ю., Неволин В.К., Заведеев Е.В. ДИНАМИКА ФОРМИРОВАНИЯ КОРРЕЛИРОВАННЫХ СОСТОЯНИЙ КВАНТОВОЙ СРЕДЫ КРИСТАЛЛОВ АЛМАЗА ПРИ МЕХАНИЧЕСКОМ ВОЛНОВОМ ВОЗДЕЙСТВИИ // Международный журнал прикладных и фундаментальных исследований. 2017. № 6-1. С. 66-73;URL: https://applied-research.ru/ru/article/view?id=11624 (дата обращения: 13.02.2026).

