Физике транспорта в видеоиграх посвящено довольно мало исследований. В статьях, которые можно найти на просторе интернета, физика транспортного средства описывается очень поверхностно. Как правило, в этих статьях описываются основы. Таким образом, программист, отвечающий за создание транспортного средства для видеоигры, находится в информационном вакууме и должен использовать различные хитрости и упрощения в симуляции физики.
Большинство существующих моделей и теорий сформулированы таким образом, что их применение практически невозможно для использования в видеоиграх. Остальные используют настолько ресурсоемкие методы симуляции, что становится невозможен их контроль и адаптация под нужды разработчиков и игроков.
Исходя из вышесказанного, было принято решение создать упрощенную модель взаимодействия надводных судов с водой, которая учитывала бы все важные параметры корабля.
Исследование способов взаимодействия корпуса судна с водой
Прежде чем перейти к разработке самого алгоритма, необходимо упомянуть такую вещь, как выталкивание. При погружении тела в жидкость создается давление, тем самым к поверхности тела прилагается сила. В зависимости от увеличения давления, увеличивается и сила. Сила – результат движения большого количества частиц воды в жидкости, которые упруго ударяются о поверхность тела. Воздействие этой микроскопической силы заметно даже при отсутствии какого-либо движения в каком-либо направлении, а значит при неподвижном судне, поэтому эта сила называется гидростатической. Если сложить силу всех атомов или молекул, которые ударяются о поверхность корабля, то получившаяся сила окажется перпендикулярна поверхности. Также стоит упомянуть, что с увеличением глубины давление увеличивается. Однако само по себе давление определенного направления не имеет, давление над определенной точкой будет зависеть от общей глубины, даже если над этой точкой нет жидкости. Тут стоит уточнить, что в случае, если на заданной глубине давление в точке было ниже, чем в других точках на той же глубине, то в эту точку, в которой меньшее давление, переместилась очень быстро вода из тех точек, в которых она подвергается большему давлению, таким образом восстанавливая равномерное давление на данной глубине. Естественно, что такое не происходит. Поднятию воды с повышенным давлением с большей глубины на глубину с пониженным давлением препятствует гравитация. Поэтому при погружении существует увеличивающийся градиент давлений.
Гидростатическая сила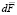 
, действующая на элементарную площадку площадью dS, задается следующим образом:
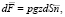
где p – плотность воды, z – глубина воды, а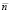 
– нормаль к поверхности.
Для расчета выталкивающих сил существуют два способа. Первый способ – рассчитываем, насколько погружается тело, и определяем центр его тяжести. Второй способ – рассчитываем приложенные к погруженной поверхности силы. Назовем первый способ объемным, а второй – поверхностным. Если не использовать аппроксимацию, то оба способа требуют определить координаты где пересекаются вода и корпус судна. Звучит довольно сложно, особенно в случае, когда вода не в спокойном состоянии. Такой расчет требует много времени и ресурсов, поэтому, как правило, используют объемные примитивы, то есть вместо того, чтобы рассчитывать то, как пересекается сложная фигура и поверхность воды, рассчитывается объем той части примитивов, которая погружена в воду. Объем примитивов можно даже определить аналитически, то есть в теории бесконечно точно.
При использовании сфер для аппроксимации корпуса судна могут возникнуть большие сложности, как минимум из-за того, что потребуются сферы различного диаметра в большом количестве. Еще одной проблемой является то, что между сферами возникают значительные пустоты. Существует ограничение на то, сколько сфер возможно упаковать в заданный объем. Наличие пустот приводит к непостоянству при выталкивании.
При поверхностном способе не нужно замыкать объем, необходимо только суммировать силы. Преимущество объемного способа заключается в том, что можно посчитать сразу несколько объемов, например, при расчете корпусов катамарана.
На этом закончим с исследованием способов взаимодействия корпуса судна с водой и перейдем непосредственно к построению алгоритма. Так как поверхностный подход более универсален, именно он и был выбран для алгоритма.
Разработка алгоритма
Основная задача алгоритма – определить координаты, где пересекаются поверхность судна и поверхность воды. После рассмотрения варианта Эдварда Хэлберта [1] было принято решение реализовать точное решение, которое учитывало бы все варианты пересечения треугольника и воды. Так как в теории разделить треугольник поверхностью можно большим количеством способов, то реализация необходимого решения довольно сложна. Треугольник может прорезаться поверхностью воды в нескольких местах, через центр треугольника может проходить поверхность воды, треугольник может не касаться воды ни одной своей стороной или быть полностью или частично погружен любой из вершин. В каждом из этих случаев необходимо разбить погруженный участок на треугольники (триангулировать), но так как такие участки не всегда бывают выпуклыми, триангуляция бывает затруднительна. К тому же такие случаи происходят довольно часто. Даже при, казалось бы, спокойной воде они происходят очень часто и должны обрабатываться так, чтобы результатом не стала нереалистичная дискретность.
При разработке такого точного алгоритма стало понятно, что его необходимо упростить, иначе он станет таким же, как и уже существующие.
Оптимизировав алгоритм, получили следующую структуру: сеткой из треугольников аппроксимируется плавающее тело. Определяется высота каждой вершины корпуса над водой. Тело находится под водой, если высота отрицательная. Это одно из наших упрощений. В некоторых ситуациях все три вершины могут находиться под водой, но при этом непосредственно поверхность треугольника может быть над водой. Кроме того, если бы пересекаемые области были вогнутыми, то быстрая триангуляция усложнилась. Обработка подобных случаев приводит к большим затратам времени при разработке и необходимости в большой производительности при работе игры.
Кроме того, можно считать, что треугольник полностью под водой, если часть площади находится над водой, но при этом все три вершины находятся под водой. В случае, если под водой находится одна или две вершины, треугольник можно разделить на две части: одна часть будет находиться над водой, а вторая – под водой. Если погруженных вершин две штуки, то погруженную часть необходимо дополнительно триангулировать.
После того, как алгоритм сработает, мы должны получить список треугольников, которые погружены под воду. После этого необходимо рассчитать действующие на треугольники гидростатические и гидродинамические силы.
Основное преимущество данного подхода в том, что вершины обрабатываются за один проход. После чего мы получаем всю информацию, которая нужна для обработки погруженных треугольников. Максимальное число погруженных треугольников равняется двойному количеству треугольников в корпусе. Таким образом, мы заранее можем выделить необходимую память в виде обычного массива.
Оттого, каким способом произведена симуляция воды в игре, зависит способ, который будет выбран для определения высоты каждой вершины над водой. В некоторых случаях можно просто замерять высоту воды, в других случаях, например, если используются методы, основанные на быстром преобразовании Фурье [2], замер высоты воды может оказаться ресурсоемок, поэтому можно замерить высоту воды в точках, равноудаленных от тела, тем самым создавая карту высот.
Запрос высоты точки включает в себя определение квадратной ячейки, на которую точка проецируется вниз и определение того из двух треугольников ячейки, на который падает проекция. Определение опорной ячейки выполняется значительно быстрее, если карта высот привязана к осям координат.
Узнав, на какой треугольник проецируется точка, мы можем быстро определить высоту точки над или под треугольником, если мы используем уравнение плоскости, заданной треугольником. Алгоритм предварительно рассчитывает все уравнения плоскости треугольников ячеек перед его использованием для расчета высот над водой вершин корпуса судна.
В случае, если какая-то часть вершин треугольника оказывается под водой, а другая часть оказывается над водой, треугольник необходимо разделить соответственно на два куска, первый будет полностью погружен под воду, а второй будет полностью находиться над водой. Есть способ для упрощения такого разрезания. Он более быстрый и непрерывный при расчетах. Под «непрерывностью» понимается отсутствие таких ситуаций, при которых даже небольшое изменение высоты вершины приведет к неожиданным и достаточно сильным изменениям погруженной области.
Итак, соберем уже все имеющиеся у нас данные и кратко опишем структуру алгоритма:
- чтобы вода следовала за водным транспортом, в каждом кадре обновляется положение воды;
- определяется высота воды для каждой точки в сетке;
- вычисляется уравнение плоскости для треугольников, которые образованы точками сетки;
- рассчитывается высота вершины корпуса над водой;
- применяется алгоритм разрезания для каждого треугольника;
- для всех погруженных треугольников рассчитываются действующие на них силы.
Тестирование алгоритма на трехмерной модели
Unity – Unity – это инструмент для разработки двух- и трёхмерных приложений и игр, но кроме, того он подходит для создания архитектурных визуализаций [3], виртуальных тренажеров [4] или моделирования поведения физических объектов.
Есть несколько способов создать надводный транспорт в Unity, например:
– просто добавить Box Collider на модель, размещенную так, что ее дно будет ниже ватерлинии;
– использовать встроенный в Unity Wheel Collider;
– создать модель, использующую реальные физические законы и уравнения на их основе. Собственно именно этим мы и занимались в предыдущей главе.
Прежде чем преобразовать выведенные нами уравнения, необходимо создать простую сцену в Unity.
Создаем две плоскости. Одна из них будет дном моря, вторая – водой. В будущем добавим волны. Воду расположим на позиции 0 оси координат y, а дно – на пять метров ниже (позиция –5 оси координат y). Уберем Mesh Collider с плоскости, которая отвечает за воду.
Теперь создадим лодку. Для начала в роли лодки нам подойдет обычный куб. С ним легче тестировать полученные уравнения. Создав куб, оставим все настройки как есть. Добавим Rigid Body и изменим массу куба на 800 килограммов, а параметр drag – на 0,5.
Добавим в качестве дочернего объекта пустой Game Object, который пусть называется UWMesh. К этому объекту в дальнейшем добавится подводная часть куба, путем добавления Mesh Filter и Mesh Renderer к UWMesh.
Чтобы корабль легче было отличать от воды, необходимо добавить материалы. Создадим три материала, один для воды, один для дна, и один для подводной части корабля. Если мы попытаемся сейчас запустить сцену, то увидим, что куб проваливается сквозь плоскость воды на дно. Это нехорошо, так как нам нужно, чтобы он плавал.
Итак, наш куб отправляется на дно океана. Чтобы этого не происходило, а лодка оставалась на поверхности, необходимо добавить силу плавучести.
В предыдущей главе подробно разбирался алгоритм разрезания модели на треугольники, выводились формулы и т.д. Все это было преобразовано в код и разбито на следующие скрипты: BoatPhysics, ModifyBoatMesh, TriangleData, WaterController.
Итак, теория переведена в практику. Осталось задаться вопросом: «А верно ли мы все рассчитали? Поплывет ли модель? Насколько она реалистична?» Ранее мы создали куб весом в 800 килограммов. Добавляем скрипты, запускаем сцену и видим, что куб плавает. Хорошо, но насколько реалистично он плавает? Для ответа на этот вопрос надо вспомнить закон Архимеда: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела. То есть, если наш куб со стороной один метр будет весить более одной тонны, то в воде, чья плотность 1000 кг/м3, он утонет. Можно попробовать изменить вес нашего куба и заметить, что он действительно при весе больше тонны уходит под воду, а при уменьшении веса поднимается на поверхность.
Таким образом, наш код будет работать с любой моделью любой формы, не только с кубом.
Выводы
Приведен алгоритм для расчета пересечения с поверхностью воды произвольной сетки и вычисления действующих на тело, которое описано этой сеткой, гидростатических сил. Было добавлено затухание для стабилизации системы, так как при изначальном алгоритме корабль колебался бы вверх-вниз, словно на пружине, т.е. выталкивался в воздух из воды, а после под воздействием гравитации погружался и снова выталкивался.
Водный транспорт представляет из себя триангулированный меш. Поверхность воды аппроксимируется с полем высот, и определяется та часть судна, которая находится под водой, через список погруженных треугольников, при помощи быстрого алгоритма пересечения поля высот с аппроксимированным треугольником. Каждый треугольник меша создает от 0 до 2 полностью погруженных треугольников.
Алгоритм не замыкает погруженный объем. Посредством этого алгоритма может быть быстро определена ватерлиния при условии своевременного получения ее сегментов в коде определения пересечения.
При распределении на погруженной части судна гидростатического давления было принято, что давление на поверхности погруженного треугольника постоянно. Таким образом движение судна является результатом не только гидростатических сил. Следует учитывать, что чем больше треугольники корпуса, тем приближение грубее. Однако, данная модель работает и на низкополигональных моделях.
Разработанную модель можно применить практически для всех видов, форм и размеров водных транспортов. Модель способна работать как в условиях штиля, так и при сильном шторме без значительной дополнительной доработки.
Разработанная модель позволяет работать с совершенно разными типами корпусов, проявляя правильное поведение в воде с движущей силой.
Библиографическая ссылка
Скворцов А.В., Пирогова А.А. РАЗРАБОТКА АЛГОРИТМА ВЗАИМОДЕЙСТВИЯ НАДВОДНОГО ТРАНСПОРТА С ВОДОЙ // Международный журнал прикладных и фундаментальных исследований. – 2017. – № 6-2. – С. 201-204;URL: https://applied-research.ru/ru/article/view?id=11648 (дата обращения: 23.11.2024).