К основным видам карьерного транспорта, широко применяемым на открытых горных работах, относятся железнодорожный карьерный транспорт, автомобильный карьерный транспорт и конвейерный карьерный транспорт, применяемые самостоятельно, а также комбинированный транспорт, предусматривающий различное сочетание основных видов транспорта. Реже на карьерах используются канатный (скиповые и автомобильные подъемники и канатные подвесные дороги), гидравлический, гравитационный, скреперная доставка и новые виды транспорта (конвейерные поезда, крутонаклонные конвейеры, воздушный транспорт и другие). По характеру грузопотоков, различают цикличный (железнодорожный, автомобильный, скиповой) и непрерывный (конвейерный, конвейерные поезда) виды транспорта [1].
Автомобильный карьерный транспорт благодаря своим преимуществам в сравнении с другими видами транспорта в настоящее время является наиболее распространенным в Казахстане и странах всего мира. Опыт применения автомобильного транспорта подтвердил его высокие технико-экономические показатели в определенных горнотехнических условиях.
Цель исследования
Оценка работоспособности системы тягового электропривода (СТЭП) автомобильного карьерного транспорта в различных горно-геологических и климатических условиях Центрального Казахстана. Проведение натурных исследований СТЭП, а также испытания системы на имитационных стендах, выполняемые с целью оценки ее параметров в эксплуатационных условиях, требуют значительных затрат времени и средств. В связи с этим в КарГТУ на базе математической модели многокомпонентной системы «Карьерный автомобиль – условия и режимы движения – системы тягового привода» разработаны алгоритм и машинные программы расчетного исследования системы тягового электропривода (СТЭП).
Методика исследования предусматривает экспериментальную проверку математической модели, выполнение расчетной оценки работоспособности агрегатов тягового электрооборудования СТЭП при работе в условиях различных карьеров и выдачу аргументированных рекомендаций. Последние охватывают мероприятия по наиболее рациональному использованию агрегатов системы, обеспечивающему заданную производительность в данных конкретных условиях при соответствующем уровне надежности тягового электрооборудования, а также определение путей совершенствования электрооборудования СТЭП с целью расширения сферы эффективного применения карьерных автомобилей.
Основными задачами исследования системы тягового электропривода является:
– расчетная оценка работоспособности СТЭП карьерного автомобиля в условиях различных карьеров горнодобывающей промышленности Центрального Казахстана;
– разработка рекомендаций по наиболее рациональному использованию существующей СТЭП, а также по дальнейшему совершенствованию тягового электрооборудования карьерного автомобиля.
С целью решения задач исследования разработана методика предусматривающая: – выбор критериев оценки параметров системы тягового электропривода, обеспечивающих заданные эксплуатационные характеристики карьерного автомобиля;
– разработку математической модели «Карьерный автомобиль – условия и режимы движения – системы тягового привода»;
– разработку методики и программы экспериментальной проверки математической модели.
Анализ нагрузочных режимов тока и напряжения генераторов автосамосвалов грузоподьемностью 70–150 тс на карьерах Центрального Казахстана показывает, что в некоторых случаях наблюдаются значительные отклонения их величин от номинального уровня. Это отражается на температурном режиме охлаждения тягового генератора, т.е. при нарушении расчетной связи между величиной тока и расходом воздуха происходит перегрев обмотки якоря.
Многообразие эксплуатационных факторов и значительные колебания их величин относительно номинальных значений при неблагоприятном сочетании усугубляет температурные условия работы изоляции якоря генератора. Как показал анализ, в большинстве исследований изучается влияние отдельных факторов на температурное поле якоря генератора.
Это является недостаточным, т.к. в реальных условиях действует большое их многообразие. Поэтому задача сводится к отысканию условий нагрузочных параметров генератора при минимально допустимой величине температуры наиболее нагреваемой части обмотки якоря. Таким образом, исследования требуют решения экстремальной задачи, направленной на отыскание оптимальных условий протекания процессов или оптимальный выбор рабочих параметров.
Предварительно проведенные исследования позволили исключить несущественные факторы и ограничиться основными параметрами, к которым относятся: ток нагрузки генератора; скорость и вес; расход воздуха в системе вентиляции генератора; температура окружающего воздуха, в качестве выходного параметра примем максимальную температуру перегрева обмотки якоря генератора, материалы которой относятся к классу изоляции В с допустимой абсолютной температурой нагрева 120 °С.
Для описания процесса воспользуемся методами дисперсионного в регрессионного анализов, базирующихся на планировании эксперимента. Это приводит, по существу, к новому методу описания изучаемого процесса. Здесь математическим методам отводится активная роль.
По данным экспериментальной статистики по изучаемому процессу выбирается некоторая оптимальная стратегия для управления экспериментом. Задача планирования заключается в следующем: на каждом этапе исследования нужно выбрать оптимальное расположение точек в факторном пространстве для того, чтобы получить некоторое представление о поверхности отклика. Здесь приходится учитывать как постановку задачи экспериментатором, так и реальную ситуацию, в которой приходится решать ее.
Как известно, регрессионный анализ основывается на методе наименьших квадратов. Вкратце изложим суть метода [2].
Допустим, что исследуемый параметр – температура перегрева обмотки якоря – имеет определенное количество измерений в условиях эксплуатации. Кроме того, он зависит от Кi эксплуатационных факторов, которые из условий статистики независимые переменные измерения. Обозначим их через x1, х2, х3, ..., хn. Представим результаты наблюдений в виде полинома степени α. Основная задача заключается в том, чтобы по данным эксплуатационной статистики измерений определить коэффициенты регрессии из выражения Сa a+к. Количество наблюдений должно удовлетворять неравенству
N ≥ Сa a+к. (1)
Учитывая свойства регрессионного анализа, должны выполняться следующие условия:
1. Результаты наблюдений y1, y2, y3, ..., yi представляют собой независимые нормально распределенные случайные величины:
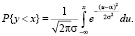 (2)
(2)
Приведенное требование не является обязательным. Метод наименьших квадратов можно рассматривать как частный случай метода максимума правдоподобия. В этом случае можно говорить о достаточных статистиках, т.е. таких функциях, которые позволяют определить информацию об исследуемых параметрах. Учитывая это, температуры якоря записывали непрерывно при помощи самопишущих приборов. Кроме того, для устойчивости результатов измерений были проведены многократные экспериментальные исследования.
2. При многократных наблюдениях над исследуемой величиной У, при некотором определенном наборе значений x1i, x2i, ..., xki получаем дисперсию s2{yi}, которая не будет зависеть от математического ожидания М{yi}, т.е. не будет отличать от дисперсии s2{yi}, полученной при повторных наблюдениях для любого другого набора значений независимых переменных x1e, x2e, ..., xke или дисперсии:
s2{yu}, u = 1, 2, …, N.
3. Независимые переменные x1e, x2e, ..., xke измеряются с пренебрежимо малой ошибкой по сравнению с ошибкой в определении У. Из большого количества эксплуатационных факторов были выбраны определяющие: вес в скорость движения, так и расход воздуха системы вентиляции генератора, температура окружающего воздуха [2].
Остальные факторы в условии задачи не учитываются как несущественные.
Для определения коэффициента регрессии введем новую переменную, тогда в новой системе обозначения полинома в степени будет записываться как однородные линейное уравнение вида
Y = b0x0 + b1x1 + … + bkxk, (3)
где К = Сaк+a-1
Из всех полиномов степени a ос отыскиваем тот, который минимизирует сумму квадратов отклонений:
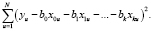 (4)
(4)
Решая систему полученных нормальных уравнений относительно неизвестных коэффициентов регрессии, определяем значения:
b0(00)+b1(01)+…+bk(0k) = (0y),
b0(10) + b1(11) +…+ bk(1k) = (1y), (5)
-------------------------------------
b0(k0) + b1(k1) +…+ bk(kk) = (ky),
где введены обозначения:
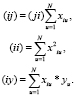 (6)
(6)
Для упрощения решения системы уравнений (5) применяем матричную форму планирования, соблюдая следующие условия:
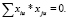 (7)
(7)
где – i ≠ j т.е. скалярные произведения всех вектор-столбцов равны нулю. Тогда при «ортогональном» планировании матрица коэффициентов нормальных уравнений станет диагональной, и коэффициенты регрессии определятся по формуле
bi = Cii(iy), (8)
где 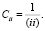
Вычислив коэффициенты регрессии, необходимо произвести статистический анализ уравнения, которое предусматривает определенный разброс значений функции относительно исходных величин [4]. Для определения дисперсии, характеризующей рассеяние остаточных точек, воспользуемся матричным уравнением
Y = XB,
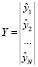 ,
,
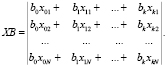 (9)
(9)
Для остаточной суммы квадратов имеем
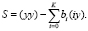 (10)
(10)
Разделив (10) на число степеней свободы, получим остаточную дисперсию:
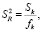 (11)
(11)
где fk = N – K – 1.
Гипотезу об адекватности представления результатов полиномом заданной степени a определяем F отношением:
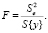 (12)
(12)
Предлагается метод нахождения ошибки опыта. Для этого необходимо знать функцию плотности величины:
y = f(x1, x2, …, xk).
Пусть f(x1, x2, …, xk) – априорная функция плотности.
Тогда математическое ожидание будет равно
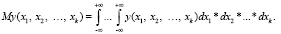 (13)
(13)
Исходя из этого
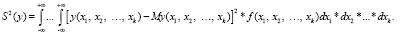 (14)
(14)
В некоторых случаях при решении практических задач сбор статистики производят, фиксируя исследуемые параметры. В результате выходные параметры принимают значения y1, y2, ..., yk.
Тогда величина S2(y) определяется по формуле
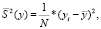 (15)
(15)
где 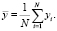
Матрица планирования экспериментов
|
№ п/п |
x0 |
X1 |
X2 |
X3 |
X1x2 |
X1x3 |
X2x3 |
X1x2x3 |
|
|
1 |
+ |
– |
– |
– |
J |
+ |
+ |
+ |
– |
|
2 |
+ |
+ |
– |
– |
a |
– |
– |
+ |
+ |
|
3 |
+ |
– |
+ |
– |
b |
– |
+ |
– |
+ |
|
4 |
+ |
– |
– |
+ |
c |
+ |
– |
– |
+ |
|
5 |
+ |
+ |
+ |
– |
ab |
+ |
– |
– |
– |
|
6 |
+ |
+ |
– |
+ |
ac |
– |
+ |
– |
– |
|
7 |
+ |
– |
+ |
+ |
bc |
– |
– |
+ |
– |
|
8 |
+ |
+ |
+ |
+ |
abc |
+ |
+ |
+ |
+ |
|
В0 = 133,1 |
В1 = 3,6 |
В2 = 3,6 |
В3 = – 2,37 |
В4 = – 11,2 |
В5 = – 0,87 |
В6 = 0,125 |
В7 = – 0,63 |
Для описания критической области эксплуатационных факторов были приняты основные из них, существенно влияющие на работу генератора, приводящие к перегреву изоляции обмотки якоря [3]:
К ним относятся:
x1 – ток нагрузки генератора, а;
x2 – температура окружающего воздуха, °С;
x3 – расход воздуха системы вентиляции генератора, м3 /сек.
Рассматривается трехфакторный эксперимент, тогда количество проделанных экспериментов N = 23 = 8.
Результаты экспериментов сведены в матрицу планирования (таблица), в которой даны кодовые обозначения независимых переменных и их сочетания.
Так как в данной задаче исследуется критическая область, то необходимо установить определенные уровни факторов, а также интервалы варьирования с учетом допустимой температуры нагрева изоляции обмотки якоря (120 °С).
Для упрощения расчета таблицы методикой предусматривается переход от натуральных переменных к кодовым по формуле
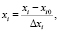 (16)
(16)
где xi – произвольное значение независимого переменного;
xi0 – значение независимого переменного, соответствующего основному уровню;
Δxi – единица варьирования независимого переменного.
По данным опыта получены численные значения коэффициентов регрессий (таблица) b1, b2, ..., b7.
Уравнение регрессий 17 для расчета температуры нагрева обмотки якоря:
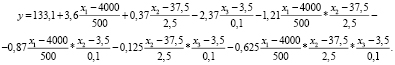 (17)
(17)
Подставляя значения пределов варьирования в уравнение (17), находим функцию отклика, т.е. температуру нагрева обмотки якоря от действия эксплуатационных факторов: тока нагрузки x1, расхода воздуха в системе вентиляции x2 и температуры окружающего воздуха x3.
Для проверки воспроизводимости экспериментальных данных по формуле вида
y = b0 + b1x1 + b2x2 + b3x3 + b4x1x2 + + b5x1x3 + b6x2x3 + b7x1x2x3 (18)
были пересчитаны их значения. В результате установлена достаточная воспроизводимость экспериментальных данных.
Выводы
Полученная формула (18) позволяет определить температуру наиболее нагреваемой части обмотки якоря при различных вариантах влияния эксплуатационных факторов.
Библиографическая ссылка
Алиев Ж.А., Жумабеков А.Т., Аскаров Б.Ш., Жаркенов Н.Б., Есбосынов К.Т. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВЛИЯНИЯ ЭКСПЛУАТАЦИОННЫХ ФАКТОРОВ НА НАГРЕВ ОБМОТКИ ЯКОРЯ ТЯГОВОГО ГЕНЕРАТОРА КАРЬЕРНЫХ АВТОСАМОСВАЛОВ // Международный журнал прикладных и фундаментальных исследований. 2017. № 8-1. С. 7-11;URL: https://applied-research.ru/ru/article/view?id=11749 (дата обращения: 11.02.2026).

