Результаты ряда теоретических и экспериментальных исследований [1–17] обусловили заметный прогресс в выявлении и понимании особенностей динамики гидромеханических систем, закономерностей силового взаимодействия и совместного движения жидкостей и контактирующих с ними твердых и газовых тел (стенок, включений) в различных гидромеханических условиях. Данная научная область неизменно актуальна. Исследования осуществляются на основе теоретических задач в точных постановках и направленных экспериментов с определением факторов, принципиальным образом влияющих на наблюдаемые результаты. К настоящему времени, в частности, является установленным, что гидромеханические системы могут проявлять заданные свойства, демонстрировать необычное и даже парадоксальное поведение; обнаружены новые гидромеханические эффекты.
Область исследований, теоретические и экспериментальные результаты
В работе [1] рассмотрена следующая задача, постановка и изучение которой в значительной мере предопределили содержание дальнейших исследований. В идеальной жидкости, ограниченной извне плоской поверхностью твердой стенки, находится твердое тело (круговой цилиндр). В начальный момент времени стенка, жидкость и тело неподвижны. В последующие моменты времени стенка, вибратор совершает заданные периодические поступательные колебания вдоль оси, нормальной к ее границе. Требуется определить движение тела, включения. Реализовано приближение малых значений отношения радиуса тела к расстоянию между телом и стенкой. Доказано, что для ρв ≠ ρж (ρв, ρж – плотности соответственно включения и жидкости) на каждую часть единичной длины включения со стороны жидкости действует направленная к стенке сила, модуль которой неограниченно возрастает с ростом характерной скорости стенки. Таким образом, включение притягивается к стенке, и это притяжение может быть достаточным для того, чтобы скомпенсировать или даже превысить иные возможные силовые воздействия на включение. Данный результат свидетельствует о наличии следующих эффектов необычного, парадоксального движения твердого тела в колеблющейся (вибрирующей) жидкости. В присутствии силы тяжести (при ускорении свободного падения, отличном от нуля: g ≠ 0) – на фоне колебаний – тело, более плотное, чем жидкость, находясь над стенкой, тонет быстрее; находясь под стенкой, тонет медленнее, всплывает вместо того, чтобы тонуть, не тонет и не всплывает – «левитирует»; тело, менее плотное, чем жидкость, находясь под стенкой, всплывает быстрее; находясь над стенкой, всплывает медленнее, тонет вместо того, чтобы всплывать, не всплывает и не тонет – «левитирует». Если сила тяжести отсутствует, g = 0, и ρв ≠ ρж, то и при ρв > ρж, и при ρв < ρж, включение (на фоне колебаний) движется к стенке, к вибратору.
Работа [1] по существу явилась истоком актуального научного направления – изучения динамики гидромеханических систем при периодических воздействиях (см. в связи с этим также [18–20]). Данное направление, в частности, непосредственно связано с проблемой выявления новых возможностей управления гидромеханическими системами.
Исследование, отраженное в [1], нашло свое развитие в [3].
В работе [2] получены результаты, отличные от представленного выше для g = 0 на качественном уровне. Рассмотрена следующая задача. В идеальной не ограниченной извне жидкости находятся два твердых тела (шары). В начальный момент времени жидкость и оба тела неподвижны. В последующие моменты времени первое тело, вибратор, совершает заданные периодические поступательные колебания вдоль оси, произвольным образом ориентированной в пространстве. Требуется определить движение второго тела, включения. Найдено решение задачи для малых значений отношения радиуса первого тела к расстоянию между телами (радиус второго тела не мал и не велик по сравнению с радиусом первого тела). Установлено, что второе тело, включение ведет себя по-разному в зависимости от того, как соотносится его плотность с плотностью жидкости: включение, плотность которого больше, чем плотность жидкости (ρв > ρж), движется к вибратору, к первому телу; включение, плотность которого меньше, чем плотность жидкости (ρв < ρж), движется от вибратора. Второе тело, плотность которого совпадает с плотностью жидкости, в реализованном в [2] приближении (на фоне колебаний) пребывает в состоянии покоя.
Интересно отметить, что в [2] колеблющееся первое тело может рассматриваться как «источник гравитации»: второе тело, плотность которого больше, чем плотность жидкости, «тонет», второе тело, плотность которого меньше, чем плотность жидкости, «всплывает».
Анализ результатов, полученных в [1, 2], привел к началу содержательной классификации колебаний жидкости, к разделению колебаний жидкости на однородные и неоднородные [8]. Пусть включения в жидкости (движение которых изучается) отсутствуют; тогда колебания жидкости являются однородными, если все частицы жидкости движутся с одной и той же скоростью, колебания жидкости являются неоднородными, если не все частицы жидкости движутся с одной и той же скоростью. Колебания жидкости, в частности, в [1, 3] являются однородными, в [2] – неоднородными.
Важное место в исследованиях необычного, парадоксального поведения включений в колеблющейся жидкости принадлежит установлению и использованию принципа, состоящего в том, что в основе содержательных различий между движением включений в жидкости при наличии колебательных воздействий и в отсутствие колебательных воздействий на гидромеханическую систему находится возможность совершения включениями движения в различных направлениях в неодинаковых условиях (см., в частности, [10]).
В работе [4] поставлена и решена задача о движении газового включения, пузыря в колеблющейся вязкой жидкости как задача о течении жидкости со свободной границей. Обнаружен эффект преимущественно однонаправленного движения газового пузыря в колеблющейся (вибрирующей) жидкости. Сущность данного эффекта состоит в том, что газовый пузырь в жидкости, заполняющей (вместе с пузырем) замкнутый сосуд, вследствие заданных колебаний и деформаций сосуда перемещается в заданном направлении. В [6] представлены экспериментальные данные, подтверждающие наличие этого эффекта. Работа [7] посвящена экспериментальному обнаружению эффекта преимущественно однонаправленного движения сжимаемого твердого тела в колеблющейся жидкости (аналогичного эффекту преимущественно однонаправленного движения газового пузыря). В [11] проведено математическое моделирование данного эффекта, поставлена и решена задача о движении пульсирующего твердого тела (шара) в колеблющейся вязкой жидкости (достигнуто соответствие между теорией и экспериментом). Таким образом, исследования, отраженные в [4, 6, 7, 11], привели к установлению существования явления преимущественно однонаправленного движения сжимаемых включений в колеблющейся (вибрирующей) жидкости. Представленными результатами, в частности, были обусловлены изобретения – способа очистки жидкости от частиц (Патент РФ № 2023772) и устройства для очистки жидкости от частиц (Патент РФ № 2103045).
Как известно [5], многие тела (организмы, устройства) могут совершать самодвижение в жидкости, т. е., находясь в жидкости, перемещаться, отталкиваясь от нее. В работе [5] получены уравнения и сформулирована концепция самодвижения твердого тела в жидкости. Поставлена и изучена задача о движении в покоящейся на бесконечности вязкой жидкости самодвижущегося тела с периодически по времени работающим движителем. В частности, определено асимптотическое поведение скорости жидкости на больших расстояниях от самодвижущегося тела. (В связи с проблемой самодвижения см. также [21–24]).
Интересно отметить, что решенная в [5] задача может служить математической моделью самодвижения в жидкости микроорганизма Paramecium (класс ресничных инфузорий) [25, 26].
Одним из актуальных направлений в гидромеханике является изучение термокапиллярной конвекции жидкости в плавающей области, жидком мостике. Данное направление имеет непосредственное отношение к проблеме создания высококачественных материалов. Задачи, касающиеся этого направления, весьма сложны ввиду того, что жидкость (расплав), образуя собой жидкий мостик, соприкасается с двумя твердыми телами и с газом; граница плавающей области частично является твердой, а частично – свободной. В работе [9] предложен подход, позволяющий осуществлять эффективное аналитическое изучение термокапиллярной конвекции в плавающей области. Данный подход может использоваться при математическом моделировании как стационарных, так и нестационарных пространственных течений жидкости в плавающей области как в отсутствие, так и при наличии массовых сил. (В связи с проблемой создания высококачественных материалов см. также [27–30]).
Среди наиболее интригующих, опасных и еще не вполне изученных явлений Природы достойное место занимает смерч, торнадо. Важнейшая особенность этого явления – громадная скорость ветра, скорость вращения стенок воронки смерча, достигающая 50–300 м/с и больше; внутренность воронки наполнена относительно слабо движущимся разреженным воздухом, давление в ней понижено на величину порядка 85 мбар [31–33]. В работе [12] построена математическая модель смерча, естественным образом соединяющая основные характерные черты этого явления, приводящая к результатам, количественно согласующимся с данными наблюдений. В частности, моделью демонстрируется непосредственная связь смерча со смерчевым облаком; теоретически найденные значения скорости ветра и понижения давления воздуха в смерче составляют соответственно 150 м/с и 110 мбар. (В связи с проблемой торнадо см. также [34–40].)
Классификация колебаний жидкости, произведенная в [8], получила свое развитие в [13]. В этой работе введены количественные характеристики неоднородности колебаний жидкости: определены коэффициент неоднородности колебаний жидкости в точке и средний коэффициент неоднородности колебаний жидкости по области. Установлено, в частности, что движение включения в однородно и неоднородно колеблющейся жидкости может быть различным на качественном уровне, сколь бы слабой ни была неоднородность колебаний жидкости.
В работах [14, 15] рассмотрены задачи о колебаниях в идеальной жидкости неоднородного твердого тела в присутствии силы тяжести, при наличии или в отсутствие вибрационных воздействий на гидромеханическую систему. Обнаружены эффекты положения равновесия и циклической частоты колебаний твердого тела в жидкости. Найдено, что тело в жидкости может находиться в состоянии движения, аналогичном маятнику Капицы [41, 42], т.е. совершать движение «в перевернутом виде», совершать парадоксальные, «перевернутые» колебания. Установлено, что в присутствии вибрационных воздействий тело в жидкости может выходить из состояния безразличного равновесия, приобретать положения устойчивого равновесия, совершать колебания, период которых отличен от периода воздействий на гидромеханическую систему.
Задачи, касающиеся динамики вязкой жидкости, как правило, характеризуются повышенным уровнем сложности [43–46]. К существенным дополнительным затруднениям в их изучении приводит наличие парадокса Стокса. Данный парадокс состоит в том, что плоская задача о течении не ограниченной извне покоящейся на бесконечности вязкой жидкости вокруг цилиндрического твердого тела, движущегося в ней с постоянной скоростью под действием внешних сил, при малых значениях числа Рейнольдса (при малой скорости тела, при малом характерном размере тела, при большой вязкости жидкости) не имеет решения [47–50]. В частности, в связи с этим в работе [16] рассмотрена следующая задача. В вязкой не ограниченной извне жидкости находится сжимаемое твердое тело (круговой цилиндр). Радиус тела и скорость жидкости на бесконечности периодически с периодом T изменяются со временем; среднее по времени значение скорости жидкости на бесконечности равно нулю. Тело подвергается внешнему стационарному силовому воздействию. Требуется определить движение тела и жидкости. Реализовано приближение малых значений параметров ε = QT / A0 и ℵ = δA / A0 (Q – наибольшее значение модуля скорости жидкости на бесконечности; δA – наибольшее значение |A – A0|; A – радиус тела; A0 – значение радиуса A в отсутствие его изменений со временем). Обнаружено, в частности, наличие разрешенных и запрещенных состояний гидромеханической системы (наличие разрешенных и запрещенных пульсаций тела, колебаний жидкости на бесконечности и внешнего силового воздействия), для которых нетривиальное решение задачи о среднем по времени движении тела соответственно существует и не существует (найден критерий существования решения данной задачи). Показано, что в разрешенных состояниях гидромеханической системы, в стационарной составляющей задачи о течении жидкости вокруг тела числом Рейнольдса является величина Re = εℵA02 / (νT) (ν – кинематический коэффициент вязкости жидкости). Таким образом, для ε → 0, ℵ → 0 имеет место стационарное обтекание цилиндрического твердого тела плоским потоком вязкой жидкости при малых значениях числа Рейнольдса Re. При этом парадокс Стокса отсутствует.
Изучение движения гидромеханических систем, состоящих из вязкой жидкости и двух твердых стенок, в течение длительного времени сохраняет актуальность (см. [51–58]). Характерным для задач, касающихся данного объекта исследований, является то, что стенки испытывают внешние силовые воздействия, покоятся либо совершают заданное движение. В работе [17] поставлена и решена задача, в которой гидромеханическая система также подвергается внешним силовым воздействиям, вследствие чего одна из стенок является закрепленной, покоится. Однако на другую – свободную – стенку действуют лишь внутренние силы; совместное затухающее движение свободной стенки и жидкости подлежит определению. Получена формула для характерного времени торможения свободной стенки. Определено условие, при выполнении которого происходит резкое торможение гидромеханической системы.
Постановка и решение задачи
Рассмотрим следующую задачу. В идеальной несжимаемой не ограниченной извне жидкости находится сжимаемое твердое тело, шар. Центр тела совпадает с точкой ξ, началом инерциальной прямоугольной системы координат x, y, z. Жидкость подвергается воздействиям со стороны тела, радиус a которого заданным образом изменяется со временем t, и воздействиям, проявляющимся в том, что жидкость на бесконечности движется с заданной, зависящей от времени скоростью v∞:
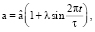
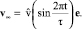 (1)
(1)
Здесь 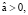
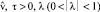 – параметры; e = {0, 0, 1}. Оказываемые на жидкость воздействия вызывают ее движение в области ω: r > a
– параметры; e = {0, 0, 1}. Оказываемые на жидкость воздействия вызывают ее движение в области ω: r > a  Данное движение требуется определить. Постановку задачи составляют уравнение неразрывности и условия на границе тела и на бесконечности:
Данное движение требуется определить. Постановку задачи составляют уравнение неразрывности и условия на границе тела и на бесконечности:
Δφ = 0 в ω, (2)
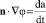 при r = a, (3)
при r = a, (3)
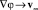 при r →∞, (4)
при r →∞, (4)
где φ – потенциал скорости жидкости; n – единичный вектор внешней нормали к сфере r = a. Задача (2)–(4) имеет решение:
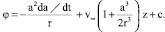 (5)
(5)
Здесь v∞ = v∞•e; c – функция t.
Из (1), (5) следует, что (в области r > (1 + |λ|)  ) скорость жидкости
) скорость жидкости 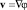 может быть представлена в виде
может быть представлена в виде
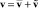 , (6)
, (6)
где
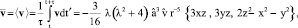 (7)
(7)
– средняя скорость жидкости; 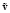 – колебательная скорость жидкости
– колебательная скорость жидкости 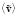 = 0).
= 0).
Согласно (1), (3), (4), жидкость подвергается периодическим по времени воздействиям, которые характеризуются, в частности, соотношениями da/dt = 0, 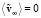 . Область ω, при всех значениях t, симметрична относительно точки ξ и плоскости z = 0. Воздействия на жидкость, выражаемые формулой (3), симметричны относительно точки ξ, изменения со временем скорости (da/dt)n одинаковы для направлений, совпадающих с направлениями векторов n и – n; воздействия на жидкость, выражаемые формулой (4), не зависят от знака z, изменения со временем скорости v∞ одинаковы для направлений, совпадающих с направлениями векторов e и – e. Ввиду изложенного, в отношении воздействий, испытываемых жидкостью, на оси z имеет место равноправие двух направлений, совпадающих с направлениями векторов e и – e; отсутствует преимущественное, выделенное направление. Тем не менее, согласно (6), жидкость, колеблясь, совершает среднее по времени, стационарное движение, которое на оси z происходит лишь в одном направлении. Из (7) следует, что данным – единственным реализующимся – направлением является: совпадающее с направлением вектора e, если
. Область ω, при всех значениях t, симметрична относительно точки ξ и плоскости z = 0. Воздействия на жидкость, выражаемые формулой (3), симметричны относительно точки ξ, изменения со временем скорости (da/dt)n одинаковы для направлений, совпадающих с направлениями векторов n и – n; воздействия на жидкость, выражаемые формулой (4), не зависят от знака z, изменения со временем скорости v∞ одинаковы для направлений, совпадающих с направлениями векторов e и – e. Ввиду изложенного, в отношении воздействий, испытываемых жидкостью, на оси z имеет место равноправие двух направлений, совпадающих с направлениями векторов e и – e; отсутствует преимущественное, выделенное направление. Тем не менее, согласно (6), жидкость, колеблясь, совершает среднее по времени, стационарное движение, которое на оси z происходит лишь в одном направлении. Из (7) следует, что данным – единственным реализующимся – направлением является: совпадающее с направлением вектора e, если 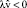 , совпадающее с направлением вектора – e, если
, совпадающее с направлением вектора – e, если 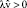 . Таким образом, имеет место парадоксальное движение жидкости: испытывая «неоднонаправленные», равноправные, симметричные, периодические по времени воздействия, жидкость, на фоне колебаний, производит «однонаправленную» реакцию – стационарное движение в одном, преимущественном, выделенном направлении.
. Таким образом, имеет место парадоксальное движение жидкости: испытывая «неоднонаправленные», равноправные, симметричные, периодические по времени воздействия, жидкость, на фоне колебаний, производит «однонаправленную» реакцию – стационарное движение в одном, преимущественном, выделенном направлении.
Заключение
Представленные работы, полученные теоретические и экспериментальные результаты свидетельствуют о значимости и перспективности исследований в рассмотренной области, демонстрируют наличие содержательной связи этих исследований с широким спектром проблем фундаментального и прикладного характера.
Библиографическая ссылка
Сенницкий В.Л. ПАРАДОКСАЛЬНОЕ ДВИЖЕНИЕ ЖИДКОСТИ // Международный журнал прикладных и фундаментальных исследований. 2017. № 8-1. С. 28-33;URL: https://applied-research.ru/ru/article/view?id=11753 (дата обращения: 11.02.2026).
DOI: https://doi.org/10.17513/mjpfi.11753

