Регистрация и выхаживание детей с экстремально низкой массой тела (от 500 г) началась в 2012 г. в соответствии с Приказом МЗ и СР РФ от 27.12.2011 г. № 1687н. В связи с этим становится актуальным использование современных интеллектуальных систем и систем поддержки принятия решений в области медицинской диагностики и прогнозирования не только для снижения перинатальной и младенческой смертности, но и улучшения качества прогноза их дальнейшего развития.
Среди множества задач в области здравоохранения, которые могут быть решены с помощью информационных систем, можно выделить последовательность «диагностика – прогнозирование – лечение» [1].
Неточности в диагностике и прогнозировании могут привести к ошибочному лечению, что может нанести вред больному. Зачастую врач в процессе диагностики принимает решение в условиях неопределенности, опираясь на личный опыт и знания. Поэтому усилия многих специалистов в области информационных технологий направлены на проектирование систем, имитирующих эвристики врача, или попытки алгоритмизировать процесс принятия решения в медицине, основываясь на знаниях экспертов [2].
На сегодняшний день остаются актуальными вопросы, связанные с повышением эффективности процесса принятия решений при диагностике и прогнозировании, заключающиеся в повышении уровня оперативности, достоверности и обоснованности получаемых назначений.
Степень изученности
Вопросами применения интеллектуальных систем в медицине занимаются множество ученых по всему миру: P.Y. Аncel, N. Lelong, E. Papiernik [2], L.K. Smith, E.S. Draper, B.N. Mankletow [3], Greg Kochanski и т.д.
Вопросам компьютерной диагностики и прогнозирования состояния здоровья детей с ЭНМТ посвящены работы В.Ю. Альбицкого, Е.Н. Байбариной [8], А.А. Баранова, Н.В. Башмаковой, А.Н. Большаковой, И.В. Виноградовой, В.В. Ковалева, И.В. Колмакова, С.С. Смирновой, З.Х. Сорокиной, Т.Н. Углевой, О.Г. Фроловой, Е.Д. Хадиевой, М.П. Шуваловой, А.Н. Юсуповой.
Математическая постановка задачи
Каждый класс описывается n признаками, которые представляют собой набор показателей.
Имеется вектор X (x1,x2, …, xn), где xi – показатели, характеризующие функциональное состояние организма ребенка, n – количество учитываемых показателей.
Состояние каждого ребенка относится к одному из 2-х непересекающихся классов m = 2 (исходов):
– болезнь;
– выздоровление.
Исследования проводились по 16 показателям, измеренным у матери в 1, 2 и 3 триместрах беременности и у детей на 1, 7, 30 сутки жизни ребенка.
Требуется по имеющимся показателям дать оценку функциональному состоянию организма ребенка.
Выбор программного обеспечения
В работе для генерации нейронных сетей используется нейроимитатор Neural Network Toolbox MatLab.
MatLab, разработка компании компанией Math Works – прикладная программа для решения вычислительных задач и язык программирования, используемый в этом пакете.
Пакет Neural Networks Toolbox Matlab – это полноценная среда, предназначенная для решения прикладных задач с использованием нейронных сетей. Toolbox NNT Matlab может использоваться для решения множества разнообразных задач: обработка сигналов, нелинейное управление, финансовое моделирование и т.п.
Нейросетевые технологии в оценке состояния здоровья новорожденных детей
Искусственные нейронные сети (ИНС) – это вычислительные структуры, моделирующие биологические процессы, которые связаны с процессами, протекающими в человеческом мозге. Это системы, которые способны обучаться посредством анализа положительных и отрицательных воздействий. Элементарной частицей ИНС является искусственный нейрон (просто нейрон), который был назван так по аналогии с биологическим нейроном [4].
Использование ИНС особенно эффективно при решении слабоформализованных задач, таких как распознавание образов, классификации, категоризации и других [5].
В процессе длительного естественного отбора биологические системы получили эффективные механизмы функционирования. Поэтому при построении многих искусственных систем в науке, технике и медицине пытаются применять эти механизмы.
Нейронная сеть, как и природный аналог, состоит из базовых элементов нейронов, которые в свою очередь включают в себя: нелинейную функцию активации; дендриты или каналы передачи информации другим нейронам; весовые коэффициенты. Принцип работы нейрона можно описать следующей парой уравнений [5]:
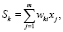 (1)
(1)
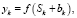 (2)
(2)
где x1, x2,…, xm – входные сигналы;
wk1,wk2,…,wkm – синаптические веса k-го нейрона;
Sk – линейная комбинация входных сигналов;
bk – порог;
f( ) – функция активации;
yk – выходной сигнал нейрона.
Модель нейрона представлена на рисунке.
Следовательно, базовый принцип работы сети следующий: вычисляем скалярное произведение вектора весовых коэффициентов и входного вектора, генерируем выходной сигнал нейрона, зависящий от типа активационной функции, принимающей в качестве аргумента скалярное произведение.
Существует несколько видов активационных функций [4]:
1. Единичный скачок или жесткая пороговая функция. Значение единичной функции активации равно 1, если входное значение больше порогового, иначе – 0.
2. Линейный порог или гистерезис. Гистерезис имеет два линейных участка, на которых активационная функция тождественно равна 0 и 1, и участок строго монотонного возрастания функции.
3. Гиперболический тангенс. Гиперболический тангенс (S-образная функция) имеет симметрию относительно начала координат. Выходной сигнал f(S) в точке S = 0 имеет значение равное нулю. Способность гиперболического тангенса принимать значения различных знаков применяется для целого ряда нейросетей.
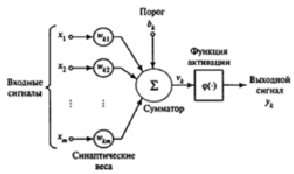
Модель нейрона
4. Сигмоидальная функция. Как и гиперболический тангенс, является S-образной функцией. Принимает значения в пределах [0; 1]. Сигмоидальная функция имеет простую производную и дифференцируема на всей оси абсцисс, что является ее основным достоинством.
Функции активации типа гистерезиса и единичного скачка редко встречаются на практике. На практике почти всегда применяется сигмоидальная активационная функция.
К настоящему времени изучено достаточно большое количество моделей нейронных сетей. Сети бывают 2-х видов: однослойные, многослойные [4].
Несмотря на то, что один нейрон может выполнить самые простые процедуры распознавания, для решения сложных задач нейроны необходимо объединить в сети. Самая простая сеть состоит из одного слоя нейронов. Информация от входного слоя передается на выходной. Такая сеть называется однослойной.
Для решения более сложных задач используются более крупные и сложные нейронные сети, состоящие из нескольких слоев нейронов. Данные сети обладают большими вычислительными возможностями. В таких сетях нейроны объединяются в слои, содержащие нейроны с едиными входными сигналами. В общем случае нейронная сеть содержит несколько слоев. В многослойной сети кроме входного и выходного слоев могут быть один или несколько скрытых слоев [5].
Многослойные сети принято делить на [6, 7]:
- Сети без обратных связей или сети прямого распространения.
- Сети с обратными связями или рекуррентные сети.
Одной из основных задач при использовании нейронных сетей является подбор весовых коэффициентов для решения рассматриваемой задачи. Для этой цели существуют правила обучения нейронных сетей (алгоритмы), которые определяют, как изменяются значения весовых коэффициентов в зависимости от входных сигналов.
Алгоритмы обучения бывают 2-х видов [4].
- Обучение с учителем.
Обучение с учителем ИНС заключается в том, что сеть обучается на одном множестве данных, а проверяется на другом. Таким образом, обучение многослойной ИНС можно представить двумя этапами [5]:
Предъявление НС обучающего множества до тех пор, пока либо ошибка сети не станет меньше заданной, либо по истечении заданного числа эпох.
Проверка правильности на тестовом множестве. Если ошибка обобщения больше заданной, то производится либо увеличение числа эпох, либо числа обучающих примеров, либо изменения архитектуры ИНС.
- Обучение без учителя.
Обучение без учителя не требует сравнения с известными заранее идеальными ответами. Обучающее множество состоит только из входных векторов. Алгоритм обучения без учителя настраивает веса сети таким образом, чтобы получались согласованные выходные векторы, т.е. предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения группирует сходные векторы в классы. Входной сигнал из данного класса формирует определенный выходной сигнал, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных сигналов. Следовательно, выходы такой нейронной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения [7].
Часто при обучении многослойных нейронных сетей используют алгоритм обратного распространения ошибки, относящийся к алгоритму обучения с учителем. Обучение этим алгоритмом предполагает два прохода по всем слоям сети: прямого и обратного. Во время прямого прохода входной вектор подается на входной слой нейронной сети, после чего распространяется по слоям сети. В результате генерируется набор выходных сигналов, являющийся фактической реакцией сети на данный входной сигнал. При прямом проходе все веса сети фиксированы. Для обратного прохода веса нейросети настраиваются в соответствии с правилом коррекции ошибок, а именно: фактический выход сети вычитается из желаемого, в результате чего формируется сигнал ошибки. Этот сигнал впоследствии распространяется по сети в направлении, обратном направлению синаптических связей.
Однако обратное распространение несет в себе определенные проблемы. Во-первых, нет гарантии, что сеть обучится за конечное время. Иногда усилия, потраченные на обучение сети, пропадают напрасно после затрат большого количества времени. Во-вторых, нет уверенности, что сеть обучится наилучшим образом. Алгоритм обучения может попасть в точку локального минимума, в результате чего может быть получено худшее решение [7].
Искусственные нейронные сети предложены для решения множества задач. Как и большинство математических методов, нейронные сети позволяют лишь с некоторой вероятностью давать ответ на поставленный вопрос. В области медицины этот подход дает дополнительную информацию для постановки диагноза врачу.
Анализ результатов
По результатам обследования 46 детей формируется выборка, которая разделена на 2 класса (диагноза): здоровые (30 ребенок) и больные (16 ребенок).
В процессе исследования построена нейронная сеть, результатом которой является отнесение объекта к одному из классов (болен, здоров).
Задача заключалась в обучении нейронной сети с 16 входами, представляющими собой медицинские показатели, и 1 выходом, который определяет диагноз. Данная задача относится к классу задач классификации, т.е. необходимо определить значение (0 или 1) выхода нейронной сети относительно каждого набора входных данных.
Исходная выборка была разбита на 2 группы: обучающая (31 ребенок) и тестируемая (15 детей).
В настоящее время не существует точных критериев выбора модели нейронной сети, данный выбор основан на опыте исследователей и зависит непосредственно от решаемой задачи. Проанализировав результаты работ ряда авторов [4–6], принято решение остановиться на модели трехслойной сети. В качестве обучающего алгоритма выбран алгоритм обратного распространения ошибки, поскольку, обладая таким достоинством, как быстрое вычисление градиента функции ошибки, используемого для выбора направления коррекции весов, данный алгоритм реализует вычислительно эффективный метод обучения многослойной нейронной сети. Данный тип сети часто используется для решения задач классификации с помощью нейронной сети.
В качестве функции активации использована сигмоидальная функция. Данная функция удовлетворяет основному требованию алгоритма обратного распространения ошибки: имея достаточно простую производную, функция всюду дифференцируема. Кроме этого, достоинством данной функции активации является способность усиливать слабые сигналы лучше, чем большие, и сопротивляться «насыщению» от мощных воздействий [5].
Недостаточное количество нейронов в скрытом слое может привести к недообучению нейронной сети, а избыточное количество нейронов будет способствовать увеличению времени обучения сети. Для проведения исследования было принято, использовать 10 нейронов в скрытом слое.
Таким образом, структура сети имеет следующий вид: 16 нейронов во входном слое и 1 – в выходном и 10 нейронов в скрытом слое.
После подбора параметров нейронной сети проведено ее обучение.
Точность нейронной сети составляет 91,1 %. Следовательно, ошибка нейронной сети составляет 8,9 %. Практически нулевая ошибка достигается за 15 циклов обучения, средняя квадратическая ошибка тестовой выборки составляет 0,04, что соответствует ожидаемому результату.
Достоверность полученных результатов значительно повышается, т.к. точность постановки правильного диагноза экспертом составляет 89 % [3]. Полученные данные на основе исследуемых показателей дают возможность оперативно оценить функциональное состояние ребенка и скорректировать программу лечения.
Заключение
Рождение здорового поколения является важной составляющей успеха всей нации в целом. Именно поэтому важное место в оценке состояния ребенка играет дородовая диагностика, адаптация и развитие организма в раннем неонатальном периоде. Организм ребенка рассматривается с позиции системного подхода как некоторая сложная динамическая самоорганизующаяся система, взаимодействующая с внешней средой и обладающая внутренними энергетическими ресурсами. Системная модель, отражающая энергоинформационные обменные процессы в организме, позволяет получить адекватные оценки состояния биосистем. Применение комплексного подхода к оценке функционального состояния организма ребенка открывает возможность выявления и профилактики не только заболеваний, но и состояний на грани нормы и патологии, что особенно актуально для детей раннего возраста, когда малейшие изменения оказывают огромное влияние на состояние здоровья новорожденных. В связи с этим сигнал о нарушении гомеостатических свойств может быть использован в диагностических и прогностических целях.
В результате исследований произведена диагностика функционального состояния здоровья детей с экстремально низкой массой тела с учетом их индивидуальных особенностей на основе математических методов.
Библиографическая ссылка
Черкашина Ю.А., Вадутова Ф.А. ОЦЕНКА СОСТОЯНИЯ ЗДОРОВЬЯ ДЕТЕЙ С ЭКСТРЕМАЛЬНО НИЗКОЙ МАССОЙ ТЕЛА НА ОСНОВЕ ТЕХНОЛОГИИ ИСКУССТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ // Международный журнал прикладных и фундаментальных исследований. 2017. № 8-1. С. 121-125;URL: https://applied-research.ru/ru/article/view?id=11772 (дата обращения: 11.02.2026).

