Объем выборки требуется определить перед началом большинства исследований. При этом тема объема выборки в медицинских исследованиях достаточно широко обсуждается в литературе [1, 3, 6–8]. Предложены различные подходы для подсчета размеров выборки в зависимости от типа и параметров исследований, а также ряд компьютерных программ для Windows и Mac (например, GPower и др.) и статистических пакетов (SPSS и т.д.). В данном сообщении представлена программа для быстрой оценки объема выборки с помощью планшетного компьютера или смартфона на базе операционной системы Андроид. Ранее мы сообщали об использовании этих популярных вычислительных средств при решении ряда других статистических задач в медицинских исследованиях [2, 4].
Целью многих статистических изысканий и тестов является сравнение двух методов лечения, лекарственных средств или групп больных. Численное значение, которое выражает интересующие исследователя различия, называется эффектом. Размер эффекта может характеризовать отношение шансов, относительный или абсолютный риск. Кроме того, весьма популярным в этой области доказательной медицины становится параметр NNT – Number need to treatment (число больных, нуждающихся в лечении) [5]. Затем, как правило, выдвигается нулевая, а также альтернативная гипотезы. По определению нулевая гипотеза постулирует, что эффекта нет (различия между результатами лечения в группах равны нулю, относительный риск равен единице), альтернативная гипотеза предполагает, что эффект есть.
Клинически важный размер эффекта – это наименьшие различия между средними значениями какой-либо изучаемой величины в группах, которые еще можно рассматривать как диагностически или клинически значимые. Наименьший клинически значимый эффект – минимальные изменения в неком показателе, которые нельзя игнорировать. Выбор его в основном лежит на исследователе, на его компетентности в сфере решаемой проблемы. Например, изучая реакцию организма пациента на физическую нагрузку, нужно определить, будет ли клинически значимым изменение частоты сердечных сокращений на 5 уд/мин или же
на 10 уд/мин, или же какое-то иное значение.
При двухстороннем тесте нулевая гипотеза заключается в отсутствии различий, а альтернативная гипотеза предполагает, что различия между группами могут идти в любом направлении. То есть при одностороннем тесте альтернативная гипотеза определяет предполагаемое направление различий.
Интерпретация результатов теста требует знания и понимания величины p-value (p-значения) – величины, применяемой при статистической проверке гипотез. Уровень значимости или p-value – это наименьшая величина уровня значимости, при которой нулевая гипотеза отвергается для данного значения статистики критерия. Другими словами, уровень значимости – это такое значение вероятности события, при котором событие уже можно считать наступившим не по случайным причинам (а в результате проведенного лечения, например).
Указание точного значения p-value является даже более информативным, чем традиционное оформление результатов проверки нулевой гипотезы в виде неравенства р < α. Напомним, что эта форма записи означает, что гипотеза была отклонена на уровне значимости α. Например, очень часто используемая запись р < 0,05 равносильна утверждению, что уровень значимости результатов наблюдений менее чем 5 %. То есть ложноположительный результат или ошибка I рода при таком уровне значимости возможны не более чем в 5 случаях из 100 (например, при таком уровне значимости мы допускаем по результатам диагностических проб ненужное лечение в действительности 5 здоровых пациентов из 100).
Уровень значимости – это пороговое значение для р-оценки, ниже которого нулевая гипотеза должна быть отвергнута и сделано заключение о том, что имеются доказательства эффекта. Обычно уровень значимости в биологии и медицине устанавливается часто по умолчанию на значении 5 %.
Мощность – это вероятность того, что нулевая гипотеза будет адекватно отвергнута, иными словами тогда, когда действительно существуют доказательства реальных различий или взаимосвязей. Ее можно рассматривать как «100 процентов минус вероятность пропуска истинного эффекта» [1]. Поэтому чем выше мощность, тем меньше вероятность пропуска истинного эффекта. Мощность обычно фиксируется на стандартном уровне 80, 90 или 95 %. Согласно большинству авторов, мощность не должна быть меньше 80 %. Если крайне важно, чтобы исследование не пропустило существующего эффекта, надо стремиться достичь мощности минимум 90 % или даже более.
В медицине мощность (чувствительность) критерия – вероятность не допустить так называемую ошибку II рода. Показатель для характеристики диагностических проб (вероятность положительного результата у больного при наличии болезни). Характеризует способность пробы выявить болезнь.
Итак, в медицинских исследованиях должна быть сформирована выборка такого размера, чтобы если подобные различия действительно существуют, то в исследовании были бы получены статистически значимые результаты.
Обсуждение расчетной формулы
Какие параметры должны учитываться при расчете объема выборки? Для отдельных дискретных величин мощности и уровней значимости необходимые размеры выборки протабулированы, а соответствующие таблицы можно найти в литературе по планированию количественных исследований [8]. Рассчитать размер выборки, необходимый для обеспечения заданной мощности t-критерия, можно также по специальным формулам, среди которых своей простотой выделяется формула Лера [7]. При сравнении двух групп для мощности 80 % и двустороннего уровня значимости 0,05 требуемый размер выборки в каждой группе равен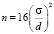 
, где σ – стандартное отклонение наблюдений по выборке, одинаковое в каждой из 2-х групп, d – оценка величины (размера) эффекта (как отмечали выше, наименьшая разность в групповых средних значениях, которая клинически значима). Кстати, научное исследование Р. Лера (1992), в котором опубликована одноименная формула, так и называется: «Sixteen S-squared over D-squared: a relation for crude sample size estimates».
Стандартное отклонение (корень из дисперсии) – это мера того, насколько сильно разбросаны опытные данные относительно их среднего значения. Анализ величины стандартного отклонения призван исключить из результатов статистического анализа ошибку «среднего значения по больнице». Из формулы видно, что чем больше разброс данных и чем меньше размер эффекта, тем больше необходимый объем выборки. Это, конечно, ожидаемый результат.
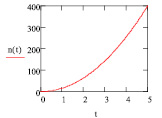
Рис. 1. Объем выборки n в зависимости от отношения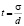 
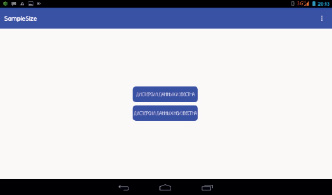
Рис. 2. Окно программы SampleSize, в котором пользователь определяет, известна дисперсия данных или нет
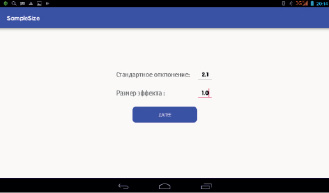
Рис. 3. Окно программы SampleSize для ввода численных значений стандартного отклонения данных и размера эффекта
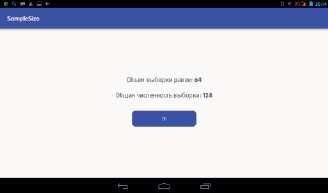
Рис. 4. Окно программы SampleSize оценки объема выборки с решением
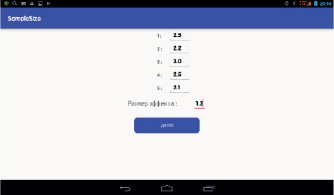
Рис. 5. Окно программы SampleSize для ввода данных пробной выборки и размера эффекта в случае, если дисперсия данных заранее не известна
Формула Лера может быть использована для построения графика (рис. 1), однако точность такого представления невысока и ценность его использования на практике в ряде случаев весьма сомнительна.
Нами данная формула была положена в основу программы, которая легко производит расчет объема выборки с известной и неизвестной дисперсией данных. Программа выполнена на базе операционной системы Android и может быть реализована с помощью планшетного компьютера или смартфона, работающих под управлением данной системы.
Алгоритм работы программы
Первоначально пользователь определяет, известно или нет стандартное отклонение (дисперсия) исследуемых данных (рис. 2). В 1-м случае в новом открывшемся окне предлагается заполнить поле для величины стандартного отклонения и поле, характеризующее размер эффекта (рис. 3). После этого программа вычисляет искомый объем выборки по формуле Лера (рис. 4). Во 2-м случае в новом окне программа запрашивает объем серии пробных измерений, затем предлагает для заполнения соответствующий массив полей для численных значений этой серии и поле для размера эффекта (рис. 5). После осуществления данных манипуляций вычисляется стандартное отклонение (не отображается) и объем выборки для данных, разброс которых исследователю заранее неизвестен. Округление числа n до целых производится по формуле n = {n} + 1, где {n} – целая часть числа n.
Таким образом, независимо от того, известно ли стандартное отклонение данных или нет, мы получаем количество больных, необходимое для включения в каждую из групп при выполнении двухвыборочного t-теста. Общая численность выборки, подлежащей исследованию, будет в два раза выше.
Библиографическая ссылка
Арутюнов С.Д., Перцов С.С., Муслов С.А. БЫСТРАЯ ОЦЕНКА ОБЪЕМА ВЫБОРКИ В МЕДИЦИНСКИХ ИССЛЕДОВАНИЯХ С ПОМОЩЬЮ АНДРОИД ПЛАНШЕТА // Международный журнал прикладных и фундаментальных исследований. – 2017. – № 8-2. – С. 198-202;URL: https://applied-research.ru/ru/article/view?id=11785 (дата обращения: 18.04.2024).