Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Дасибеков А. 1 Юнусов А.А. 2 Арапов Б.Р. 1 Куатбеков Н.А. 2 Юнусова А.А. 3 Тажбенова Г.Д. 3 Нурмаганбетова Г.К. 4

---

1 Южно-Казахстанский государственный университет им. М. Ауэзова

2 КИПУДН

3 Евразийский гуманитарный институт

4 ЮКГПИ

В глинистых грунтах деформирование под действием статической нагрузки обусловлено, главным образом, взаимным перемещением твердых частиц грунта. При этом различают объемные деформации и деформации формоизменения грунтов. Объемная сжимаемость глинистых водонасыщенных грунтов возможна лишь при отжатии воды из пор грунта. Поскольку поры грунта малы и, кроме того, часть их объема как сказано выше, занята связной водой, то отжатие свободной воды происходит медленно, и состояние деформирования грунта растягивается часто на длительный промежуток времени. Следовательно, характеристики уплотняемых грунтов есть величины переменные. В данной работе модуль деформации грунта изменяется во времени. Уравнение уплотнения решается при неоднородных граничных условиях. Определены расчетные формулы для вычисления значений порового давления p(x,t), напряжения в скелете грунта σ(x,t) и значения осадки St для любого промежутка времени от начала загружения t. При переменном во времени коэффициенте сжимаемости распределение внешней нагрузки между давлением в поровой жидкости и напряжением в скелете грунта происходит быстрее, чем при постоянной величине этого параметра, а осадок слоя грунта не меняет своего стабилизированного состояния.

Статья в формате PDF

1259 KB

процесс уплотнения

грунт

параллелепипед

давление

основание

фундамент

граничные условия

непрерывность функций

дифференциальные уравнения

гипергеометрические уравнения

1. Гольдштейн М.Н. Механические свойства грунтов. – М.: Стройиздат, 1979. – 302 с.

2. Дасибеков А.Д., Бердыбаева М.Ж. Об уплотнении грунта, модуль деформации которого изменяется по экспоненциальному закону глубины // Наука и образование Южного Казахстана. Сер. Механика и машиностроение. – Шымкент, 1999. – № 10 (17). – С. 54–60.

3. Дасибеков А.Д., Бердыбаева М.Ж., Сейткалиев А.П. О некоторых задачах механики уплотняемых сред и ее практическое применение // Наука и образование Южного Казахстана. Сер. Механика и машиностроение. – Шымкент, 2000. – С. 167–169.

4. Дасибеков А.Д., Бердыбаева М.Ж., Асибеков А., Макашева О.М. Трехмерная задача консолидации грунтов с неоднородными граничными условиями // Тр. межд. науч.-метод. конф. при университетете Дружбы народов. – Шымкент, 2006. – С. 268–271.

5. Маслов Н.Н. Основы механики грунтов и инженерной геологии. – М.: Высшая школа, 1968. – С. 265–285.

6. Терцаги К. Строительная механика грунта. – М.: Госстройиздат, 1933. – 510 с.

7. Цытович Н.А. Механика грунтов. – М.: Изд. литературы по строительству, архитектуре и строительным материалам, 1963. – 633 с.

8. Флорин В.А. Основы механики грунтов. – М.: Госстройиздат, 1959. Т.1,2. – 357 с.; 1961. – 543 с.

9. Ханходжаева Г.Ш. Расчеты консолидации упруго-ползучих водонасыщенных грунтовых оснований с учетом структурной прочности и начального градиента напора: автореф. дис. … канд. техн. наук. – Шымкент, 2010. – 20 с.

Грунты по своим структурам относятся к дисперсным системам. Промежутки между отдельными твердыми их частицами, называемые грунтовыми порами, обычно в большей или меньшей степени заполнены жидкостью (водой). Даже сухие по внешнему виду грунты содержат воду в форме тончайших пленок на поверхности минеральных частиц. Причем дисперсный грунт, в состав которого входят твердые частицы, жидкость, а иногда и газообразная среда, представляет собой многофазную систему и эта система, в зависимости от крупности частиц грунта, делится на определенные категории. При этом диапазон изменения крупности частиц грунта весьма значителен и размер частиц грунтов, которые нас интересуют, не должен превышать 0,005 мм. К этим категориям грунтов обычно относятся супесь, суглинок и глина. Они, в целом, называются глинистыми грунтами. Глинистые частицы имеют в основном, пластинчатую и игольчатую форму, что и увеличивает удельную поверхность частиц и способствует их сжимаемости. Кроме того, зная число пластичности ωn глинистых грунтов, можно определить, к какой категории он относится. При этом для супеси это число изменяется в пределах 1≤ωn ≤7, для суглинка 7≤ωn ≤17, для глины ωn >17.

Если рассмотреть расположения лёссовых грунтов в целом по Казахстану, то они с небольшими перерывами тянутся от северного конца хребта Каратау к Туркестану и к Шымкенту. Южнее он широко распространен в долине реки Келес и в районе г. Ташкента. Лёссовые грунты этих регионов различаются по условиям образования и литологическому составу. Встречаются места с лёссовыми грунтами однородного состава, в других местах лёссы содержат прослойки песка, гравия и подстилаются галечниковыми отложениями. В отдельных районах слои лёссовых грунтов чередуются с толстыми слоями глин. В Заилийском Алатау лёссовые грунты залегают сплошным покровом на склонах горных хребтов и в предгорной равнине на высоте от 200–500 до 2000 м. Толщина слоя изменится от долей метров до нескольких десятков метров. В районе Текели, по некоторым данным, толщина слоя лёссового грунта достигает 10 м, а в районе Алма-Аты толщина слоя лёссового грунта составляет 6–7 м, местами достигая 10 м и более. В пределах Чуйской долины над слоем галечников залегают лёссовые грунты различного геологического происхождения. Толщина слоя лёссов местами достигает десятков метров. В то же время в некоторых районах Шымкентской области толщина слоя лессовых грунтов колеблется от 6 до 20 м и более.

В глинистых грунтах деформирование под действием статической нагрузки обусловлено, главным образом, взаимным перемещением твердых частиц грунта. При этом различают объемные деформации и деформации формоизменения грунтов. Объемная сжимаемость глинистых водонасыщенных грунтов возможна лишь при отжатии воды из пор грунта. Поскольку поры грунта малы и, кроме того, часть их объема, как сказано выше, занята связной водой, то отжатие свободной воды происходит медленно и состояние деформирования грунта, растягивается часто на длительный промежуток времени. При этом для получения связи между напряжением и деформацией (типа 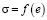) могут быть использованы приборы, называемые стабилометрами трехосного сжатия, в которых известны все компоненты тензора напряжений и тензор деформации, т.е. в которых можно исследовать свойства грунтов в условиях сложного напряженного состояния. Процесс одномерной деформации моделирует прибор, так называемый одометр. Он дает возможность установить компрессионную зависимость между напряжением и деформацией, т.е. 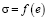. При этом характеристики грунтов, которые определяют их напряженно-деформированные состояния, являются переменными величинами и зависят от многих факторов.

Далее будем пользоваться уравнением механики уплотняемых трёхфазных грунтов, полученным в [7], которое в общем виде запишется так:

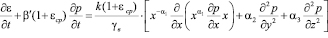. (1)

Причём здесь, когда

, , ,

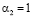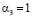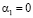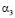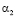задача соответствует трёхмерной; когда =0, =1, 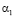=0, задача соответствует двумерной; когда

, , ,

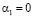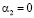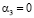задача соответствует одномерной; когда

, , ,

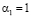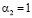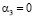задача соответствует осесимметричной; 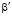– коэффициент объёмного сжатия; k – коэффициент фильтрации; εср – средний коэффициент пористости; γ – объёмный вес воды; р – давление в поровой жидкости. Здесь выражение 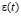для трехосного напряженно-деформированного состояния запишется так:

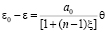, (2)

где θ – сумма главных напряжений; n – размерность задач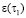и; и 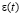соответственно коэффициенты пористости для начального и конечного моментов времени; ξ – коэффициент бокового давления грунта; а0 – коэффициент мгновенного уплотнения. Причем а0 называется коэффициентом мгновенного уплотнения, и чем больше величина а0, тем сильнее уплотняется грунт, поэтому этот параметр называется коэффициентом уплотнения. Однако коэффициент уплотнения или уплотняемость грунта по мере увеличения напряжений постепенно уменьшается. Причем коэффициенты уплотнения для слабоуплотняемых глин достигают значений а0 = 0,10–0,01 МПа, а для уплотненных глин уменьшаются до значений а0 = 0,05–0,01 МПа.

Уравнение (1) при (2) для трёхфазной грунтовой среды, обладающей только упругим свойством, имеет вид:

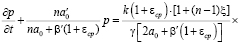
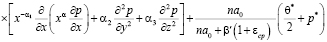. (3)

Выражение (3) для двухфазной грунтовой среды представляется так:

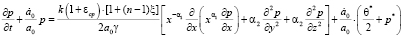.(4)

При этом начальное условие имеет вид:

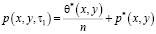, (5)

где τ – время приложения нагрузки; t – время, для которого определяется деформация.

Явления уплотнения водонасыщенных глинистых грунтов связаны с уменьшением объема пор. Следовательно, это явление сопровождается с удалением из пор грунта некоторого количества жидкости, находившейся в нем. В тех случаях, когда скорость процесса уплотнения глинистого грунта определяется только скоростью удаления жидкости из пор грунта, то процесс уплотнения сопровождается значительным повышением давления в воде, заполняющей поры грунта, и возникновением напряженного состояния в скелете грунта. Эти случаи оказывают существенное неблагоприятное влияние на устойчивость оснований сооружений и земляных откосов. По окончании процесса уплотнения давление в воде падает и устойчивость таких сооружений улучшается. Причем время процесса уплотнения изменяется от малых промежутков до больших, даже до десятков лет. Ее длительность, в основном, зависит от вида и свойств грунта, а также от размеров уплотняемой области. При этом состояние, возникающее в скелете грунта и в жидкости, называется нестабилизированным напряженным состоянием, а после окончания явления уплотнения его называют стабилизированным. Если же скорость процесса уплотнения определяется скоростью вязко-пластических деформаций грунта, а не скоростью удаления воды, то процесс уплотнения обычно не сопровождается повышением давлений в жидкости.

Таким образом, процессы сжатия грунта, связанные со временем, могут существенно повлиять на характер работы основания и сооружения. Следовательно, они должны быть учтены при проектировании. Чтобы судить о размерах будущей осадки грунта под фундаментом, надо знать зависимость изменения пористости от изменения давления.

Ниже рассмотрим процесс уплотнения двухфазной грунтовой массы, когда коэффициент уплотнения считается переменным только во времени, т.е. 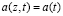. Причем величина а аналогична обратной величине модуля деформации грунта Е.

Уравнение одномерного уплотнения такой среды имеет вид:

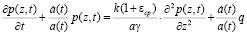, (6)

где р – давление в поровой жидкости; t – время; z – координата; q – распределенная нагрузка, зависящая от времени; 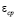– средний коэффициент пористости; 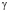– объемный вес воды; а – коэффициент уплотнения. Здесь при выводе уравнения (6) использовано уравнение равновесия

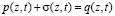(7)

и обозначения

;

.

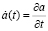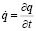Полученное уравнение (6) решим применительно к расчетной схеме, когда грунтовая масса мощности h подвергается уплотнению под действием внешней равномерно распределенной нагрузки с интенсивностью q. Причем верхняя поверхность уплотняемого слоя водопроницаема, а нижняя – нет.

Краевыми условиями этой задачи будут

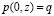, (8)

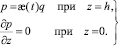(9)

Действительно, давление в поровой жидкости в начальный момент времени 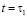принимает значение p = q, а далее с увеличением t падает до нуля. Поэтому, если введем некоторую убывающую функцию æ(t), значение которой меняется в пределах [1,0), то граничные условия на поверхности слоя грунта будут неоднородными. При этом, когда æ(t) = 0, то по всем поверхностям слоя грунта получим однородные граничные условия. Таким образом, математическая постановка данной задачи сводится к следующему: требуется определить непрерывную функцию 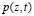, отражающую закон распределения давлений в поровой жидкости из дифференциального уравнения (6) при начальном (8) и граничных (9) условиях.

Уравнение (6) решается при неоднородных граничных условиях. Для решения его при краевых условиях (8) и (9) введем новую непрерывную функцию

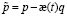. (10)

Тогда уравнение (6) приводится к следующему неоднородному дифференциальному уравнению

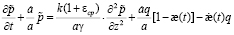, (11)

Оно при 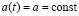и æ(t) = 0 приводится к уравнению, исследованному К. Терцаги [6], Н.А. Цытовичем [7], В.А. Флориным [8].

При этом краевыми условиями для функции 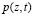будут:

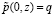, (12)

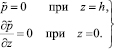(13)

Общее решение уравнения (11) при (12) и (13) после некоторых математических операций можно представить в виде:

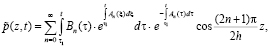(14)

где

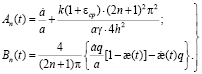(15)

Выражение (14) при (15), подставив в (10) для определения давлений в поровой жидкости, находим следующую расчетную формулу:

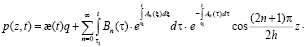(16)

Тогда напряжение в скелете грунта находится из условия равновесия

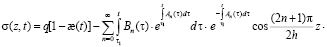(17)

Вертикальные же перемещения верхней поверхности уплотняемого грунтового массива мощностью h находятся из известной зависимости [6]. Она для грунтов с переменным во времени коэффициентом уплотнения имеет вид:

,

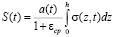Откуда находим

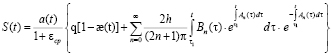. (18)

Выражения (16)–(18) можно принять за расчетные формулы нахождения давления в поровой жидкости, напряжения в скелете грунта и величину осадка уплотняемого грунтового массива соответственно, когда модуль деформации изменяется в зависимости от времени.

Пусть 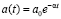и функция æ(t) имеет вид

æ(t) = æ0 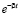, (19)

где æ0 = 1 при t = 0 и æ(t) при t>æ равна 0.

Тогда выражение (15) имеет вид

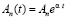, (20)

где

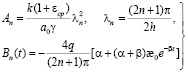. (21)

В то же время .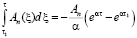

Так как в данной задаче нас интересует значение порового давления 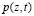в течение длительного промежутка времени после начала процесса фильтрационного уплотнения, кроме того, экспоненциальная функция быстро убывает при больших значениях показателя, то в соответствующих рядах достаточно ограничиваться только несколькими членами. Причем значение интеграла

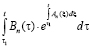
вычислим пользуясь формулой трапеции, взяв шаг h/10.

Подставив полученное значение интеграла в соответствующие формулы (16)–(21), находим значение порового давления, напряжения в скелете грунта и осадок уплотняемого массива во времени и координат.

Следует заметить, что полученное решение задачи является более общим, чем соответствующие решения К. Терцаги [6], Н.А. Цытовича [7], В.А. Флорина [ 8].

Анализ теоретических кривых «поровое давление – время» и «осадка – время» дает, что эти величины во многом зависят от того, в какой степени учтены деформационные и фильтрационные свойства грунта при решении задачи уплотнения. Учет переменности во времени коэффициента сжимаемости дает возможность точнее понять процесс консолидации земляных масс. При переменном во времени коэффициенте сжимаемости распределение внешней нагрузки между давлением в поровой жидкости и напряжением в скелете грунта происходит быстрее, чем при постоянной величине этого параметра, а осадок слоя грунта не меняет своего стабилизированного состояния.

Однако результаты исследований Н.Н. Маслова [5], М.Н. Гольдштейна [1], В.А. Флорина [8], Н.А. Цытовича [7] показали, что скорость уплотнения глинистого грунта существенно зависит не только от условия оттока отжимаемой воды, но и от условий проявления ползучести скелета грунта. Ползучесть является одним из частых проявлений реологических свойств физических тел. Характерным признаком ползучести служит длительная слабо затухающая во времени деформация тела под воздействием неизменной по величине нагрузки, приложенной к телу.

По своей природе глинистые грунты также относятся к реологическим телам и деформации, связанные с явлением ползучести, находят обычно свое отражение в уплотнении земляных масс со скоростями, не превышающими нескольких сантиметров в год. Вместе с тем процесс уплотнения основания сооружения может находиться в медленном непрекращающемся движении без всяких признаков окончательной его стабилизации. Несмотря на такую незначительную интенсивность деформации, они в ряде случаев могут оказаться недопустимыми для сооружений, расположенных на деформируемом основании. Особенно в подобных условиях разрушаются сами здания и сооружения, на построение которых уходят большие средства. Примером и подтверждением этого утверждения могут служить многочисленные здания города Шымкента, расположенные в пределах медленно уплотняющихся грунтовых оснований. В результате их неравномерной осадки, связанных с ползучестью грунтов, они становятся уже непригодными еще до эксплуатации.

Для описания вязких свойств грунтов пользовались различными их механическими моделями, состоящими из пружин, цилиндров с поршнями, наполненных жидкостью и из жестко-пластических тел. При этом пружина и вязкие элементы дают достаточное представление соответственно об упругих, подчиняющихся закону Гука, и вязких свойствах грунта, подчиняющихся закону движения ньютоновской жидкости. Механическое поведение таких моделей под нагрузкой и во времени описывалось реологическими уравнениями состояния грунтов, которые связывают между собой его деформацию, напряжение и их производные по времени и имели они вид линейного дифференциального уравнения. Позднее для решения задач уплотнения грунтовых сред были применены интегральные соотношения. Одним из первых, кто применил их для описания состояния скелета грунта, был В.А. Флорин [8]. При этом связь между коэффициентом пористости грунта ε и суммой главных напряжений в скелете им принята в виде линейной зависимости. Следует заметить, что некоторые вопросы этих задач исследованы в [2–4, 9].

Библиографическая ссылка