Известно [1], что антенна эффективно излучает энергию, если ее характерный размер сравним с длиной волны излучения. Если размеры антенны заметно меньше длинны волны, то сопротивление излучению существенно падает, и для восстановления эффективности излучения необходимо дополнительно ее модифицировать. Существует достаточно много различных способов, как, например, покрытие антенны керамикой или использование у-колена [2]. Однако, на данный момент все существующие способы решения достигли предела своей эффективности. Поэтому необходим новый способ, который с одной стороны поможет существенно улучшить излучательно-приемные характеристики антенны, размеры которой много меньше длины, а с другой стороны, не приведет как к существенному удорожанию, так и к увеличению массогабаритных характеристик.
Одним из наиболее перспективных направлений в технологии электрически малых антенн последних десятилетий считается использование метаматериалов с отрицательными значениями диэлектрической и/или магнитной проницаемостями. Обзорные статьи [3–6] посвящены использованию метаматериалов в технике антенн в диапазоне частот от 0,1 до 100 ГГц. Основные направления связаны с достижением широкополосности и уменьшением размеров антенных элементов, компенсацией реактивности электрически малых антенн в широкой полосе частот, достижением узкой пространственной направленности элементарных излучателей. Однако, анализ опубликованных статей показал, что расчеты и изготовление антенн в метаматериале ведутся на частотах, превышающих радиочастотный диапазон – порядка нескольких ГГц и более. В связи с этим актуальным видится направление применения метаматериалов в антенной технике в радиочастотном диапазоне. Данная статья посвящена разработке и апробации полосковой антенны, покрытой метаматериалом.
Экспериментальная часть
Метаматериалы обычно представляют собой периодичные структуры, поэтому достаточно произвести моделирование одной элементарной ячейки с установкой периодических граничных условий. Вычисление характеристик структур в таких расчётах производится при фиксированных геометрических параметрах резонаторов и их ориентации в самом метаматериале, количество и время вычислений возрастают пропорционально их числу, что не всегда удобно. В этом случае можно воспользоваться периодичностью метаматериалов и проводить вычисление их характеристик в два этапа. На первом этапе проводится расчет отдельного резонатора, а на втором, по определённым свойствам, вычислять отклик всей структуры.
Рассмотрим соответствующий подход более подробно. Наиболее эффективным резонатором, входящим в состав метаматериала, для нашей задачи является П-образный резонатор. Остановимся на простой модели, позволяющей оценить его свойства, и рассчитать эффективные параметры объёмной структуры, состоящей из таких резонаторов.
Простейшей моделью, позволяющей оценить характеристики П-образного резонатора, является модель сосредоточенного колебательного контура. Можно представить, что частица состоит из емкости C и индуктивности L (рис. 1). Такой подход широко используется в литературе [4].
Проводя прямую аналогию между геометрическими параметрами резонатора и колебательного контура, емкость определяется сечением резонатора и шириной ёмкостного зазора:
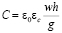 ,
,
где eо – диэлектрическая постоянная, eС – относительная диэлектрическая проницаемость в ёмкостном зазоре, w и h – поперечные размеры зазора, g – величина зазора. Тогда индуктивность, пропорциональная отношению площади соленоида, образованного резонатором, к его высоте:
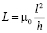 ,
,
где µo – магнитная постоянная.
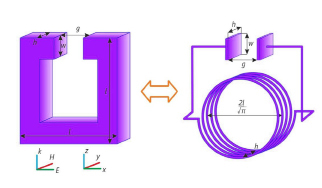
Рис. 1. П-образный резонатор и колебательный контур. Показана ориентация резонатора относительно координатных осей и падающего поля
Резонансная частота колебаний контура следующая:
 ,
,
где с0 – скорость распространения электромагнитных излучений в вакууме. Таким образом, если пропорции резонатора зафиксированы и окружающая резонатор среда не имеет дисперсии, то изменение его длины стороны приводит к пропорциональному линейному сдвигу резонансной длины волны. Кинетическую энергию движения электронов можно определить с помощью постоянной кинетической индуктивности в колебательном контуре:
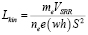 ,
,
где е – заряд электрона, mе – масса электрона в металле, nе – концентрация электронов, VSRR – объём резонатора.
Пусть резонатор ориентирован по отношению к падающему полю так, как показано на рис. 1, и период расположения резонаторов рху и pz поперёк волнового вектора и вдоль, соответственно. Тогда фактор заполнения метаматериала определяется следующим соотношением:
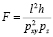 .
.
По известным поляризациям выводятся соотношения для характеристик метаматериала:
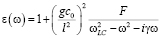 ;
;
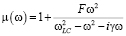 ;
;
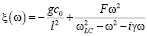 ;
;
где g = R/L – коэффициент поглощения эквивалентного контура, R – сопротивление x – параметр бианизотропии.
Математическая модель полосковой антенны, излучающей в безграничном однородном пространстве, в настоящее время хорошо представлена в литературе [7]. Теория антенн, покрытых оболочкой, в частности из метаматериала, довольно сложна. Поэтому было принято решение отказаться от аналитического подхода для описания работы антенн, покрытых метаматериалом, а проводить численный анализ работы антенн путем прямого решения уравнений Максвелла, дополненных материальными уравнениями для среды из метаматериала, которые могут быть записаны в следующем виде:
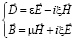 .
.
Численное решение системы уравнений проводилось в двумерной, так и в трехмерной геометрии. Использование двухмерной модели позволяло экономить машинное время и, соответственно, перебрать большое количество входных параметров задачи.
Расчёт производился на специальной пространственной сетке, изображенной на рис. 2. Шаг сетки определяется из минимального характерного размера системы (длина ЭМ-волны, минимальный геометрический размер излучающей антенны, толщина слоя из метаматериала).
а) б)
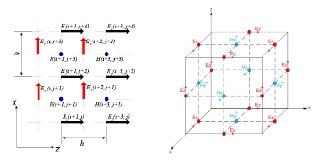
Рис. 2. Пространственная сетка для решения системы уравнений Максвелла методом FDTD: а – в двухмерной геометрии; б – в трехмерной геометрии
На рис.3 представлено электрической поле полосковой антенны, с размерами намного меньше длины волны излучения, покрытой метаматериалом с П-образными резонаторами, рассчитанное методом FDTD в двухмерной геометрии.
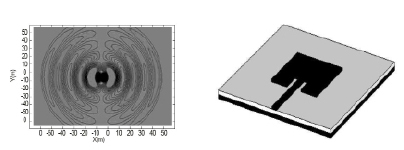
Рис. 3. Распределение электрического поля симметричной антенны, с размерами намного меньше длины волны излучения, покрытого метаматериалом с П-образными резонаторами, рассчитанное методом FDTD в двухмерной геометрии. Справа представлена схема полосковой антенны с размерами подложки 7x7 см, полоска 3x3 см; диэлектрик – фторопласт толщиной 4 мм
В численном моделировании в работе задавались следующие параметры: электрофизические свойства метаматериала – e=–1,1; m=1,01; x=0,0025; частота излучения – f=300 МГц, размеры антенны – 3x3 см.
Основным результатом численных расчетов является нахождение оптимальной толщины покрытия из метаматериала с П-образными резонаторами для полосковой антенны, обеспечивающего максимальную эффективность работы антенны. На рис. 4 представлена зависимость отношения квадрата электрического поля антенны в дальней зоне при наличии оболочки из метаматериала с П-образными резонаторами к квадрату электрического поля антенны без оболочки в зависимости от толщины b покрытия из метаматериала. В численном моделировании задавались те же параметры. Максимальная эффективность антенны наблюдается при толщине покрытия из метаматериала b=2,8 мм. Электрофизические параметры покрытия рассчитывались на основе приведенных выше формул математической модели, описывающей метаматериал с П-образными резонаторами. Размеры и параметры резонаторов подбирались для частотного диапазона 260–340 МГц.
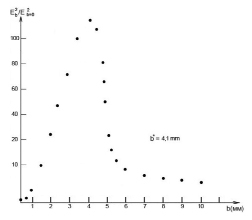
Рис. 4. Зависимость отношения квадрата электрического поля антенны в дальней зоне при наличии оболочки из метаматериала к квадрату электрического поля антенны без оболочки в зависимости от толщины b покрытия из метаматериала
Для экспериментальной проверки результатов была создана электрически малая полосковая антенна. Для изготовления метаматериала для частоты 300 МГц с целью удержания П-образных резонаторов был залит тонкий слой синего силикона, в который после частичного затвердевания были помещены П-образные резонаторы. При этом силикон доступен по цене и поглощение электромагнитной волны на частоте 300 МГц достаточно мало, тангенс угла диэлектрических потерь порядка 10–4. Далее полученный образец метаматериала наносился на антенну. В связи с тем, что исследование излучательно-приемных характеристик антенны необходимо проводить в дальней зоне, где расстояние между антеннами в несколько раз превышает длину волны, расстояние между антеннами было выбрано порядка 6 метров, что в несколько раз превышает длину волны излучения на частоте 300 МГц. На рис. 5 представлена частотная зависимость коэффициента отражения для антенны с покрытием метаматериала (а) и без (б).
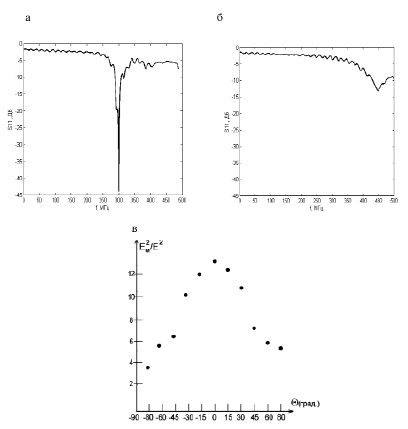
Рис. 5. Экспериментальное исследование характеристик изготовленной антенны. Частотная зависимость коэффициента отражения антенн: а – с применением метаматериала; б – без него; в – диаграмма направленности антенны, покрытой слоем метаматериала
В ходе эксперимента было установлено (рис. 5 в), что мощность излучения антенны, покрытой слоем метаматериала, возрастает до 10 раз по сравнению с антенной, не покрытой метаматериалом. Так как это был первый пробный эксперимент с созданным вручную метаматериалом, из-за ряда потерь и неидеальности выполнения покрытия метаматериалом результаты эксперимента оказались несколько ниже теоретически ожидаемых.
Выводы
По результатам численного расчета был изготовлен и нанесен на антенну слой метаматериала, состоящего из П-образных резонаторов, и проведено экспериментальное исследование. В ходе эксперимента было установлено, что покрытие антенны метаматериалом приводит к обужению диаграммы направленности, что также предсказывается теоретически, но важно отметить, что, тем не менее, в любом направлении наблюдается заметное увеличение амплитуды сигнала. Что свидетельствует о том, что покрытие антенны метаматериалом заметно повышает эффективность излучения, до 10 раз, а также подтверждает правильность работы рассчитанного нами алгоритма.
Данная работа выполнена при поддержке гранта ФСРМФПНТС, госконтракт 10234ГУ2/2015 от14.06.2016.
Библиографическая ссылка
Селезнев А.Д., Пачурин Г.В., Галка А.Г. РАЗРАБОТКА ЭЛЕКТРИЧЕСКИ МАЛЫХ АНТЕНН С ПРИМЕНЕНИЕМ МЕТАМАТЕРИАЛА // Международный журнал прикладных и фундаментальных исследований. 2017. № 9. С. 39-44;URL: https://applied-research.ru/ru/article/view?id=11822 (дата обращения: 15.01.2026).

