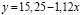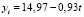Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Омарова М.Т. 1

---

1 Карагандинский экономический университет Казпотребсоюза

Согласно данным Комитета по статистике МНЭ РК, уровень бедности в Казахстане снижается значительными темпами. Рассматривая же уровень бедности в разрезе регионов по Казахстану, следует отметить, что наиболее высокие значения в 2015 году зарегистрированы в Южно-Казахстанской (5,3 %), Северо-Казахстанской (3,7 %) областях, наименьшие отмечаются в городах Астана (0,6 %) и Алматы (0,6 %). Поскольку самый высокий показатель уровня бедности приходится на Южно-Казахстанскую область, был проведен анализ и прогнозирование временного ряда уровня бедности населения Южно-Казахстанской области за 2001–2016 гг. Таким образом, можно сделать вывод: трендовая модель и модель Р. Брауна адекватны имеющемуся динамическому ряду уровня бедности населения в Южно-Казахстанской области РК, и полученные прогнозы отличаются между собой незначительно.

Статья в формате PDF

1529 KB

уровень бедности населения Южно-Казахстанской области

анализ

прогнозирование

трендовая модель

модель экспоненциального сглаживания

1. Прогнозирование мировой экономики и мировых товарных рынков: Учебное пособие / Н.К. Емелина. – Караганда, Карагандинский экономический университет Казпотребсоюза, 2015. – 130 с.

2. Коломейко М.В. Анализ основной тенденции и прогнозирование уровня бедности населения Астраханской области на основе методов временных рядов // Экономика, статистика и информатика. – № 4. – 2014. – C. 154–157.

3. Комитет по статистике Министерства Национальной Экономики Республики Казахстан [Электронный ресурс]. – URL: http://www.stat.gov.kz/ (дата обращения 15.03.2017).

Официальная статистика при определении численности бедного населения в Казахстане ориентируется на абсолютную концепцию бедности. Согласно данному подходу, живущими за чертой бедности считаются граждане, которые имеют доходы ниже официально установленного прожиточного минимума в данном регионе. Согласно Закону Республики Казахстан «О прожиточном минимуме» от 16 ноября 1999 года №474 «черта бедности – это граница дохода, необходимого для удовлетворения минимальных потребностей человека, устанавливаемая в республике в зависимости от экономических возможностей».

Доля населения, которые имеют доходы ниже величины прожиточного минимума, в 2015 году составила 2,7 %, т.е. мы видим уменьшение в 2,04 раза по сравнению с 2011 годом. Вместе с тем, сохраняется значительная дифференциация доходов в городской и сельской местности.

Согласно данным Комитета по статистике МНЭ РК, уровень бедности в Казахстане снижается значительно. Так, с 2011 года уровень бедности страны снизился с 5,5 % до 2,7 % в 2015 году [3], при этом, учитывая, что в 2015 году произошло значительное снижение доходов населения, и, в принципе, общая экономическая ситуация страны оставляла желать лучшего. Девальвация 2015 года привела к тому, что показатель бедности снизился незначительно, всего на 1 %. Как мы знаем, цены потребительских товаров и услуг в Республике Казахстан в значительной мере зависят от курса тенге к доллару, это ежемесячно подтверждается уровнем инфляции, таким образом, влияние курса валюты на уровень бедности в стране можно отнести к прямому фактору. Так, в городской местности доля населения с доходами ниже величины прожиточного минимума составила 1,3 %, а в сельской местности 4,4 %, т.е. уровень бедности в сельской местности превысил городской уровень в 3,4 раза. Рассмотрим уровень бедности в разрезе регионов на рис. 2.

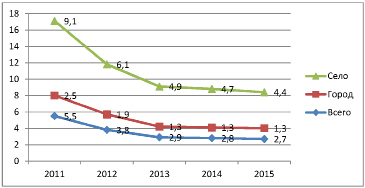
Рис. 1. Динамика уровня бедности в Республике Казахстан за 5 лет (в %)

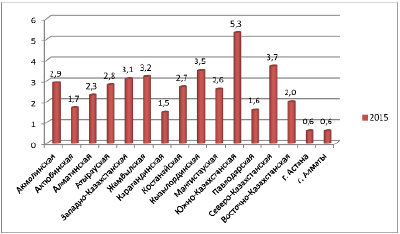
Рис. 2. Доля населения, имеющего доходы ниже величины прожиточного минимума по регионам в 2015 году (в %)

Как мы видим на рисунке 2, наиболее высокие значения в 2015 году зарегистрированы в Южно-Казахстанской (5,3 %), Северо-Казахстанской (3,7 %) областях, наименьшие же отмечаются в городах Астана (0,6 %) и Алматы (0,6 %). Поскольку самый высокий показатель уровня бедности по РК приходится на Южно-Казахстанскую область, проведем трендовый анализ временного ряда уровня бедности населения Южно-Казахстанской области за 2001–2016 гг. на основе данных табл. 1. Выясним, существует ли тенденция в динамическом ряду показателя бедности населения Южно-Казахстанской области, и только после этого будем переходить к определению тенденции и выделять тренд.

Таблица 1

Динамика показателя бедности населения Южно-Казахстанской области, %

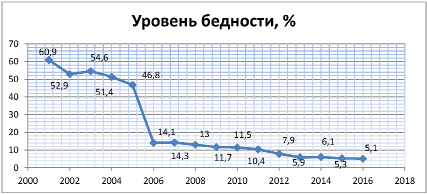
Рис. 3. Динамика уровня бедности населения Южно-Казахстанской области за 2001–2016 гг. Разработано автором на основе источника: статистические данные Комитета по статистике МЭН РК

Покажем график уровня бедности в Южно-Казахстанской области РК с 2001 по 2015 годы (рис. 3).

Исходя из данных рис. 3, в целом наблюдается положительная динамика снижения уровня бедности в Южно-Казахстанской области, но в 2003 году показатель повысился на 1,7 % по сравнению с 2002 годом, а в 2007 году повышение показателя уже на 0,2 % по сравнению с 2006 годом; повышение уровня бедности связано с нестабильностью финансовой системы Казахстана, а именно влиянием мирового финансового кризиса. С 2008 года наблюдается снижение показателя, что связано с принятием социально значимых программ.

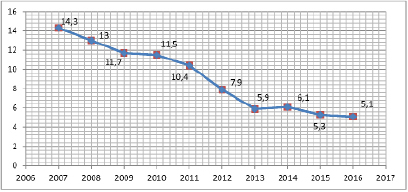
Рис. 4. Динамика показателя бедности населения Южно-Казахстанской области за 2007–2016 гг. Разработано автором на основе источника: статистические данные Комитета по статистике МЭН РК

На рис. 4 видим, что с 2007 года наблюдается тенденция к сокращению уровня бедности населения, поэтому для анализа изучаемого процесса с помощью метода временных рядов будем использовать новый ряд динамики уровня бедности населения Южно-Казахстанской области с 2007 по 2016 годы [2, стр. 154–156].

Используя инструмент анализа «Регрессия» (Анализ данных в Excel), получаем уравнение тренда

y=15,25–1,12x. (1)

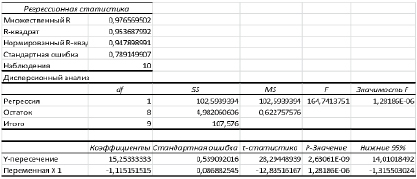
Рис. 5. Протокол регрессионного анализа. Разработано автором на основе статистических данных с помощью инструмента анализа «Регрессия»

Необходимо проверить статистическую значимость уравнения регрессии в целом и статистическую значимость коэффициентов уравнения. Из рис. 5 видно следующее:

– коэффициент детерминации достаточно близок к 1, что говорит о тесной связи между показателями;

– уровень значимости возьмем равный 5 %;

– при данном уровне значимости наблюдаемые значения F-критерия Fнабл=164,74 и t-статистик ta = 28,3, tb = – 12,8.

Критическое значение F-критерия при этом уровне значимости, числе степеней свободы 1 и (n–2) можно определить либо по таблице F-критерия Фишера либо с помощью Статистической функции F.ОБР.ПХ(0,05; 1; 8). Определим вторым способом: Fкрит = 5,32. Сравним наблюдаемое значение критерия с критическим значением: уравнение регрессии статистически значимо и надежно.

Оценку же статистической значимости параметров регрессии проведем с помощью t-статистики Стьюдента. Критическое значение t-статистики при данном уровне значимости и числе степеней свободы (n–2) можно определить либо по таблице t-статистики Стьюдента либо с помощью Статистической функции СТЬЮДЕНТ.ОБР.2Х(0,05; 8). Определим с помощью функции: tкрит = 2,31. Также надо сравнить наблюдаемое значение критерия с критическим значением: так как наблюдаемые значения t-статистики параметров уравнения регрессии ta и |tb| превосходят критическое значение, то нулевая гипотеза о равенстве нулю а и b отклоняется в пользу альтернативной, то есть параметры регрессии не случайно отличаются от нуля и являются статистически значимыми.

Из уравнения (1) имеем:

– коэффициент при переменной х в этой регрессии показывает, что уровень бедности населения Южно-Казахстанской области в рассматриваемый период ежегодно уменьшался на 1,12 %;

– константа в этой регрессии также имеет экономический смысл, т.е. она показывает, что уровень бедности населения в РК в 2007 году составлял примерно 15,3 %;

– прогнозы на 2017 и 2018 годы получим следующие:

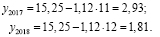
Учитывая уравнение (1), прогноз уровня бедности населения Южно-Казахстанской области в 2017 году будет равен 2,93 %, а в 2018 году является равным 1,81 %.

Одними из наиболее перспективных в исследовании и прогнозировании одномерных временных рядов считаются адаптивные методы. Адаптивными называются методы прогнозирования, которые позволяют строить самокорректирующиеся (самонастраивающиеся) экономико-математические модели, способные оперативно реагировать на изменение условий путем учета результатов прогноза, сделанного на предыдущем шаге, и учета различной информационной ценности уровней ряда.

Модель экспоненциального сглаживания является основой для построения адаптивных методов прогнозирования. Один из первых методов прогнозирования, основанный на экспоненциальном сглаживании, предложил Р. Браун. Существует несколько модификаций и развитий метода Брауна: модель Ч. Хольта, модель Дж. Бокса и Г. Дженкинса и др. [1, стр. 88].

Рассмотрим линейную адаптивную модель Брауна для данных рис. 4. Решаем пошагово:

по первым пяти точкам временного ряда оцениваем значения а0 и а1 параметров модели с помощью МНК для линейной модели 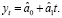Для этого используем статистическую функцию ЛИНЕЙН в Excel и получим следующее уравнение:

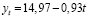. (2)

Затем выбираем параметр сглаживания α = 0,3, и тогда коэффициент дисконтирования β = 0,7.

Вычисляем начальные условия экспоненциальных средних:

Находим значения экспоненциальных средних для следующего периода:

Корректируем параметры модели 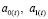, т.е. для периода t=1 получим:

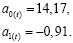
По модели с корректированными параметрам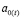и и 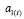находим прогноз на следующий период времени: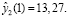

Возвращаемся к шагу 3, вычисления производим до конца наблюдений.

Все рассчитанные значения представлены на рис. 6.

Из рис. 6 мы видим прогнозные значения на 2017 и 2018 годы, учитывая формулу

,

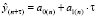равные следующим значениям:

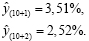
Результаты прогнозных значений, которые получены по уравнениям линейного тренда и линейной адаптивной модели Р. Брауна, представлены в табл. 2.

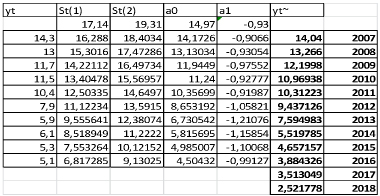
Рис. 6. Расчетная таблица для вычисления прогноза с помощью модели экспоненциального сглаживания. Составлено автором на основе данных рис. 4 в среде Excel

Таблица 2

Прогнозные модели и значения уровня бедности населения в Южно-Казахстанской области РК в 2017 и 2018 годах

Составлено автором на основе уравнений (1), (2) и рис. 6.

На основании табл. 2 можно сделать вывод, что трендовая модель и модель Р. Брауна показали примерно одинаковый результат прогноза (разница только в 0,6–0,7 %), что позволяет судить о точном прогнозе.

Таким образом, осуществив анализ и прогнозирование уровня бедности на основе динамического ряда 2001–2016 гг., можно сделать вывод, что во временном ряду присутствует тенденция, полученные модели адекватны имеющемуся динамическому ряду уровня бедности населения в Южно-Казахстанской области РК, полученные прогнозы отличаются между собой незначительно.

Библиографическая ссылка