Научный журнал

Международный журнал прикладных и фундаментальных исследований

ISSN 1996-3955

ИФ РИНЦ = 0,593

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Сембеков А.К. 1

---

1 Карагандинский экономический университет Казпотребсоюза

В настоящей статье рассматриваются основные показатели страховых рынков Евразийского Экономического Союза (ЕАЭС). В этом контексте проведен анализ страховых рынков ЕАЭС. По результатам анализа страховых рынков ЕАЭС осуществлен прогноз доли страховых премий к ВВП стран ЕАЭС до 2020 гг., рассчитываемый на базе авторегрессионных моделей. Результаты прогнозных расчетов показывают, что к 2020 году доли участия страховых компаний в ВВП в странах ЕАЭС будут иметь незначительные тенденции роста. С учетом полученных данных, авторами предложены основные рекомендации развития страховых рынков ЕАЭС. Проведенный прогноз сформирован на основе статистических данных за предшествующие периоды. Результаты прогнозных расчетов показывают, что к 2020 году доли участия страховых компаний в ВВП в странах ЕАЭС будут иметь незначительные тенденции роста: в Армении – 0,8, в Беларуси – 1,16, в Казахстане – 0,9, в Кыргызстане – 0,28, в России – 1,5. Полученные прогнозные показатели показывают, что в ближайшей перспективе в странах ЕАЭС не будет наблюдаться активное развитие страховых рынков. Это связано с низкими темпами развития страхования, низким потенциалом национальных страховых рынков стран ЕАЭС.

Статья в формате PDF

2276 KB

страхование

страховой рынок

конкурентоспособность

интеграция

страховая отрасль

страховой потенциал

методы прогнозирования

1. Методы прогнозирования в условиях рынка: Учебное пособие / Э.Е. Тихонов. – Невинномысск, 2006. – С. 13–15.

2. Финансовые организации в Евразийском экономическом союзе // Статистический сборник Евразийской экономической комиссии. – 2016. – С. 15–19.

3. Поспелова Е.С. Совершенствование регулирования экономики региона: На примере Самарской области: дис…. канд. эконом, наук. – Москва, 2006. – С. 117–118.

В современных условиях основной задачей интеграции является создание эффективного и конкурентоспособного единого страхового рынка ЕАЭС, способного реагировать на различные финансовые вызовы и угрозы. Конкурентоспособность страхового рынка обеспечивает его финансовый и инвестиционный потенциал. Потенциал для развития страховой отрасли, безусловно, определяется ее макроэкономическими условиями. В этой связи потенциал страховых рынков ЕАЭС можно оценить, обратившись к анализу динамики внутреннего валового продукта страны, поскольку утверждается, что при его росте, скорее всего, будет увеличиваться и доля страхования в ВВП.

Для определения конкурентных перспектив национальных страховых рынков стран ЕАЭС необходимо определить уровень их экономического развития по отобранным показателям и составить их прогноз. Попытаемся спрогнозировать развитие рынка на среднесрочный период. Прогноз будет основываться на зависимости между размерами рынка страхования и развитием национальной экономики – в частности ростом ВВП.

Для составления прогноза развития показателя доли страховых премий в ВВП нами использованы статистические данные, характеризующие уровень развития страховых рынков стран ЕАЭС за 2011–2015 годы (табл. 1).

По нашему мнению, из существующих методов среднесрочного прогнозирования наиболее приемлемым является метод трендовых прогнозных расчетов. При всех методах сглаживания временных рядов с целью выявления основной тенденции исходят, прежде всего, из фактического развития динамики в течение рассмотренного времени. Наиболее распространенным способом сглаживания временных рядов является метод наименьших квадратов. Математический аппарат метода наименьших квадратов подробно описан в научной литературе [2, с. 15–19].

Метод экстраполяции применяется при кратко- и среднесрочном прогнозировании. Его преимущества состоят в том, что он не требует обширной информационной базы и предполагает ее анализ с точки зрения информационной ценности различных членов временной последовательности.

Однако если временной ряд можно разложить на детерминированную составляющую и случайный компонент, то прогнозирование можно производить отдельно по обеим составляющим. Общий прогноз будет складываться из результатов этих двух прогнозов. В качестве модели прогноза случайного компонента мы выбрали авторегрессионную модель. При выборе вида тренда использовалась следующая методика. Критерием для выборки вида тренда служила величина среднеквадратической ошибки. В случае, когда среднеквадратические ошибки двух функций мало отличались друг от друга, предпочтение отдавалось функции более простого вида. При выборе аппроксимирующей функции также учитывалась информация о перспективах развития экономических субъектов в целом. [1, с. 13–15].

Нами предлагается механизм расчета прогноза показателей, доля страховых премий к ВВП стран ЕАЭС, на период 2016–2020 гг., рассчитываемый на базе авторегрессионных моделей.

Основывая свое решение на том, что если временной ряд можно разложить на детерминированную составляющую и случайный компонент, то прогнозирование можно производить отдельно по обеим составляющим. Общий прогноз будет складываться из результатов этих двух прогнозов. В качестве модели прогноза случайного компонента мы выбрали авторегрессионную модель [3, с. 117–118].

Для описания представленного временного ряда был выбран линейный тренд – показателей, доля страховых премий к ВВП стран ЕАЭС:

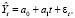(1)

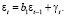(2)

Из (1) получаем

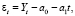
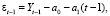
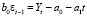
или

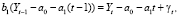
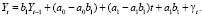
Тогда

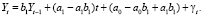
Из этого следует модель прогноза:

…

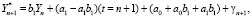
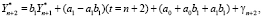
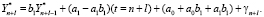
Вычисление доверительного интервала:

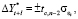(3)

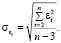(4)

Используя метод наименьших квадратов, были определены численные значения коэффициентов уравнения:

Y(t) = 0,464 + 0,027 t + Et.

Отклонения от тренда могут быть достаточно точно аппроксемированы авторегрессионной моделью:

et = 0,130et-1 + Ut.

В результате соответствующих преобразований получили следующую модель прогноза тренда показателей, доля страховых премий к ВВП стран ЕАЭС:

Yt* = 0,651Yt-1 + 0,024t + 0,407.

Таблица 3

Прогноз показателей, доля страховых премий к ВВП стран ЕАЭС, на период 2016–2020 гг.

Примечание. Таблица составлена на основе данных расчета.

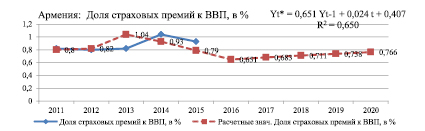
Рис. 1. Армения: Доля страховых премий к ВВП, в %

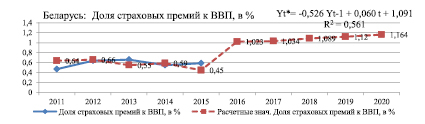
Рис. 2. Беларусь: Доля страховых премий к ВВП, в %

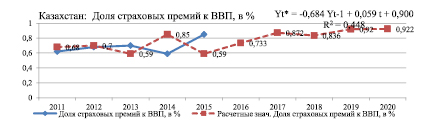
Рис. 3. Казахстан: Доля страховых премий к ВВП, в %

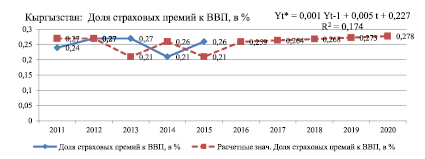
Рис. 4. Кыргызстан: Доля страховых премий к ВВП, в %

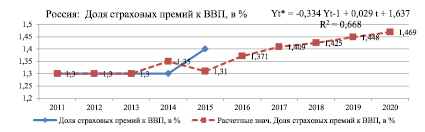
Рис. 5. Россия: Доля страховых премий к ВВП, в %

Проведенный нами расчет прогноза сформирован на основе статистических данных за предшествующие периоды. Результаты прогнозных расчетов показывают, что к 2020 году доли участия страховых компаний в ВВП в странах ЕАЭС будут иметь незначительные тенденции роста: в Армении – 0,8, в Беларуси – 1,16, в Казахстане – 0,9, в Кыргызстане – 0,28, в России – 1,5. Полученные нами прогнозные показатели показывают, что в ближайшей перспективе в странах ЕАЭС не будет наблюдаться активное развитие страховых рынков. Это связано с низкими темпами развития страхования, низким потенциалом национальных страховых рынков стран ЕАЭС. Активизация страхования возможна только вслед за общим оживлением экономической конъюнктуры. Дальнейшее развитие страхового рынка также во многом будет зависеть от прямой поддержки государства процессов интеграции отечественных страховщиков, предоставление особо благоприятного налогового режима, совершенствования бизнес-процессов страховых компаний, а именно использование современных форм страхового маркетинга, активного внедрения новых страховых услуг и продуктов.

Библиографическая ссылка