В настоящее время беспилотные летательные аппараты (БПЛА) способны решать практически любые задачи: предупреждение или управление чрезвычайными ситуациями, наблюдение и дистанционный сбор данных об объектах, сектор безопасности, включая патрулирование улиц городов, транспортных развязок или иных территорий. Также область применения БПЛА весьма обширна в таких областях как, пожарная безопасность, сельское хозяйство, рыболовство, лесничество, геодезия, картографирование местности, география, геология, строительство, средства массовой информации, кинематография, нефтегазовый сектор, энергетика. В БПЛА массой до 10 килограммов в качестве силовой установки наибольшее применение получили силовые установки, выполненные с использованием электрических двигателей [1, 2].
Таким образом, проведение исследований в области электродвигателей с возбуждением от постоянных магнитов является актуальным, несмотря на то, что содержит огромное количество сложных задач [3], решение которых создаст возможность для более широкого применения электродвигателей данного типа в различных отраслях науки и техники.
Постановка задачи
Реальная экспериментальная проверка и анализ режимов работы подобных сложных элементов, к которым относится электродвигатель с возбуждением от постоянных магнитов, представляет собой достаточно дорогостоящую и трудоёмкую задачу. Поэтому на одном из этапов разработки электродвигателя существенную помощь может оказать замена реального устройства виртуальной компьютерной моделью. При этом считается оправданным применение метода конечных элементов.
Широкое внедрение в инженерную практику различных методов автоматизации проектирования позволяет перейти от традиционного макетирования электродвигателя к построению его компьютерной модели с помощью специализированных программных комплексов. Это позволяет избежать больших материальных затрат, снизить вероятность ошибок при реализации новых решений, а также уменьшить время проектирования.
В настоящее время существует большое количество универсальных программ для моделирования электрических машин методом конечных элементов [4, 5]. В данном исследовании будет рассмотрен расчет двигателя с помощью пакета ELCUT.
Электродвигатель с постоянными магнитами для беспилотного летательного аппарата представляет собой электрическую машину, принцип действия которой основан на взаимодействии вращающегося магнитного поля статора и поля от постоянных магнитов ротора. В качестве постоянных магнитов используются материалы с высокой коэрцитивной силой, например сомарий-кобальт SmCo или неодим – железо – бор Nd-Fe-B.
Кроме того, в конкретном случае электродвигатель для БПЛА является электродвигателем обращенного типа – ротор располагается снаружи статора электродвигателя.
Алгоритм расчета электродвигателей подобной конструкции рассмотрен ранее [6–8].
Основные приемы работы в ELCUT
Первоначальный этап работы в программе ELCUT – при запуске создать новую задачу, задать имя файла и обозначить место сохранения документа (рис. 1).
Следующим этапом производится выбор типа и параметров новой задачи. Также программный комплекс позволяет изменить имя файла, в котором будут сохранены геометрическая модель и ее физические свойства. Далее в открывшемся диалоге из списка выбирается тип задачи (рис. 2). В данном случае в качестве типа задачи необходимо выбрать расчет магнитостатического поля. Выбранный модуль магнитостатики позволяет проводить расчет магнитного поля постоянных токов и/или постоянных магнитов, учитывая насыщение ферромагнитных материалов. Также модуль применим для таких расчетных примеров, как магнитные экраны исполнительные механизмы, электрические машины, приборы с постоянными магнитами. Кроме того, в данном диалоговом окне задаем единицы длины, координаты, метод расчета и класс модели. После осуществления выбора всех параметров задачи для дальнейшей работы необходимо нажать «Готово».
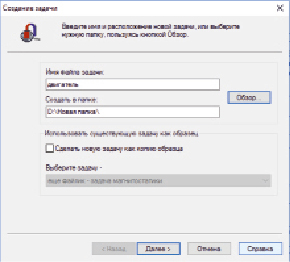
Рис. 1. Cоздание документа в ELCUT
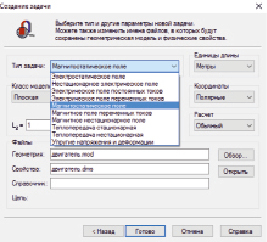
Рис. 2. Выбор типа задачи
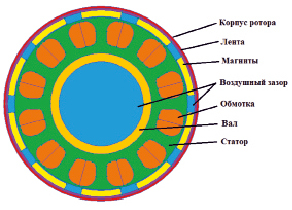
Рис. 3. Модель электродвигателя
Разработка модели
Разработку модели электродвигателя начнем с разбиения на составляющие (рис. 3).
Корпус ротора задаем свойствами метки блока, указываем относительную магнитную проницаемость и полярные координаты.
Также необходимо обозначить границу ротора, так как поле распространяется далеко за поверхность модели, для этого ограничиваем расчет поверхности только поверхностью машины. Другими словами, указываем метки ребер как границу ротора и далее задаем, что магнитный потенциал равен нулю, это в свою очередь означает, что поле не выходит за пределы наружной поверхности ротора (рис. 4).
Следующим этапом необходимо задать магнитную проницаемость постоянным магнитам, величину коэрцитивной силы каждого магнита и его направление, а также полярные координаты. При этом нужно учесть, что «направление» у каждого магнита будет свое.
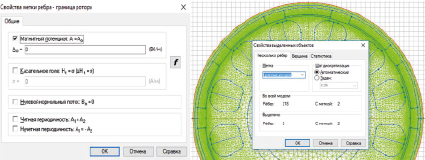
Рис. 4. Граничные условия и метки ребер границы ротора
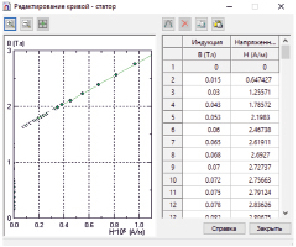
Рис. 5. Редактирование кривой статора
Далее аналогичным способом задаем воздушному зазору относительную магнитную проницаемость и полярные координаты.
Следующим этапом, на который необходимо обратить особое внимание, является задание свойств статора. В данном случае статору задаем тип магнитной проницаемости «нелинейный материал». При этом существует несколько способов описания свойств нелинейных магнитных материалов. В программном комплексе ELCUT описание магнитных материалов базируется на нормальной кривой намагничивания В(Н). Также можно указать коэрцитивную силу (намагниченность) для моделирования постоянных магнитов. В этом случае кривая сдвинется влево на величину коэрцитивной силы. Кроме того, указывается полярность координат. Задавая материал статора (рис. 5), можно воспользоваться библиотекой материалов пакета ELCUT [9].
Далее необходимо задать магнитную проницаемость вала, так как он не состоит из немагнитного материала (сплав алюминия), его магнитная проницаемость равна единице [10].
Также задаем обмотку статора, указывая магнитную проницаемость и полное число ампер-витков, соединенных последовательно, для каждой фазы.
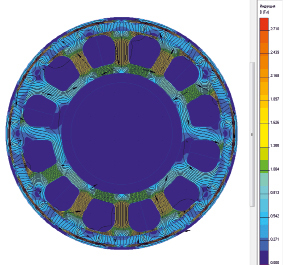
Рис. 6. Конечный результат модели с выполнением статора
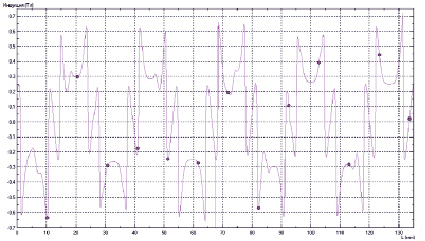
Рис. 7. График индукции в воздушном зазоре
И завершающим этапом решения задачи является построение сетки для модели. После чего необходимо модель с сеткой «решить» для получения конечного результата. При построении сетки конечных элементов есть возможность управлением ее густотой, в противном случае ELCUT построит сетку в автоматическом режиме. При этом применяется специальная технология, которая позволяет автоматически строить гладкую сетку, для того чтобы отказаться от выбора размера ячеек сетки.
Поставленная задача решается методом внешней итерации (метод Ньютона) и внутренней итерации (построение и факторизация матрицы).
Результаты моделирования
В результате расчетов получаем модель электродвигателя в программе ELCUT. Результаты моделирования представлены на рис. 6.
В рассчитанной модели особый интерес может возникнуть к распределению индукции в воздушном зазоре. Для того чтобы получить искомую характеристику, необходимо провести в воздушном зазоре произвольный контур и вывести график (рис. 7).
Заключение
В результате проведенного исследования определены основные сложности при моделировании электродвигателей, возникающие при способах задания магнитов на роторе и обмотки статора.
Освоены основные приемы работы с программой ELCUT и получена модель электродвигателя с постоянными магнитами.
Результаты исследования могут применяться при расчетах и моделировании электродвигателей с поверхностным распределением магнитов на роторе и распределенной обмоткой на статоре, а также когда существует равномерное распределение к полюсам разного количества магнитов по отношению к пазам. Учет указанных факторов позволит существенно ускорить этап проектирования электродвигателей подобной конструкции.
Данные исследования проведены при финансовой поддержке государства в лице Минобрнауки России (договор № 14.Z56.16.5570-МК).
Библиографическая ссылка
Лютаревич А.Г., Вяткина Е.А., Пугачева Е.А., Тевс В.В. МОДЕЛИРОВАНИЕ ЭЛЕКТРОДВИГАТЕЛЯ С ПОСТОЯННЫМИ МАГНИТАМИ // Международный журнал прикладных и фундаментальных исследований. 2017. № 12-1. С. 33-38;URL: https://applied-research.ru/ru/article/view?id=11958 (дата обращения: 11.02.2026).

