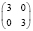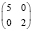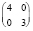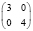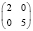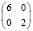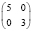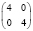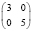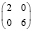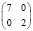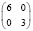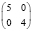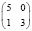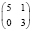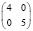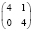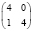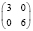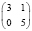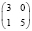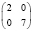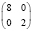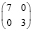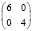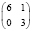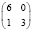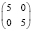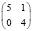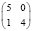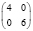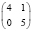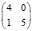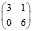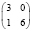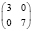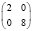В клинической практике достаточно частыми задачами, решаемыми статистическим исследованием, являются: установление идентичности сравниваемых групп больных по показателям, которые могут оказать влияние на результат лечения (к примеру, возраст, пол, тяжесть травмы или стадия заболевания и т.д.), диагностики или профилактики заболеваний; выявление различий в результатах лечения (к примеру, летальность, процент выхода на инвалидность, длительность койко-дня и т.п.); анализ статистической достоверности различий. Приведем такие примеры.
При оценке эффективности цитопротекторной терапии (двух-трех препаратов этой группы) при ишемическом инсульте необходимо определить, сопоставимы ли больные в этих группах по полу, возрасту, срокам развития ишемического процесса в мозге, по месту проживания. Вторым этапом анализа будет решение вопроса об эффективности препаратов, используемых для защиты клеток от ишемии. Такими показателями могут являться длительность утраты сознания, длительность периода нестабильности витальных функций, сроки регресса неврологической симптоматики и т.д. Помимо этого врачу-исследователю крайне важно оценить статистическую значимость установленных различий в исходах лечения в группах. Не являются ли они случайными? Необходимо выяснить – являются ли различия в группах следствием естественных различий, существующих в выборках, или разница возникла из-за того, что один из методов лечения или лекарственных препаратов оказался значимо эффективнее другого.
При изучении эффективности нового препарата (скажем, противовирусных препаратов – «старого» ацикловира и «нового» рибавирина) показателями эффективности лечения могут быть сроки купирования катаральных явлений, длительность температурного периода, выраженность и длительность интоксикационного периода, процент госпитализаций, наличие осложнений противовирусной терапии (диспепсия, нейротоксичность). В экспериментальных медицинских исследованиях статистически могут анализироваться частота появления обычных реакций организма экспериментального животного при каком-либо воздействии (скажем, тахикардии при введении атропина) и необычных реакций (брадикардии при введении атропина), частота возникновения какого-либо заболевания при некоем воздействии (опухоли при облучении ионизирующей радиацией) или, наоборот, исчезновения этого заболевания при определенном лечении (к примеру, уменьшение числа колоний опухоли Раушенбаха в печени мышей после внутривенного введения перфторана). В опытной группе погибли все 3 животных, в группе контроля из 9 животных ни одно не погибло. Можно показать, что различия между группами статистически не значимы (p > 0,05). Различия становятся достоверными, если в контроле из 10 животных ни одно не погибло. То есть если в опытной группе погибли все 3 животных, то минимальный объем выборки, чтобы различия между опытом и контролем были достоверны, равен как минимум 13 животных.
В медицинских исследованиях итоговые данные о количестве наблюдений этих градаций признаков в группах больных – частоты или численности nij сводятся в многопольные таблицы сопряженности. В строках таблиц, как правило, описаны группы, сформированные в зависимости от использованных методов лечения, лекарственных препаратов и т.д. В столбцах представлены возможные уровни признаков, обусловленные различными результатами лечения – исходы лечения. Каждая ячейка таблицы стоит на пересечении столбца и строки. В результате каждая ячейка содержит комбинацию значений двух переменных (очевидно, поэтому эти таблицы называются таблицами сопряженности).
Самыми простыми перекрестными табуляциями являются четырехклеточные таблицы с 2 строками и 2 столбцами – так называемые таблицы сопряженности 2х2 (табл. 1). Эти таблицы являются частым способом представления статистических данных при клинических исследованиях по качественным показателям (значительное число результатов клинических наблюдений являются не количественными, а качественными). Нетрудно видеть, что они соответствуют частному случаю номинальных бинарных шкал, то есть состоящих из двух градаций признаков по типу «да – нет» (например, наличие – отсутствие эффекта от лечения) в двух группах больных общим числом N = n11 + n12 + n21 + n22.
Таблица 1
Общий вид таблиц сопряженности 2х2
|
В |
не В |
||
|
А |
n11 |
n12 |
|
|
не А |
n21 |
n22 |
Таблицы сопряженности позволяют решить следующие задачи:
1) проанализировать эмпирические частоты наблюдений градаций исследуемых признаков в группах пациентов, подвергнутых различным вмешательствам, и определить наличие или отсутствие «терапевтической пользы»;
2) исследовать степень доверия к установленным различиям (статистическую значимость различий), а именно принять или опровергнуть нулевую гипотезу H0 об отсутствии влияния данного хирургического метода или проводимой терапии на состояние больного H0: p = p0; H1: p ≠ p0.
При этом сначала традиционно формулируется нулевая гипотеза, то есть изначально предполагается, что исследуемые методы, препараты и пробы не оказывают никакого влияния на результаты лечения и диагностики, а полученные различия между группами больных кажущиеся (случайны). Потом делается попытка опровергнуть нулевую гипотезу с определенной вероятностью и с помощью специальных критериев.
Поскольку речь идет о случайных событиях (на самочувствие больных всегда оказывает влияние множество факторов, как улучшающих, так и ухудшающих его состояние, и учесть все врачу никогда не представляется возможным), заключения проведенного исследования могут носить лишь вероятностный характер. Никакой статистический критерий не дает исследователю абсолютной уверенности в различии результатов лечения между группами или их идентичности. Другими словами, утверждения об эффективности лечения при использовании того или иного метода лечения или лекарственного препарата могут высказываться только с определенной вероятностью (0,95; 0,99 или 0,999 как это обычно принято в статистических исследованиях или на определенном уровне значимости 0,05; 0,01 или 0,001 соответственно).
Точный метод Фишера (ТМФ) достоверности наблюдаемых различий, как следует из его названия, является точным и может использоваться независимо от особенностей выборки. Он принадлежит к непараметрическим статистическим методам и основан на переборе всех возможных вариантов заполнения таблицы при фиксированных значениях маргинальных частот, что позволяет получать точные значения вероятности событий, столь же или еще менее вероятных, чем те, которые наблюдались в действительности. После этого делается вывод о том, достаточны ли различия в сравниваемых группах по величине, чтобы считать их статистически значимыми (другими словами, есть ли связь между результатами и примененными способами лечения).
Цель исследования
Итак, зададимся вопросом, какие различия должны быть в значениях частот nij, чтобы можно было достоверно заявлять, что различия в результатах лечения достоверны, связаны с применением новых методов лечения и новых лекарственных средств и не связаны со случайными причинами? Какова должна быть минимальная численность выборки пациентов (наблюдений) N = n11 + n12 + n21 + n22, чтобы иметь основания утверждать о преимуществе одного способа лечения (хирургического, терапевтического) над другим?
Методы исследования
На первый вопрос дает ответ, например, критерий хи-квадрат, а для малочисленных выборок – точный метод Фишера [1]. Именно ТМФ применен в данном исследовании.
Результаты исследования и их обсуждение
Чтобы ответить на второй вопрос, нужно рассмотреть наиболее «выгодные» варианты, например таблицы сопряженности 2х2, у которых n12 = n21 = 0. Будем называть такие таблицы наиболее перекошенными. Для наиболее перекошенных таблиц объем выборки N = n11 + n12 + n21 + n22 = n11 + + n22 будет минимальным.
Также для определенности предположим, что метод или лекарство, примененные в одной группе (пусть это будет Группа 1), приносят успех, а метод или лекарство, использованные в другой группе (Группа 2), – неуспех (табл. 2). Таким образом, будем рассматривать благоприятные ( ) исходы в Группе 1 и неблагоприятные (
) исходы в Группе 1 и неблагоприятные ( ) исходы в Группе 2. В качестве Успеха предположим, как это принято, успешный исход лечения, отсутствие боли при вмешательстве или осложнений после проведенного лечения, повышение индекса качества жизни и т.д. В качестве Неудачи – соответствующие противоположные исходы.
) исходы в Группе 2. В качестве Успеха предположим, как это принято, успешный исход лечения, отсутствие боли при вмешательстве или осложнений после проведенного лечения, повышение индекса качества жизни и т.д. В качестве Неудачи – соответствующие противоположные исходы.
Таблица 2
Пример наиболее перекошенной таблицы сопряженности 2х2
|
Успех |
Неудача |
||
|
Группа 1 |
n11 |
0 |
|
|
Группа 2 |
0 |
n22 |
Упростим обозначения. Пусть n11 = n1, а n22 = n2, как в табл. 3. Тогда N = n1 + n2.
Таблица 3
|
Успех |
Неудача |
||
|
Группа 1 |
n1 |
0 |
|
|
Группа 2 |
0 |
n2 |
Для определения статистической значимости полученных в результатах лечения различий можем применить прямой расчет гипергеометрических вероятностей, лежащих в основе точного метода Фишера. Так вероятность реализации табл. 3 будет равна
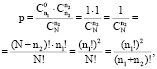
где 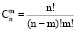 – число сочетаний,
– число сочетаний, 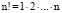 – n-факториал,
– n-факториал, 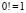 .
.
Поскольку рассматриваемые таблицы являются максимально перекошенными, то соответствующие им гипергеометрические вероятности можно просто сравнить с принятым для анализа уровнем значимости (в противном случае нужно еще учитывать таблицы с теми же маргинальными частотами, но меньшими вероятностями их реализации). Можно также применить ряд статистических мини-программ [2] или универсальные пакеты типа «Statistica», «умеющие» работать с таблицами сопряженности [3]. Решение этих несложных задач максимально облегчается, если есть возможность воспользоваться заранее вычисленными таблицами В.С. Генеса [4] или В.Д. Брицкого [5].
Последовательно по мере возрастания n1 рассмотрим частные случаи.
1. В результате проведенного в группах лечения нет благоприятных исходов в Группе 1 (n1 = 0). Учтем, что для метода Фишера нет ограничений даже в том случае, если число больных с неким значением признака равно нулю (одно из значений n в ячейке равно 0). В этом случае применение ТМФ дает результат, согласно которому нет оснований говорить об эффективности лечения в Группе 1, даже если число неблагоприятных исходов в Группе 2 очень велико: n2 = N и 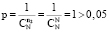 независимо от численного значения n2.
независимо от численного значения n2.
2. Один больной в Группе 1 (n1 = 1). При n1 = 1, как показывает программа статистических вычислений «Точный критерий Фишера» (рис. 1), значимость различий между группами наступает только при n2>18, то есть начиная с таблиц, у которых n2 = 19 (табл. 4, 4а). Это соответствует числу больных в Группе 2 равным минимально 19 (!). В этом случае общее число больных в обеих группах, которое требуется для выявления эффективности одного метода лечения или лекарственного средства над другим методом или средством, равно N = 1 + 19 = 20 (рис. 3). Кстати, аналогичное значение N дает прямой расчет гипергеометрической вероятности: 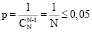 , откуда
, откуда 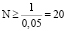 .
.
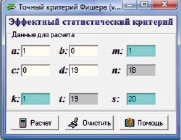
Рис. 1. Мини-программа статистических вычислений «Точный критерий Фишера»
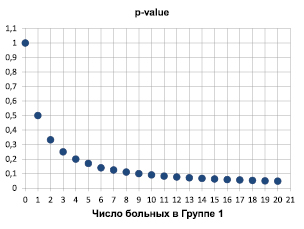
Рис. 2. Величина p-value в зависимости от числа больных в Группе 1
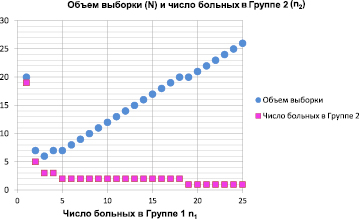
Рис. 3. Зависимость минимального числа больных в двух группах (объем выборки N) в зависимости от числа больных в Группе 1 (с благоприятными исходами), когда, в принципе, возможно установить статистически значимые различия в результатах лечения на уровне значимости 0,05
Таблица 4
Таблица сопряженности 2х2 при n1 = 1 и n2 = 19, когда установленные различия между группами при n1 = 1 становятся значимыми
|
Успех |
Неудача |
||
|
Группа 1 |
1 |
0 |
|
|
Группа 2 |
0 |
19 |
Таблица 4а
|
Успех |
Неудача |
|
|
Группа 1 |
|
– |
|
Группа 2 |
– |
|
Как известно, p-value (p-значение) – величина, применяемая при статистической проверке гипотез: p-value – наименьшая величина уровня значимости, при котором событие можно считать неслучайным. Расчет p-value является обратным процедуре проверки нулевой гипотезы H0. Расчет величины p-value [6] подтверждает выполненные вычисления N (рис. 2). Из рисунка видно, что p-значение становится меньше 0,05 только при n1 > 18.
3. Двое больных в Группе 1 (n1 = 2). Анализ различий между группами с помощью таблиц [2] или программы «Точный критерий Фишера» в этом случае даёт основания утверждать, что они становятся статистически значимыми уже при n2 = 5. Таким образом, при числе больных с благоприятным исходом в Группе 1 равным 2 и числе больных с неблагоприятным исходом в Группе 2 равным 5 (табл. 5, 5а) нулевая гипотеза H0 может быть отвергнута и принята альтернативная гипотеза H1. Численность выборки в этом случае N = 2 + 5 = 7 (рис. 2).
Таблица 5
Таблица сопряженности 2х2 при n1 = 2 и n2 = 5, когда различия между группами при n1 = 2 становятся значимыми
|
Успех |
Неудача |
||
|
Группа 1 |
2 |
0 |
|
|
Группа 2 |
0 |
5 |
Таблица 5а
|
Успех |
Неудача |
|
|
Группа 1 |
|
– |
|
Группа 2 |
– |
|
Таким образом, увеличение n1 от 1 до 2 ведет к резкому снижению n2 и, соответственно, минимальной численности больных, при которой различия в группах можно считать значимыми.
4. Трое больных в Группе 1 (n1 = 3). В этом случае в Группе 2 должно быть зарегистрировано не менее трех больных с неблагоприятным исходом из трех (табл. 6). Общая сумма больных в обеих группах здесь N = 3 + 3 = 6, то есть меньше, чем в предыдущем рассмотрении.
Таблица 6
Таблица сопряженности 2х2 при n1 = 3 и n2 = 3, когда различия между группами становятся значимыми
|
Успех |
Неудача |
||
|
Группа 1 |
3 |
0 |
|
|
Группа 2 |
0 |
3 |
Таблица 6а
|
Успех |
Неудача |
|
|
Группа 1 |
|
– |
|
Группа 2 |
– |
|
На самом деле, подсчитаем гипергеометрическую вероятность при n1 = n2 = 3 (вероятность наблюдения табл. 6).
Вероятность наблюдения этой таблицы равна 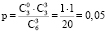 . Поскольку таблица является наиболее перекошенной из всех возможных таблиц (с данным набором маргинальных частот), то полученное значение вероятности 0,05 и есть то p-значение, которое фигурирует в точном методе Фишера и которое сравнивается с 0,05. Как видно, оно не больше 0,05, поэтому есть достаточные основания отвергнуть нулевую гипотезу (об отсутствии различий в группах) и принять альтернативную гипотезу о связи результатов лечения с применением того или иного метода лечения или лекарственного средства.
. Поскольку таблица является наиболее перекошенной из всех возможных таблиц (с данным набором маргинальных частот), то полученное значение вероятности 0,05 и есть то p-значение, которое фигурирует в точном методе Фишера и которое сравнивается с 0,05. Как видно, оно не больше 0,05, поэтому есть достаточные основания отвергнуть нулевую гипотезу (об отсутствии различий в группах) и принять альтернативную гипотезу о связи результатов лечения с применением того или иного метода лечения или лекарственного средства.
5. Дальнейший анализ при n1 = 4 и n1 = 5 показывает, что минимальный объем выборки больных равен 7, причем начиная с n1 = 5 становится равным n1 + 2, а при n1 > 18 – сумме n1 + 1 (табл. 7, рис. 3).
Таблица 7
|
Число больных в Группе 1 n1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
Объем выборки N = n1 + n2 |
20 |
7 |
6 |
7 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
20 |
21 |
22 |
23 |
24 |
25 |
|
Число больных в Группе 2 n2 |
19 |
5 |
3 |
3 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
1 |
1 |
1 |
В заключение отметим, что при любых других вариантах таблиц сопряженности, менее перекошенных, чем рассмотренные (табл. 2), но с теми же маргинальными частотами, минимальное число больных будет заведомо большим. Всего для малочисленных выборок (N ≤ 10) возможны следующие варианты, когда результаты лечения в первой группе «лучше» и различия достоверны (табл. 8).
Таблица 8
|
Общее число больных в группах, N |
Варианты таблиц сопряженности 2х2, когда различия в группах достоверны (p ≤ 0,05) |
|
1 |
– |
|
2 |
– |
|
3 |
– |
|
4 |
– |
|
5 |
– |
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
Как видно, не все варианты в таблице представлены максимально перекошенными таблицами. Число вариантов, когда различия достоверны, может быть увеличено путем изменения порядка следования строк или столбцов, а также заменой строк на столбцы (транспонированием).
Выводы
Таким образом, при n1 = 0 не может быть никаких оснований утверждать, что метод лечения, примененный в Группе 1, более эффективен, чем метод в Группе 2, даже при очень большом числе неблагоприятных исходов в Группе 2 (рис. 3). Случай n1 = 1, когда в Группе 1 только один больной (с благоприятным исходом), также отбрасываем. В этом случае необходимо иметь 19 больных в Группе 2 и все (!) – с неблагоприятным исходом, то есть комбинацию: 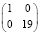 . Только тогда на уровне значимости 0,05 можно утверждать, что лечение больных в Группе 1 эффективнее, чем в другой группе. Объем выборки здесь достаточно большой – 20 больных.
. Только тогда на уровне значимости 0,05 можно утверждать, что лечение больных в Группе 1 эффективнее, чем в другой группе. Объем выборки здесь достаточно большой – 20 больных.
Дальнейший анализ наименьшего числа наблюдений, когда возможно статистически значимо утверждать, что между группами больных есть существенные различия и что один метод лечения или лекарственное средство эффективнее другого, показал, что наименьшее число больных в обеих группах должно быть не менее 6.
При этом распределение больных по группам и исходам может быть таким как в табл. 6, то есть 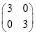 или
или 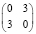 .
.
Библиографическая ссылка
Муслов С.А., Маев И.В., Салманов П.Л., Лапшихина Е.А. ЕЩЁ РАЗ О МИНИМАЛЬНОМ ЧИСЛЕ БОЛЬНЫХ В КАЖДОЙ ГРУППЕ ДЛЯ ВКЛЮЧЕНИЯ В ИСПЫТАНИЕ // Международный журнал прикладных и фундаментальных исследований. 2018. № 1. С. 77-83;URL: https://applied-research.ru/ru/article/view?id=12069 (дата обращения: 22.12.2025).