Расчет теплопроводности непрерывно неоднородных тел является новым направлением в физике твердых тел. В большинстве случаев подобные задачи решаются для слоистых тел классическими методами [1].
При решении одномерных задач для неоднородных тел в цилиндрических и сферических координатах уравнения методы решения и результаты во многом подобны [2]. При решении задачи теплопроводности неоднородных тел, эту закономерность можно распространить и на условно бесконечные пластины, разделяющих разные среды. В данной работе эти задачи объединены путем применения к их решению единого подхода.
Дифференциальное уравнение теплопроводности имеет вид
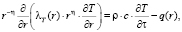 (1)
(1)
где r – ось направленная перпендикулярно плоскости рассматриваемого тела; η – указатель системы координат: 0 – декартовая; 1 – цилиндрическая; η = 2 – сферическая; r – объемный вес, кг/м3; с – удельная теплоемкость, Дж/(кг °С); в данной работе в отличие от [3] q(r) зависит от интенсивности внутренних источников тепловыделений, от воздействия химических реакций, от внутреннего трения, от радиационного поля, от прохождения электрического тока и др.; λT(r) – коэффициент теплопроводности, Вт/(м °С). Для различных тел λT(r) может возрастать, так и уменьшаться при увеличении температуры. Твердые тела уменьшают коэффициент теплопроводности. Коэффициент теплопроводности газов также зависит и от давления [1].
Во многих случаях ограждающие конструкции бывают конструктивно неоднородными, слоистыми. Например, в жилых застройках часто встречаются пласты: декоративный, ограждающий, теплоизоляционный, облицовочный и т.д. В данной постановке коэффициент теплопроводности имеет непрерывную неоднородность.
Аналитические решения
Пусть 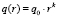 ,
, 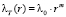 .
.
Рассматривается стационарная задача теплопроводности, т.е. 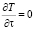 . Тогда уравнение (1) приобретает вид
. Тогда уравнение (1) приобретает вид
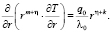 (2)
(2)
Интегрируя (1) по r, получим
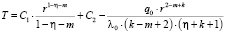 ; (3)
; (3)
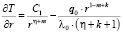 , (4)
, (4)
где С1 и С2 – произвольные постоянные.
Граничные условия 1 рода.
Заданы законы размещения температуры на поверхности тела:
r = a, T = Ta; r = b, T = Tb; (5)
Подставляя в (3), получим
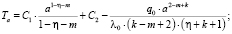
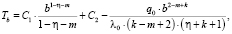 (6)
(6)
Коэффициенты С1 и С2 определяются из решений систем уравнений (6):
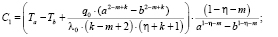
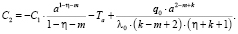 (7)
(7)
Граничные условия 2 рода.
Заданы законы распределения интенсивности теплового потока g на границах:
r = a, 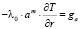 ; r = b,
; r = b, 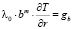 ; (8)
; (8)
Подставляя в (4), получим
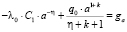 ;
; 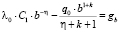 . (9)
. (9)
Граничные условия 3 рода.
Заданы законы конвективного теплообмена среды с поверхностью тела. Применяются в задачах при обтекании поверхности тела жидкостью или газом [1]:
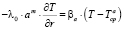 ;
; 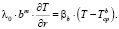 (10)
(10)
Здесь βа, βb – коэффициенты теплоотдачи внутренних и внешних поверхностей;
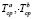 – температура окружающей среды вблизи внутренних и внешних поверхностей.
– температура окружающей среды вблизи внутренних и внешних поверхностей.
Знак минус ставится, когда направление внешней нормали, рассматриваемой поверхности и оси r не совпадают.
Преобразуем граничные условия (9) в виде
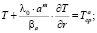
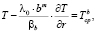 (11)
(11)
и подставляем в (11) решение (3) и (4), тогда решение уравнения (1) определяется из решения системы уравнений
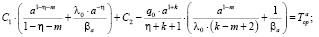
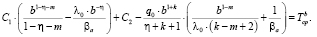 (12)
(12)
При надобности, для описания различных сложных теплофизических процессов, можно составлять произвольные комбинации сумм граничных условий (5), (8) и (11). Из полученных систем уравнений определяются коэффициенты С1 и С2.
Граничные условия 4 рода.
Применяются в конструкциях, состоящих из различных слоев. В контакте любых двух слоев тел температура и интенсивность тепловых потоков равны:
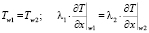 , (13)
, (13)
где w1 и w2 – условные обозначения контактируемых двух тел. В данной постановке граничные условия четвертого рода не рассматриваются из-за непрерывной неоднородности рассматриваемого тела.
Полученные решения (12) имеют особые случаи при: m = 1 – η, m = k + 2 и k + η = –1.
Рассмотрим m = 1 – η: η = 0, m = 1, η = 1, m = 0 и η = 2, m = –1.
При η = 0, m = 1 уравнение (2) имеет вид
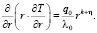 (14)
(14)
Интеграл уравнения (14) для всех случаев m = 1 – η имеет вид:
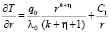 ;
;
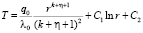 , (15)
, (15)
где C1 и C2 – произвольные постоянные.
При k + η = –1 имеются следующие альтернативы:
η = 0, k = –1, m = 1, η = 1, k = –2, m = 0, η = 2, k = –3, m = –1.
Для всех случаев k + η = –1 уравнение (14) имеет вид
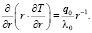 (16)
(16)
Интеграл уравнения (14) имеет вид
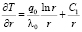 ;
;
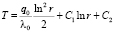 , (17)
, (17)
где C1 и C2 – произвольные постоянные.
Рассмотрим m = k + 2. Количество таких вариантов может быть большим. Но частные случаи, когда тело однородное при m = 0, k = –2 и k = 0, m = 2 соответствует случаю (16) и решению (17). При других значениях m и k соответствует случаю (14) и решению (15).
На рис. 1 представлена эпюра распределения температуры в сечений цилиндрического железобетонного радиaционно-теплового экрана АЭС. Экран устанавливается за корпусом реактора и предназначен для снижения радиационных и тепловых воздействий, генерирующихся при работе атомного реактора, на находящиеся за ним строительные конструкции биологической защиты. Задача решена при различных вариантах неоднородности железобетона и значений внутренних источников тепла, обусловленных воздействием потока нейтронов при k = 0, q0 = ± 1000 Bт/м3 и следующих исходных данных: a = 1 м, b = 2 м, Ta = –40 °С, Tb = 20 °С, ba = bb = 35 Вт/(м2 °С). Граничные условия 3 рода.
Для решения сформулированной краевой задачи (1) вариационно-разностным методом. Тогда эквивалентный функционал метода Ритца [4] имеет вид
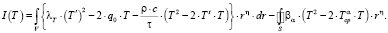 (18)
(18)
Cистема алгебраических уравнений решена методом прогонки [5].
В табл. 1 показаны результаты численного и аналитического решений стационарной задачи при граничных условиях 3 рода в неоднородном теле (m = –1) при наличии внутренних источников тепловыделений при k = 0, q0 = 1000 Вт/м3 [2], a = 1 м, b = 2 м, Ta = –40 °С, Tb = 20 °С, βa = βb = 35 Вт/(м2 °С) [4].
Результаты численного расчета при разбиении толщины стенки на 10 интервалов практически совпадают с аналитическим решением (табл. 1). Для оценки зависимости коэффициента теплопроводности от температуры рассмотрена задача при a = 1 м, b = 2 м, Ta = –40 °С, Tb = 20 °С, βa = βb = 35 Вт м2 °С. Граничные условия 3 рода. Функция, аппроксимирующая график неоднородности жаростойкого бетона В30 [6] λ(T) = 3 – 0,007 T Вт/(м °С) [3].
Коэффициенты λ0 и m, используемые при аналитических решениях, определяются из граничных условий:
r = a, 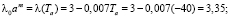
r = b, 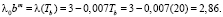
Откуда
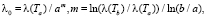
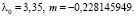
При необходимости аналогично можно получить формулу для определения k:
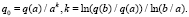
Решение получено при разбиении толщины стенки на 10 интервалов.
На рис. 2 показаны эпюры стационарного температурного поля в бетонном неоднородном теле для 3 итерации (табл. 2). Например, решения для шара обозначены как «Шар», «Ш-1» и «Ш-2». Решения в последних шагах практически совпадают.
На рис. 3 изображены эпюры нестационарного теплового поля в бетонном неоднородном теле через час, день и месяц (31 дней). Бетон имеет следующие теплофизические параметры λT(T) = 3 – 0,007 T Вт/(м °С), ρ = 2500 кг/м3, с = 920 Дж/(кг °C) и связаны с внешней средой (βa = 35 Вт/(м2 °С), βb = 35 Вт/(м2 °С), Tb = 20 °С). В начальный момент времени температура во всем теле равна 20 °С, нестационарный процесс начинается, когда на внутренней части температура среды установлена Ta = –40 °С. Использованы граничные условия третьего рода.
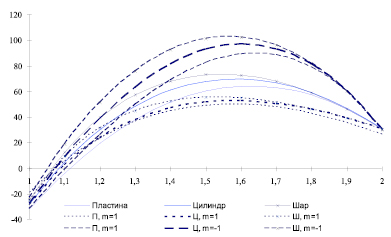
Рис. 1. Распределение температуры в неоднородном теле с внутренним источником тепловыделений q0 = 1000Bт/м3 при различных вариантах неоднородности: m = 0 и m = ± 1
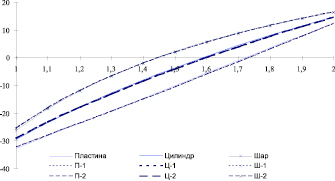
Рис. 2. Решение нелинейной задачи теплопроводности
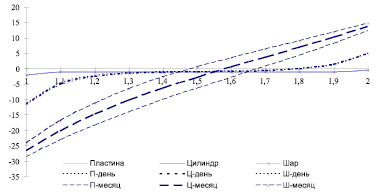
Рис. 3. Решение нелинейной нестационарной задачи теплопроводности
Таблица 1
Результаты численного и аналитического решений стационарной задачи при граничных условиях 3 рода
|
R, м |
Пластина |
Цилиндр |
Шар |
Пластина |
Цилиндр |
Шар |
Пластина |
Цилиндр |
Шар |
|
аналитика |
аналитика |
аналитика |
численный |
численный |
численный |
разница |
разница |
разница |
|
|
1 |
–22,07 |
–18,11 |
–13,76 |
–22,08 |
–18,15 |
–13,83 |
0,01 % |
0,04 % |
0,07 % |
|
1,1 |
7,47 |
16,75 |
26,5 |
7,42 |
16,72 |
26,41 |
0,05 % |
0,03 % |
0,09 % |
|
1,2 |
34,23 |
46,25 |
58,12 |
34,15 |
46,22 |
58,02 |
0,08 % |
0,03 % |
0,09 % |
|
1,3 |
57,21 |
69,89 |
81,58 |
57,11 |
69,86 |
81,47 |
0,09 % |
0,03 % |
0,10 % |
|
1,4 |
75,45 |
87,19 |
97,19 |
75,35 |
87,17 |
97,09 |
0,09 % |
0,02 % |
0,09 % |
|
1,5 |
87,97 |
97,65 |
105,12 |
87,87 |
97,64 |
105,03 |
0,09 % |
0,01 % |
0,09 % |
|
1,6 |
93,8 |
100,81 |
105,45 |
93,71 |
100,8 |
105,38 |
0,09 % |
0,01 % |
0,07 % |
|
1,7 |
91,95 |
96,15 |
98,19 |
91,88 |
96,15 |
98,14 |
0,07 % |
0,00 % |
0,05 % |
|
1,8 |
81,46 |
83,21 |
83,28 |
81,42 |
83,21 |
83,25 |
0,04 % |
0,00 % |
0,03 % |
|
1,9 |
61,35 |
61,48 |
60,63 |
61,33 |
61,49 |
60,63 |
0,02 % |
0,01 % |
0,00 % |
|
2 |
30,64 |
30,48 |
30,11 |
30,65 |
30,5 |
30,14 |
0,01 % |
0,02 % |
0,03 % |
Таблица 2
Эпюры температуры для 3 итерации
|
R, м |
Пластина |
Цилиндр |
Шар |
П-1 |
Ц-1 |
Ш-1 |
П-2 |
Ц-2 |
Ш-2 |
|
1 |
–32,61 |
–29,55 |
–26,05 |
–32,21 |
–29,05 |
–25,47 |
–32,21 |
–29,04 |
–25,47 |
|
1,1 |
–28,09 |
–23,45 |
–18,32 |
–27,97 |
–23,31 |
–18,17 |
–27,96 |
–23,3 |
–18,16 |
|
1,2 |
–23,57 |
–17,89 |
–11,88 |
–23,69 |
–18,01 |
–11,99 |
–23,67 |
–18 |
–11,98 |
|
1,3 |
–19,04 |
–12,77 |
–6,42 |
–19,36 |
–13,07 |
–6,69 |
–19,35 |
–13,06 |
–6,68 |
|
1,4 |
–14,52 |
–8,04 |
–1,75 |
–14,99 |
–8,45 |
–2,08 |
–14,98 |
–8,44 |
–2,08 |
|
1,5 |
–10 |
–3,62 |
2,31 |
–10,57 |
–4,1 |
1,95 |
–10,56 |
–4,09 |
1,95 |
|
1,6 |
–5,48 |
0,5 |
5,86 |
–6,11 |
0,01 |
5,5 |
–6,1 |
0,01 |
5,51 |
|
1,7 |
–0,96 |
4,38 |
8,99 |
–1,6 |
3,9 |
8,67 |
–1,6 |
3,9 |
8,67 |
|
1,8 |
3,57 |
8,03 |
11,78 |
2,95 |
7,61 |
11,5 |
2,95 |
7,61 |
11,51 |
|
1,9 |
8,09 |
11,49 |
14,27 |
7,56 |
11,14 |
14,06 |
7,56 |
11,14 |
14,06 |
|
2 |
12,61 |
14,77 |
16,51 |
12,21 |
14,52 |
16,37 |
12,21 |
14,52 |
16,37 |
Толщина стенки при a = 1 м, b = 2 м разбита на 10 интервалов. Шаг по времени в каждом рассматриваемом периоде разбит на 100 интервалов: первый час разделен на интервал по 36 сек; оставшиеся 23 часа первого дня по 828 сек; оставшиеся 30 дней месяца по 25920 сек.
Как видно из эпюр температурного поля (рис. 3), в начальный момент времени во всех рассматриваемых телах законы распределения температурного поля по сечению близки и количественно, и качественно. С течением времени решения стремятся к решению стационарных задач (рис. 2).
Исходя из проведенных расчетов, можно сделать заключение о значительном влиянии на температурное поле внутреннего тепла разогрева и неоднородности материала.
В данной работе q(r) является переменной величиной, которая позволит решать задачи химических реакций, радиационного поля, электрического тока и др. Эти решения, при наличии соответствующих коэффициентов, справедливы и для решения задач влагопереноса, диффузии, коррозии и трещинообразования и других задач, описываемых уравнением теплопроводности.
Библиографическая ссылка
Мусабаев Т.Т., Каюпов Т., Сейлханова Д.К. НОВЫЕ МЕТОДЫ РАСЧЕТА НЕЛИНЕЙНЫХ ОДНОМЕРНЫХ ЗАДАЧ ТЕПЛОПРОВОДНОСТИ ДЛЯ ХИМИЧЕСКИ НЕОДНОРОДНЫХ ТЕЛ // Международный журнал прикладных и фундаментальных исследований. 2018. № 2. С. 70-75;URL: https://applied-research.ru/ru/article/view?id=12110 (дата обращения: 31.12.2025).

