Потребность в новых материалах растёт быстрыми темпами [1, 2]. Эта потребность приводит к созданию новых композитных материалов. Также эта потребность достаточно часто имеет противоречивые требования к свойствам новых материалов. Здесь под противоречивыми требованиями к свойствам новых материалов понимаются требования, которые невозможно реализовать одновременно. Одним из самых распространённых противоречивых требований к свойствам новых материалов является требование обеспечения максимального значения конкретного свойства нового материала (например, прочности) и обеспечения минимальной стоимости нового материала. Часто встречаются противоречивые требования к конкретным свойствам материала (например, максимальная твёрдость и максимальная вязкость материала).
Для удовлетворения этих противоречивых требований используется многокритериальная оптимизация. Имеются следующие методы многокритериальной оптимизации: ранжирования критериев, последовательных уступок, идеальной точки, свёртывания векторного критерия в суперкритерий, ограничений, справедливого компромисса, равномерной оптимизации, интерактивный, генетический [3, 4].
Метод ранжирования критериев упорядочивает критерии по важности. Далее решается задача поиска максимума F1, потом решается задача поиска максимума F2 при условии максимума F1, и так далее. В итоге решается задача поиска максимума FN при условии максимума F1,…,FN-1.
Метод последовательных уступок упорядочивает критерии по важности. Далее решается задача поиска максимума F1 и назначается уступка U1, потом решается задача поиска максимума F2 при условии, что значение F1 не меньше, чем maxF1-U1, и назначается уступка U2 и так далее. В итоге решается задача поиска максимума FN при условии FI ≥ max FI – UI, I = 1, N – 1.
Метод идеальной точки устанавливает максимальные значения по всем критериям, и потом определяется точка, минимально удалённая от точки с максимальными значениями по всем критериям.
Метод свёртывания векторного критерия в суперкритерий сводит многокритериальную задачу оптимизации к однокритериальной задаче оптимизации посредством определения весовых коэффициентов для каждого критерия и последующим поиском максимума суперкритерия, полученного суммированием критериев, умноженных на весовые коэффициенты.
Метод ограничений определяет главный критерий. Далее решается задача поиска максимума главного критерия, а остальные критерии используются как ограничения.
Метод справедливого компромисса базируется на том, что относительное ухудшение одного или нескольких критериев не превосходит относительного улучшения по остальным критериям. Решается задача поиска максимума произведений всех критериев.
В методе равномерной оптимизации все критерии считаются равнозначными и решается задача поиска максимума суммы всех критериев.
В интерактивном методе решение задачи многокритериальной оптимизации осуществляется с участием эксперта или группы экспертов, которые принимают решения на основе своих знаний и информации полученной от системы поддержки принятия решений.
В генетическом методе используются механизмы естественного отбора, такие как наследование, мутации, отбор, кроссинговер.
Для ускорения создания новых композитных материалов с противоречивыми требованиями к их свойствам создана программа выбора оптимального состава шихты для изготовления композитной заготовки.
На основе этой программы будет создана экспертная система программы выбора оптимального состава шихты для изготовления композитной заготовки [5]. Структура экспертной системы показана на рис. 1.
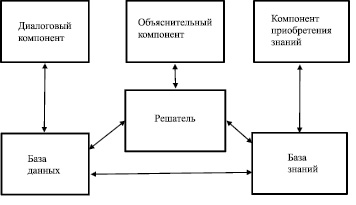
Рис. 1. Структура экспертной системы
Решатель берёт исходные данные из базы данных и использует знания из базы знаний для обработки исходных данных и решения задачи.
База данных содержит данные задач. Данные каждой задачи содержат исходные данные задачи и могут содержать решение задачи.
База знаний содержит знания необходимые для решения определённых задач.
Компонент приобретения знаний обеспечивает наполнение базы знаний в диалоге с экспертом.
Объяснительный компонент комментирует, как было получено решение. Это необходимо для проверки решения.
Диалоговый компонент обеспечивает взаимодействие пользователя и экспертной системы.
Алгоритм программы
Выбор оптимального состава шихты на основе поиска максимума обобщённого критерия делается по следующему алгоритму:
1. Нормирование экспериментальных данных критериев оптимизации.
Нормирование осуществляется по следующей формуле:
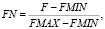
где FN – нормированное значение критерия оптимизации, F – значение критерия оптимизации, FMAX, FMIN – соответственно максимальные и минимальные значения критерия оптимизации.
2. Определение функций критериев оптимизации по нормированным экспериментальным данным.
Функция критерия оптимизации определяется методом наименьших квадратов в виде
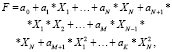
где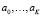 
– коэффициенты, 
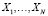– варьируемые факторы.
3. Определение функции обобщённого критерия оптимизации.
Функция обобщённого критерия оптимизации определяется по формуле
,
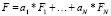где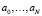 
– коэффициенты, 
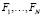– критерии оптимизации.
4. Определение максимума функции обобщённого критерия оптимизации [6].
В некоторых ситуациях возможна взаимная компенсация критериев оптимизации, и тогда не удаётся получить оптимальное решение поиском максимума обобщённого критерия. Возможны следующие варианты преодоления этой проблемы: увеличение или уменьшение количества экспериментов или критериев оптимизации, изменение порядка полинома на 2 шаге алгоритма, изменение коэффициентов на 3 шаге алгоритма, использование другого метода оптимизации.
Алгоритм выбора оптимального состава шихты на основе критерия Парето представлен на рис. 2 [7].
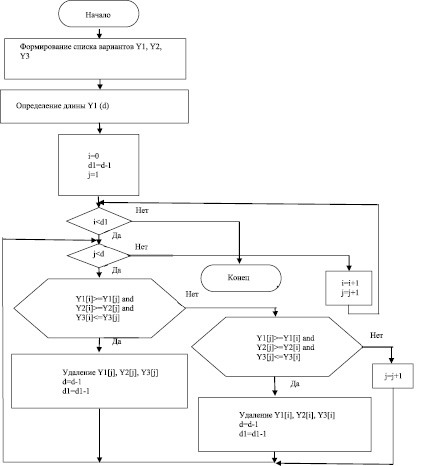
Рис. 2. Алгоритм выбора оптимального состава шихты на основе критерия Парето
Вектор решения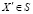 
называется оптимальным по Парето, если не существует 
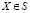такого, что 
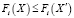для всех i = 1,…, k и 
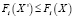для хотя бы одного i.
Бывают случаи, когда на основе критерия Парето не удаётся получить оптимальное решение. Возможны следующие варианты преодоления этой проблемы: увеличение или уменьшение количества экспериментов или критериев оптимизации, использование другого метода оптимизации.
Для того чтобы решить задачу многокритериальной оптимизации иногда приходится использовать несколько методов многокритериальной оптимизации.
Интерфейс программы
Программа создана в IDLE Python 2.7.13 в операционной системе Microsoft Windows XP. На рис. 3 показан интерфейс программы.
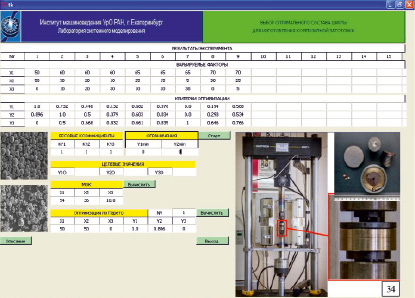
Рис. 3. Интерфейс программы и пример работы программы
Результаты экспериментов заносятся в две таблицы. В таблицу ВАРЬИРУЕМЫЕ ФАКТОРЫ заносятся значения процентного содержания по массе варьируемых факторов X1, X2, X3. В таблицу КРИТЕРИИ ОПТИМИЗАЦИИ заносятся значения критериев оптимизации Y1, Y2, Y3. Количество экспериментов не более 15. После нажатия на клавишу Старт в таблицах появятся результаты экспериментов уплотнения смеси порошка, полученного из сплава ВТ-22 распылением плазмой, с добавками порошка титана ПТМ-1, полученного гидридно-кальциевым способом, порошка сплава никель – алюминий ПВ-Н70Ю30.
В программе имеется возможность выбора оптимального состава шихты для изготовления композитной заготовки двумя способами. Первый способ на основе поиска максимума обобщённого критерия. После нажатия клавиши «Вычислить» у таблицы МОК в этой таблице появятся оптимальные значения варьируемых факторов X1, X2, X3, полученные первым способом. Также появится график обобщённого критерия в зависимости от факторов X1, X2. Второй способ на основе критерия Парето. После нажатия клавиши «Вычислить» у таблицы «Оптимизация по Парето» в этой таблице появятся оптимальные значения варьируемых факторов X1, X2, X3, полученные вторым способом, соответствующие им значения критериев оптимизации Y1, Y2, Y3, номер соответствующего опыта.
Перед вычислением нужно указать весовые коэффициенты KY1, KY2, KY3 для критериев оптимизации Y1, Y2, Y3 в таблице ВЕСОВЫЕ КОЭФФИЦИЕНТЫ, ограничения Y1min, Y2min для критериев оптимизации Y1, Y2 в таблице ОГРАНИЧЕНИЯ.
Перед вычислением могут быть указаны желаемые значения Y1O, Y2O, Y3O критериев оптимизации Y1, Y2, Y3 в таблице ЦЕЛЕВЫЕ ЗНАЧЕНИЯ. Если эти значения указаны, то вычисляются оптимальные значения варьируемых факторов X1, X2, X3, при которых критерии оптимизации Y1, Y2, Y3 находятся на минимальном расстоянии от этих значений.
После нажатия клавиши «Описание» появляется описание возможностей программы. После нажатия клавиши «Выход» программа заканчивает работу.
На рис. 3 показан пример работы программы.
На рис. 4 показан график обобщённого критерия в зависимости от факторов X1, X2, для примера рис. 3.
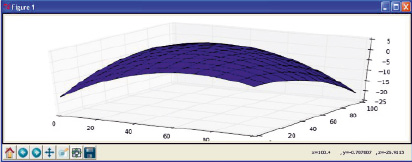
Рис. 4. График обобщённого критерия в зависимости от факторов X1, X2, для примера рис. 3
В экспертной системе, частью которой будет данная программа, предполагается поиск в интернете методов оптимизации и другой необходимой информации. Пользователь может запросить выполнить оптимизацию методом, которого нет в экспертной системе. В этом случае система выдаст соответствующий запрос в поисковую систему. Поисковая система выдаст несколько ответов. Экспертная система выберет нужную информацию из этих ответов и создаст программные средства для оптимизации запрошенным методом. Далее экспертная система выполнит оптимизацию запрошенным методом.
Заключение
Представлена программа выбора оптимального состава шихты для изготовления композитной заготовки. Этот выбор можно сделать следующими способами: на основе поиска максимума обобщённого критерия, на основе метода Парето, а также определение оптимального состава шихты, максимально приближенного к желаемому составу шихты. С помощью этой программы был выбран оптимальный состав шихты для изготовления композитной заготовки из порошка, полученного из сплава ВТ-22 распылением плазмой, с добавками порошка титана ПТМ-1, полученного гидридно-кальциевым способом, порошка сплава никель – алюминий ПВ-Н70Ю30.
Выбор оптимального состава шихты посредством метода поиска максимума обобщённого критерия даёт более точное решение, чем методом Парето, так как методом поиска максимума обобщённого критерия выбор оптимального состава шихты осуществляется на функции, а методом Парето – на числах. При этом оптимальный состав шихты, полученный методом поиска максимума обобщённого критерия, требует подтверждения на опыте, если оптимальный состав не совпадает с экспериментальными данными. А оптимальный состав шихты, полученный методом Парето, не требует подтверждения на опыте, так как оптимальный состав шихты совпадает с данными одного из экспериментов.
Иногда бывает необходимо перебрать несколько методов многокритериальной оптимизации для выбора оптимального состава шихты.
Библиографическая ссылка
Титов В.Г., Залазинский А.Г. ПРОГРАММА ДЛЯ ВЫБОРА ОПТИМАЛЬНОГО СОСТАВА ШИХТЫ ДЛЯ ИЗГОТОВЛЕНИЯ КОМПОЗИТНОЙ ЗАГОТОВКИ // Международный журнал прикладных и фундаментальных исследований. – 2018. – № 3. – С. 31-36;URL: https://applied-research.ru/ru/article/view?id=12144 (дата обращения: 21.11.2024).