Феномен многостадийности, присущий многим процессам развития, является достаточно распространенным, если не универсальным. При этом каждое из многостадийных явлений, сопутствующих старению или износу сложной (многосвязной и репарируемой) системы, протекает при случайных воздействиях, случайном разбросе в исходных параметрах и коэффициентах, случайных отклонениях в исходной структуре, при управляющих воздействиях со случайными компонентами [1]. Таким образом, говорить о периодичности в строгом математическом смысле этого слова не следует. Анализ многостадийных явлений, протекающих в условиях износа (старения), опирается на описания, развитые в рамках геронтологии. Геронтология – наука о старческих изменениях живых организмов, которые хорошо представлен различного рода моделями, в частности имитационными [2]. Существует множество теорий старения, в которых общим является признание, что возможности и функции тела человека снижаются по мере старения.
Одной из первых моделей, описывающей процессы старения, является классическая модель Гомпертца – Мейкхама [3, 4]. При этом модели колебательных процессов, протекающих в живых системах, занимают заметное место в работах, посвященных их моделированию. Достаточно распространены математические модели таких физиологических явлений, как возрастные изменения артериального давления, возрастные изменения гормонального регулирования месячных циклов, возрастные изменения цикличности в суточных метаболических процессах и др. [5, 6].
Данная работа посвящена явлению многостадийности, связанной с онтогенетическими событиями и с процессами старения/износа долгоживущей особи, т.е. представителя вида, не «привязанного» онтогенетическими рамками к цикличности суточной (как у бабочки-однодневки) или сезонной (как у отдельных грызунов или, например, насекомых). Для первичных модельных описаний исследуемого явления также допускается существование онтогенетической программы со случайными отклонениями, которая и определяет соответствующие стадии. При разработке математической модели реализуется модульный принцип: для каждого из процессов адаптации, восстановления, защиты и разрушения допускается первичная модель многостадийных изменений при старении [7]. Взаимодействие этих процессов, изменяющихся в соответствии с общими стадиями, или условия формирования стадий при их взаимодействии (или рассогласовании в ходе старения) является на этом этапе сложной задачей, предполагающей отдельное дополнительное исследование.
Одной из первых математических моделей, описывающих явление старения, является модель Гомпертца – Мейкхама, в которой представлено наблюдаемое увеличение смертности с возрастом [8]. Различные вариации и модификации этой модели проводятся и в настоящее время [9]. В 1860 г. У. Мейкхам добавил в существующую модель Б. Гомпертца константу, которая обуславливала влияние внешней среды. Данная модель основана на идее об износе так называемой «жизнеспособности», которая по сути является идеализированной величиной. Такое описание позволяет довольно-таки просто описывать возрастное изменение смертности человека и хорошо укладывается в терминах математических моделей, описываемых дифференциальными уравнениями. Б. Гомпертц рассматривал смертность как величину, обратную жизнеспособности – способности противостоять всей совокупности разрушительных процессов. Приведем решение, полученное Гомпертцем – Мейкхамом:
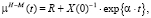(1)
где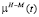 
– уровень смертности, X(0) > 0 – начальный уровень «жизнеспособности», α ≥ 0 – интенсивность износа жизнеспособности, R > 0 – параметр давления среды. Одним из существенных недостатков данной модели является то, что она не отвечает явлению многостадийности старения, которое наблюдается как у живых систем, так и технических объектов.
Материалы и методы исследования
Стоит отметить, что рассмотренное уравнение (1) не учитывает явлений онтогенетических перестроек, которые и обуславливают многостадийность старения. Рассмотрим моменты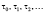 
с τ0 = 0 и 
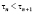для всех n = 0, 1, 2,… такие моменты являются значимыми для развития организма (например, начало периода фертильности). После каждого из таких моментов τn наблюдается период повышенной смертности [8], вызванный дезадаптацией с последующим периодом адаптации. Так момент τ0 будет соответствовать высокой детской смертности, для моментов полового созревания – пик юношеской смертности. Примером служат данные исследования, проведенного в США в 2003 г. [10], на котором явно наблюдаются по крайней мере два из упомянутых здесь подъемов уровня смертности.
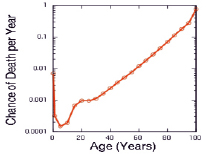
Рис. 1. Функция смертности в США в 2003 г.
Таким образом, целесообразно в рамках механистической расширенной модели износа рассматривать для каждого момента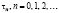 
онтогенетической перестройки инспирированный дезадаптационный подъем уровня смертности 
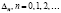с соответствующей скоростью «отладки» 
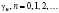. При этом предполагается, что в моменты τn устраняется часть накопленного износа. Однако часть износа остается неустранимой, так же как и компонента давления среды. Следовательно, вместо уравнения (1) целесообразно рассматривать при каждом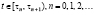 
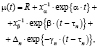(2)
где в правой части равенства первое слагаемое – постоянное давление среды, второе слагаемое – неустранимый (с помощью онтогенетических перестроек) износ (истощение внутренних ресурсов), третье слагаемое – устранимый износ, четвертое слагаемое – привнесенное перестройкой возмущение, устраняемое при отладке.
В соответствии с теоремой Деллашери [11] о семимартингальном разложении процесса с одним скачком, для функции распределения Fτ(t) моментов τ ≥ 0 гибели индивидуумов в популяции с конечной смертностью μ(t) справедливо соотношение
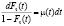. (3)
Для функции дожития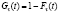 
согласно общей теореме Деллашери 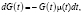[4]:
(4)
с начальным значением G(0) = 1. Решение, очевидно, определяется
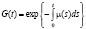, (5)
однако в явном виде имеет непредставимый и малополезный вид (в том числе и из-за стохастичности моментов τn, n = 0, 1, 2,...). Для каждого отдельного индивидуума рассматриваемые моменты τn будут происходить в случайный момент времени, поэтому предполагается, что они являются марковскими моментами, заданными на соответствующем стохастическом базисе.
Для анализа представленной схемы следует прибегнуть к имитационному моделированию. Для этого рассматривается алгоритм численного моделирования в рамках описаний (2) и (3).
Результаты исследования и их обсуждение
Уравнению (4) при численном моделировании соответствует разностная схема с моментами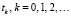 
такими, что t0 = 0, tk+1 – tk = δ при δ ≤ 0,5 и 
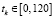(т.е. предполагается анализ индивидуумов в возрасте до 120 лет):
, 
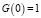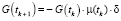, (6)
где μ(tk) при каждом k = 0, 1, 2,… вычисляется по формуле
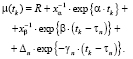(7)
Результат моделирования процесса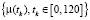 
представлен на рис. 2.
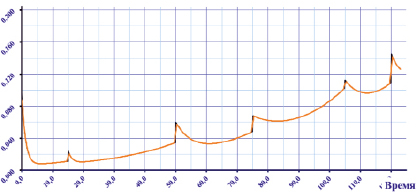
Рис. 2. Зависимость μ(t) от времени (в годах)
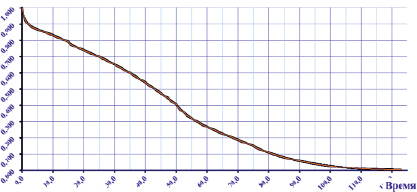
Рис. 3. Зависимость функции дожития G(t) от времени
При моделировании были выбраны следующие параметры: δ = 0,1, R = 1, α = 0,021,Δ0 = 0,09, γ0 = 0,9, Δ1 = 0,012, γ1 = 0,8,Δ2 = 0,015, γ2 = 0,2, Δ3 = 0,08, γ3 = 0,1,Δ4 = 0,06, γ4 = 0,15 и моменты τ0 = 0, τ1 = 15,τ2 = 50, τ3 = 75, τ4 = 105.
При этом осуществлялось равномерное усреднение по пяти ближайшим временным точкам. Соответствующий график функции дожития G(t), реализованный по формуле (6), представлен на рис. 3.
Выводы
Представленная модель представляет собой качественную математическую модель процессов многостадийного старения или износа. В представленной модели было сделано обобщение классической модели Б. Гомпертца (полученной на основе статистических регрессионных моделей, по своей сути фенотипических). Приведена процедура алгоритмизации и обсуждается реализация модели, построенной методами компьютерного имитационного моделирования. Представлены значения параметров математической модели и результаты компьютерного имитационного моделирования.
Физиологические процессы адаптации, восстановления, защиты и разрушения являются основными компонентами при построении простых, но адекватных моделей многостадийного старения или износа. При этом становится возможным объяснить наблюдаемые эпизодические повышения смертности при переходе с одной онтогенетической стадии на следующую. Дальнейшее развитие работы допускает рассмотрение оптимизационных задач и построение стохастических моделей. Значимой задачей оптимизации станет определение оптимальной продолжительности стадии, а также величины уровня метаболизма. Для дальнейшей разработки моделей наряду с различными детерминистскими подходами оказывается продуктивным стохастическое описание. При этом удачным представляется комбинированный семимартингальный подход с «раздельным» представлением отдельных процессов в терминах диффузионных процессов, отдельных – в терминах точечных или мультивариантных процессов, а отдельных – в форме их различного вида сочетаний.
Предложенная и рассмотренная в работе модель в качестве первого блока представляет математическую (базовую, качественную) модель процесса многостадийного износа (старения). Эта базовая, качественная модель восходит к обобщениям качественной модели Б. Гомпертца (построенной на основе статистических регрессионных моделей (фенотипических, по своей сути)). Приведена процедура алгоритмизации и обсуждается имитационная модель, построенная на основе модели качественной. Результаты соответствующего имитационного компьютерного моделирования представлены в виде графиков. Степень адекватности, обеспечивается приблизительно равной – на уровне максимального отклонения времени наступления стадий от статистических демографических показателей – не более 10 % длины стадии, что допустимо укладывается в популяционный разброс самих продолжительностей стадий.
Библиографическая ссылка
Бутов А.А., Коваленко А.А., Шабалин А.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИЗМЕНЕНИЙ В КОМПЕНСАЦИИ ИЗНОСА ПРИ СТАРЕНИИ // Международный журнал прикладных и фундаментальных исследований. – 2018. – № 4. – С. 14-17;URL: https://applied-research.ru/ru/article/view?id=12175 (дата обращения: 23.11.2024).