Развитие современной техники предъявляет все более жесткие требования к современным металлическим сплавам. Подбирая составы для новых металлических сплавов, исследователи изучают физические характеристики, присущие данным сплавам [1–3]. В зависимости от условий эксплуатации, обычно используется один или два физических параметра [4, 5]. В своем исследовании мы решили изучить как можно больше свойств, характеризующих металлические сплавы, и, основываясь на полученных закономерностях, разработать методику, позволяющую прогнозировать изменение физических свойств металлических сплавов при изменении концентрации легирующих элементов или при замене одного легирующего элемента на другой. При таком подходе общая задача разбивается на следующие этапы. Первый – нахождение изменения физических параметров характеризующих металлические сплавы, при изменении концентрации легирующих элементов, и выражение найденных закономерностей в аналитическом виде. Второй – выявление закономерностей, как тот или иной параметр зависит от положения легирующего элемента в периодической системе Д.И. Менделеева.
Необходимо отметить, что, разрабатывая новые сплавы, исследователи вынуждены опираться в основном на экспериментальные данные, ввиду отсутствия теории пригодной для практического использования. Классическая теория, основу которой заложил Френкель, показывает значение теоретической прочности на 2–3 порядка выше, чем реальная прочность [6, 7]. Квантовая теория, в современном ее приложении, является феноменологической [8]. Применяемые в этой теории уравнения включают параметры, значения которых подгоняются под экспериментальные данные [9]. Получается, что они годятся только для данного конкретного случая. При любом изменении, например увеличении концентрации одного из легирующих элементов или примесей [10, 11], входящих в сплав, величины подгоночных параметров изменяются, и их вновь приходится определять из экспериментальных данных.
На данном этапе развития науки большим подспорьем в решении практических задач оказываются диаграммы состояния, которые в свою очередь базируются на экспериментальных данных. Недостатком в использовании этого метода является то, что в основном диаграммы состояния составлены для бинарных сплавов, а на практике используются многокомпонентные сплавы. Учитывая все вышеперечисленные трудности, большинство исследователей подбирает состав сплавов, опираясь на свою интуицию, а не на строгий математический расчет.
Проанализировав состояние современной теории металлических сплавов, мы пришли к выводу, что на данном этапе наиболее рациональной будет разработка такого метода, который позволил бы определять физические характеристики металлических сплавов, опираясь на аналогичные характеристики, присущие сплавам другого состава. То есть мы должны, имея набор физических параметров для ряда однородных сплавов, методом экстраполяции найти эти параметры для сплавов другого состава.
В своем исследовании мы анализировали следующие свойства веществ: твердость по Бринеллю – HB, кг/мм2, твердость по Виккерсу – Hn, кг/мм2, микротвердость – Hm, кг/мм2, относительное удлинение – δ, %, относительное сужение y, %, прочность прочности на растяжение – sв, кг/мм2, предел текучести – st, кг/мм2, модуль нормальной упругости – E, кг/мм2, удельное электросопротивление – r, мкОм/см, теплопроводность – λ, кал/см·с, электропроводность – ρ, См.
Оказалось, что в области твердых растворов все эти величины меняются линейно с ростом концентрации легирующего элемента [12]. Математически это можно описать следующим уравнением:
Y = α + bx, (1)
где Y – величина изучаемого свойства, α и b – коэффициенты, х – концентрация легирующего элемента. Коэффициент α показывает величину исследуемого параметра при нулевой концентрации легирующего элемента, а коэффициент b – быстроту изменения данного параметра при изменении концентрации легирующего элемента. Соответственно, при замене одного легирующего элемента на другой изменяется величина b, а коэффициент α остается неизменным. На графике зависимости свойство – концентрация, для различных легирующих элементов, мы получим набор прямых линий, расходящихся под разными углами из одной общей точки.
Использование коэффициента b вместо уравнения (1) позволяет существенно упростить поиск взаимосвязей между различными физическими свойствами сплавов, так как в этом случае мы будем оперировать набором коэффициентов, а не набором уравнений.
Следующим этапом исследований было выявление зависимости коэффициентов b от положения легирующих элементов в таблице Д.И. Менделеева. Обработав большой массив данных, мы обнаружили, что между коэффициентами bi и номерами групп элементов n (при фиксированном номере периода N) существует взаимосвязь, но она в редких случаях носит линейный характер. В то же время зависимость между коэффициентами bi и номером периода N, для легирующих элементов, принадлежащих к одной группе n, в большинстве случаев была линейной. Доказательство вышеприведенных утверждений, сделанные для сплавов на основе алюминия. Для дополнительной проверки обнаруженных закономерностей мы выполнили аналогичные исследования металлических сплавов на основе золота.
Материалы и методы исследования
Для выявления искомых закономерностей были обработаны данные по 21 системе на основе золота. Основная масса данных была взята из работ [13, 14]. В случае, когда данные были представлены в графическом виде, измеряли тангенс угла наклона прямой на графике состав – свойство. Тангенс угла наклона соответствует коэффициенту b уравнения (1). Если данные были представлены в виде таблицы, то для вычисления коэффициента b использовался разностный метод. Полученные результаты приведены в работе [15]. Далее находили зависимость коэффициентов b от расположения легирующего элемента в периодической системе Д.И. Менделеева.
Результаты исследования и их обсуждение
Рассмотрим поочередно ряд физических свойств, для сплавов на основе золота. Первая величина – твердость по Бринеллю НВ:
HB = HB0 + b1x, (2)
где коэффициент b1 – тангенс угла наклона касательной, x – концентрация легирующего металла. Графики, показывающие зависимость коэффициентов b1 от номера периода N, приведены на рис. 1.
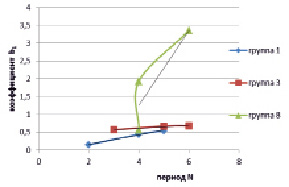
Рис. 1. Зависимость коэффициентов b1 сплавов на основе золота от номера периода N легирующего элемента
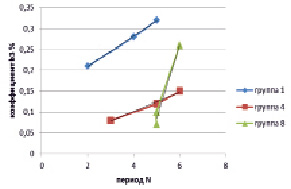
Рис. 2. Зависимость коэффициентов b3 сплавов на основе золота от периода легирующего элемента для различных групп элементов
Анализируя график (рис. 1), мы видим, что для 1, 3 и 8 групп элементов справедливы линейные уравнения, т.е. уравнения вида
b1 = b10 + aN. (3)
Выявленные уравнения приведены в табл. 1.
Таблица 1
Уравнения
|
Номер группы элемента |
b1 = b10+aN |
Достоверность аппроксимации, R2 |
|
1 |
b1 = 0,132 1N – 0,107 9 |
0,992 9 |
|
3 |
b1 = 0,038 6N + 0,460 0 |
0,938 2 |
|
8 |
b1 = 1,052 5N – 2,965 0 |
0,758 9 |
Как видно из приведенных уравнений, наблюдается линейная зависимость между коэффициентами b1 и номером периода легирующего элемента N, что подтверждается высокой достоверностью аппроксимации. На основании полученных уравнений покажем, как можно рассчитать твердость по Бринеллю НВ для неисследованных сплавов на основе золота. Для нахождения коэффициентов, входящих в уравнение (3), использовались данные по металлическим сплавам, содержащим легирующие элементы Li, Cu, Ag (1 группа). Рассчитаем твердость по Бринеллю НВ для Rb. Это элемент 5 периода. После подстановки числа 5 в соответствующее уравнение получаем b1 = 0,552 6 кг/(мм2 вес. %). Далее подставляем полученный результат в уравнение (1). Твердость по Бринеллю чистого золота составляет НВ0 = (24 ± 1,5) кг/мм2. Подставим полученные числа в уравнение (2):
HB = 24 + 0,5526с,
где с – концентрация Rb в вес. %. Например, для сплава на основе золота, содержащего 5 вес. % рубидия, НВ = (26,76 ± 1,5) кг/мм2. Рассмотренный нами пример показывает, как можно вычислять твердость по Бринеллю ранее неисследованных металлических сплавов.
Далее рассмотрим такую физическую характеристику, как твердость по Виккерсу Hn. Для этой величины справедливо уравнение:
Hn = Hn0+b2x, (4)
где коэффициент b2 – тангенс угла наклона касательной.
Значения коэффициентов b2 для элементов 8 группы приведены в табл. 2.
Таблица 2
Значения коэффициентов b2
|
Элемент |
Группа |
Период |
Значение b2, кг/(мм2·вес. %) |
|
Ni |
8 |
4 |
0,3 |
|
Rh |
8 |
5 |
0,21 |
|
Pd |
8 |
5 |
1,78 |
|
Pt |
8 |
6 |
0,68 |
Приведенные данные показывают, что значения коэффициентов b2 испытывают большой разброс и, соответственно, не подчиняются линейной закономерности. Достоверность аппроксимации R2 = 0,07. Если отбросить значение b2 = 1,78 для Pd, считая данное значение выбросом, то мы получим уравнение b2 = 0,19N – 0,5533 с достоверностью аппроксимации R2 = 0,58. Видно, что твердость по Виккерсу Hn испытывает большой разброс значений, поэтому вычислять данную величину для неизученных сплавов нецелесообразно.
Следующая величина, которую мы рассмотрим – это относительное удлинение. Для данной величины были определены коэффициенты b3, входящие в уравнение (5).
δ = δ0 + b3х, (5)
где х – концентрация легирующего металла.
Полученные коэффициенты b3 сведены в табл. 3.
Таблица 3
Значения коэффициента b3
|
Элемент |
Группа |
Период |
Значение b3, % |
|
Li |
1 |
2 |
0,21 |
|
Cu |
1 |
4 |
0,28 |
|
Ag |
1 |
5 |
0,32 |
|
Si |
4 |
3 |
0,08 |
|
Zr |
4 |
5 |
0,12 |
|
Pb |
4 |
6 |
0,15 |
|
Rh |
8 |
5 |
0,10 |
|
Ru |
8 |
5 |
0,07 |
|
Pd |
8 |
5 |
0,48 |
|
Pt |
8 |
6 |
0,26 |
Как видно из табл. 3, коэффициент b3 для палладия выпадает из общей тенденции. Нарушение линейной закономерности связано с особенностью заполнения электронами энергетических уровней. У всех металлов, относящихся к 8 группе, валентные электроны располагаются на S подоболочке. Исключение составляет палладий, валентные электроны которого находятся на d подоболочке. А так как за взаимодействие между атомами в основном отвечают валентные электроны, то свойства сплавов, содержащих Pd, резко отличаются от свойств сплавов с другими легирующими элементами.
Зависимость коэффициентов b3 от номера периода носит линейный характер, что подтверждается высокой достоверностью аппроксимации, приведенной в табл. 4.
Таблица 4
Зависимость коэффициентов b3 от номера периода N
|
Номер группы элемента |
b3 = b30 + aN |
Достоверность аппроксимации, R² |
|
1 |
b3 = 0,036 4N + 0,136 4 |
0,998 8 |
|
4 |
b3 = 0,038 6N + 0,460 0 |
0,988 4 |
|
8 |
b3 = 0,175 0N – 0,790 0 |
0,978 4 |
Следующая величина, рассмотренная нами – это предел текучести σ. Для нее в области твердых растворов, также справедливо линейное уравнение
σ = σ0+b4х, (6)
где х – концентрация легирующего металла, b4 – тангенс угла наклона.
Таблица 5
Значения коэффициентов b4 для различных легирующих металлов в сплавах на основе золота
|
Элемент |
Группа |
Период |
Значение b4, кг/(мм²вес. %) |
|
Li |
1 |
2 |
0,35 |
|
Cu |
1 |
4 |
0,42 |
|
Ag |
1 |
5 |
0,46 |
|
Si |
4 |
3 |
0,22 |
|
Zr |
4 |
5 |
0,26 |
|
Pb |
4 |
6 |
0,30 |
|
Rh |
8 |
5 |
0,25 |
|
Ru |
8 |
5 |
0,22 |
|
Pd |
8 |
5 |
0,65 |
|
Pt |
8 |
6 |
0,41 |
Графики зависимости коэффициентов b4 от периода N для различных групп элементов приведены на рис. 3.
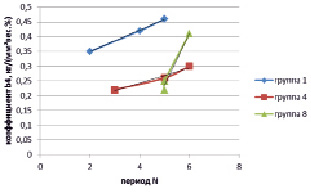
Рис. 3. Зависимость коэффициентов b4 сплавов на основе золота от периода легирующего элемента для различных групп элементов
Как видно из графиков на рис. 3, вновь наблюдается линейная зависимость между коэффициентами b4 (характеризующими предел текучести) и номером периода N легирующих металлов. Соответствующие уравнения приведены в табл. 6.
Таблица 6
Уравнения
|
Номер группы элемента |
b4 = b40 + aN |
Достоверность аппроксимации, R² |
|
1 |
b4 = 0,036 4N + 0,136 4 |
0,998 8 |
|
4 |
b4 = 0,025 7N + 0,140 0 |
0,964 3 |
|
8 |
b4 = 0,175 0N – 0,640 0 |
0,978 4 |
Рассмотренные примеры показывают линейную зависимость между номером периода, к которому относится легирующий металл, и коэффициентами bi (тангенсами угла наклона).
Выводы
1. В ходе работы анализировали влияние 21 легирующего металла на изменения свойств сплавов на основе золота в зависимости от вида легирующих элементов и соответствующего расположения этих элементов в периодической системе Д.И. Менделеева.
2. В данном исследовании был произведен анализ широкого спектра физических характеристик бинарных металлических сплавов на основе золота.
3. Выявлено, что все анализируемые параметры в области твердых растворов изменяются линейно с ростом концентрации легирующего металла.
4. Далее нами были проанализированы коэффициенты, входящие в соответствующие линейные уравнения.
5. Исследования показали, что между коэффициентами, входящими в линейные уравнения, и номером периода N существует линейная взаимосвязь, в случае принадлежности легирующих металлов к одной группе.
6. Основываясь на выявленных закономерностях, мы можем теоретически предсказать свойства еще не изученных сплавов, не прибегая к эксперименту, что позволяет экономить материальные и финансовые ресурсы.
7. В статье приведен пример расчета твердости по Бринеллю сплава Au–Rb, с использованием данных по величинам твердости сплавов Au–Li, Au–Cu, Au–Ag.
Библиографическая ссылка
Леонов В.В., Никифоров А.Г., Ковалева А.А., Эльберг М.С., Черняк М.Ю. ВЗАИМОСВЯЗЬ МЕЖДУ ФИЗИЧЕСКИМИ ХАРАКТЕРИСТИКАМИ СПЛАВОВ НА ОСНОВЕ ЗОЛОТА И ПОЛОЖЕНИЕМ ЛЕГИРУЮЩИХ ЭЛЕМЕНТОВ В ТАБЛИЦЕ Д.И. МЕНДЕЛЕЕВА // Международный журнал прикладных и фундаментальных исследований. 2018. № 7. С. 26-31;URL: https://applied-research.ru/ru/article/view?id=12324 (дата обращения: 06.01.2026).

