Известно, что для всех направлений медицинских исследований, как прикладного так и фундаментального характера, моделирование гемодинамических, физико-механических и электрофизических характеристик биологических объектов является неотъемлемым [1]. При этом развитие моделирования применительно к спортивной медицине во многом связано и зависит от аппаратно-приборной базы существующих систем и методов диагностики, внедрение которых позволило значительно облегчить диагностику патологий сердца и сердечно-сосудистой системы на ранних этапах [2, 3].
На текущий момент разработано достаточно большое количество моделей сердца и сердечно-сосудистой системы (ССС). Из них в медицинской практике, в силу высокого уровня визуализации исследуемых структур, как правило, применяются геометрические и физические модели ССС [4, 5], однако вследствие большого количества возможных состояний, вызванных как морфологическими так и функциональными особенностями, подобные модели не позволяют учесть накопленный к настоящему времени обширный экспериментальный материал. Больший интерес представляют модели, позволяющие описать существенные для оригинального объекта факторы и параметры. Такие модели биологических объектов предполагают наличие трех основных подклассов, а именно гемодинамические, кинетические и электрические математические модели. Однако классические математические модели, описывающие происходящие в ССС процессы, имеют ограниченное практическое применение, так как теоретические предпосылки основываются на постулате об однородности миокарда и ограничены построением упрощенных моделей, не учитывающих физиологическое и патофизиологическое влияние феномена топологии миокарда. В то же время в работе [5, 6] излагалось теоретическое описание CCC и формулировалась задача о математическом моделировании ССС, основанной на недавнем открытии ученых [4] показавшем, что миокард сердца имеет топологию Мебиуса. При этом утверждается, что построение математической модели, воспроизводящей основные функции ССС с учетом такой анатомии миокарда, обеспечивает физиологически реальные, близкие к результатам клинических наблюдений, характеристики гемодинамики, физико-механики и электрофизики ССС.
Цель исследования: анализ существующих в настоящее время моделей работы сердца и сердечно-сосудистой системы, сложившихся в ходе становления существующих систем и методов диагностики патологий, основанных на постулате об однородности миокарда.
Материалы и методы исследования
В работе на основании практического подхода к исследованию электрической и механической функций в сравнении однородного и неоднородного миокарда сердца выполнен анализ существующих математических моделей, описывающих работу ССС. Отличительной особенностью такого подхода является возможность выявления, в приближении миокарда как объекта с топологией Мебиуса, необходимости учета физиологической и патофизиологической значимости неоднородности миокарда.
Результаты исследования и их обсуждение
Одной из наиболее известных в настоящее время моделей ССС является гемодинамическая модель [7, 8]. Рассмотрим особенности моделирования ССС в рамках концепции «миокард новой топологии». Известно [9], что математическое описание течения кровотока основано на использовании системы уравнений, в которой формальная запись общего вида на каждом ребре графа имеет вид
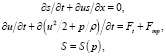(1)
где S – площадь поперечного сечения кровеносного сосуда; u – линейная скорость движения крови; р – давление крови;
t – время; x – длина, вдоль оси каждого сосуда; ρ – плотность крови ρ = const; Ft – внешняя сила, например, земного притяжения;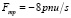 
– сила вязкого трения потока крови о стенки сосуда; n – коэффициент вязкости крови.
Из системы уравнений гемодинамики (1), состоящей из нелинейных дифференциальных и алгебраических уравнений, видно, что наиболее удобным способом ее решения является численный метод. В настоящее время для реализации численных методов решения систем дифференциальных уравнений удобно использовать пакеты прикладных программ математического моделирования объектов, например пакеты аппаратного обеспечения вычислительных систем типа АNSIS, NASTRAN/PATRAN, ELCUT и т.д. Следует отметить, что перечисленные пакеты аппаратного обеспечения позволяют так же рассчитывать, например, неньютоновские биологические жидкости, такие как кровь, учитывать анизотропнность среды, в частности физико-механические свойства миокарда, характеристики электромагнитопроводящих сред для учета электрофизических свойств миокарда. Применительно для обеспечения работы высокоперспективного медоборудования, такого как, например, многофункциональный ультразвуковой аппарат для проведения сердечно-сосудистых исследований, а также других медицинских приборов предполагающих использование микро- и нано- электромеханических устройств, применение пакетов аппаратного обеспечения типа АNSIS, NASTRAN/PATRAN, ELCUT делает многообещающим разработку и дальнейшее усложнение теоретической модели и системы уравнений (1), описывающих гемодинамические процессы. Однако видно, что математическая модель (1) не позволяет учесть изменение кинетической вязкости крови во время сердечного цикла, а также различность и неодинаковость в режимах течения крови в том числе, например, cпурт-эффект течения неньютоновской жидкости. Таким образом, модель гемодинамики в настоящее время не может быть использована для решения задач, связанных с оптимизацией режима течения крови в ССС. Для решения задач оптимизации в систему уравнений гемодинамики необходимо дополнительно включить учет гидромеханических свойств и особенностей ССС. В этом случае описание режима течения крови, например, на основе программ ANSIS и NASTRAN/PATRAN потребует создания вычислительного комплекса, описывающего гемодинамику ССС в рамках концепции «миокарда новой топологии» в виде 3D-конечноразностной сетки русла кровотока сердца. Следует отметить, что создание программой модели гемодинамики ССС возможно на основе информации, получаемой с помощью современных комплексов ультразвуковой диагностики. Это позволит улучшить механизм работы электронных датчиков и других составляющих диагностического оборудования, что дает основания полагать, что созданная модель изменит основополагающие представления в данной области.
Другой известной и не менее распространенной в настоящее время классической теоретической моделью, описывающей деятельность ССС, является кинетическая модель [10, 11], математический аппарат которой рассматривает сердце как некий однородный объект, который создает давление и сообщает крови кинетическую энергию [12]. Рассмотрим особенности теоретической основы кинетической модели. Известно, что основным параметром моделирования в такой физико-механической модели является сердечный ритм, тогда в интервале одного сокращения работа любого из желудочков сердца может быть определена из выражения
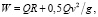(2)
где Q – выброс крови из желудочка; R – сопротивление кровотоку; g – ускорение свободного падения.
Видно, что в кинетической модели (2) работа сердца за одно сердечное сокращение в общем случае зависит не только от переноса некоторого количества крови в артериях, а также связана с формированием упругого напряжения в сердечной мышце. В рамках концепции «миокард новой топологии» это делает актуальным разработку функциональной модели сердца, описывающей физико-механические процессы для многочастотных широкополосных электронных датчиков при формировании луча на прием/передачу в многофункциональных диагностических медицинских аппаратах для проведения ультразвуковых исследований ССС.
Как было показано выше, одно из новых направлений в моделировании процессов и построении имитационной модели работы ССС основано на представлении миокарда сердца как фигуры с топологией Мебиуса [13]. Учет критически значимых качественных свойств и особенностей миокарда сердца в описании работы ССС позволяет рассмотреть миокард как комбинацию сочетания набора магнитных доменов, что в свою очередь позволяет связывать биомеханику сокращений мышц сердца и гемодинамику течения крови в эластичных сосудах в тесном взаимодействии с электропроводящими процессами, обеспечивающими регулирование ССС в целом:
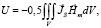(3)
где V – объем магнетика; JS – намагниченность; Hm – напряженность магнитного поля.
Представления о строении миокарда в виде листа, свернутого в соответствии с топологией Мебиуса, ставят вопрос о дальнейшем изучении влияния связанности и ориентированности всей кровеносной системы и ее сопряжения с сердцем, поскольку Мебиусово трансформирование представляет из себя композицию конечного числа инверсий относительно сфер в евклидовом пространстве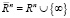 
. Причем множество всех Мебиусных преобразований пространства 
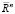конечномерно, а его подгруппа, составленная из отображений, сохраняющих ориентацию, изоморфна 
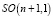[14]. Изоморфность подгруппы, составленной из отображений, представляет особую важность при математическом моделировании в рамках трансформаторной модели сердца, согласно которой распространение магнитного поля, создаваемого миокардом сердца, описывается в приближении, согласно которому миокард сердца представлен как магнитопровод, образуемый материалами с ориентированной доменной структурой. Действительно, из (3) видно, что для пространства, заполненного магнитным материалом с намагниченностью JS магнитостатическое взаимодействие обособленных элементов объема внутри намагниченного тела приводит к наличию собственной магнитостатической энергии этого тела, и величина поля рассеяния Hm ведет к образованию областей спонтанного намагничивания, т.е. доменной структуры. Это позволяет считать миокард сердца за магнитную доменную структуру – совокупность областей в магнитной подсистеме магнитных материалов, которые связывают микроскопические магнитные характеристики с их макроскопическими свойствами. Таким образом, при математическом описании процессов формирования в миокарде магнитного поля принимаем, что намагничивание и перемагничивание определяется свойствами доменной структуры.
При трансформации топологии магнитопровода, в частности его изменение из торроидальной формы в форму в виде петли Мебиуса, наблюдается изменение напряженности магнитного поля, вызванное влиянием изменения ориентации доменов. Это позволяет, по результатам анализа напряженности магнитного поля, решить задачу «визуализации» внутренней структуры миокарда сердца, так как амплитудные значения напряженности магнитного поля различаются для нормального (скрученного миокарда) и патологий на величину до 2 раз. Достоверность сделанных предположений (3) качественно подтверждается как результатами физического эксперимента, проводимого в формате клинических наблюдений [15], так и результатами вычислительного эксперимента [13].
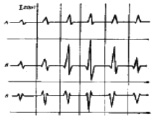
Усредненные показатели QRS комплекса МКГ здоровых людей (А) с гипертрофией левого желудочка (Б) и с инфарктом миокарда (В) [15]
Новый подход к моделированию CCC человека, позволяет связать воедино электро-биомеханические процессы что дает возможность ранней диагностики развития патологий на основе оценки изменения характеристик функционирования CCC. В этом случае модель CCC может быть представлена в виде 3D-конечноэлементной модели, описывающей физико-механические процессы, происходящие в сердце, включающей комплекс, базирующийся на изучения и доказательстве результатов следующих гипотез: спиральная мода колебаний – значимая характеристика здорового сердца (это основа для ранней диагностики патологий); энергетика здорового сердца в 4 раза меньше, чем энергетика больного сердца (конфигурация цилиндрического кольца основа для прогнозирования омертвения волокон миокарда); мышечная стимуляция миокарда распространяется в виде уединенной волны «сжатия – растяжения».
Заключение
Выполненный анализ существующих в настоящее время моделей работы сердца и сердечно-сосудистой системы, сложившихся в ходе становления существующих систем и методов диагностики патологий, основанных на постулате об однородности миокарда, показал интерес к ревизии и дальнейшему развитию классических теорий, используемых для описания электро-, био-, механических процессов в сердечно-сосудистой системе. Принимая во внимание тот факт, что физиологическая и патофизиологическая значимость феномена топологии миокарда изучена в настоящее время недостаточно полно, существует высокая потребность в системно-синергетическом подходе к принципиальному переосмыслению и пересмотру существующих математических моделей, описывающих работу сердца и сердечно-сосудистой системы с точки зрения учета новых, критически значимых качественных свойств и особенностей миокарда сердца.
Применение системно-синергетического похода к моделированию ССС, учитывающего синхронизацию между различными процессами, формирующими электро-биомеханику функционирования ССС, позволит в большей степени обеспечить соответствие локальных и нелокальных характеристик результатам физиологических экспериментов и клинических наблюдений. Это будет способствовать росту эффективности и ускорит адаптацию новых средств моделирования в клинических приложениях, как для диагностики сердечной деятельности, так и для разработки электромеханических стимуляторов ССС и целевых тренажеров для кардиохирургов, что позволит увеличить надежность и повысить вероятность эффективного проведения хирургических операций на ССС.
Библиографическая ссылка
Арутюнов Ю.А., Чащин Е.А., Шашок П.А. ПРОГРАММНОЕ МОДЕЛИРОВАНИЕ СЕРДЕЧНО-СОСУДИСТОЙ СИСТЕМЫ ДЛЯ ИССЛЕДОВАНИЯ ГЕМОДИНАМИЧЕСКИХ, ФИЗИКО-МЕХАНИЧЕСКИХ И ЭЛЕКТРОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК МИОКАРДА НОВОЙ ТОПОЛОГИИ // Международный журнал прикладных и фундаментальных исследований. – 2018. – № 10. – С. 54-58;URL: https://applied-research.ru/ru/article/view?id=12416 (дата обращения: 19.04.2024).