В настоящее время в школьном образовании по естественнонаучным дисциплинам остро ощущается то, что школьники не умеют решать задачи. Анализируя популярные существующие методы решения задач, было выявлено, что каждый из них не покрывает всех потребностей школьников. Многие методы, такие как аналитико-синтетический метод [1], метод исчерпывающих проб, алгебраический метод, метод сведения к ранее решенным задачам, графический метод и другие, основываются на том, что школьникам нужно «увидеть» решение. Но не все ученики способны сразу сообразить, какой метод решения надо применять в той или иной задаче. Поэтому необходим универсальный метод, который приведет к решению любой задачи.
Авторами была разработана и описана технология решения задач методом табличного анализа [2], которая позволяет устранить пробелы других популярных методов. Однако для того, чтобы решить задачу методом табличного анализа, ученик должен хорошо представлять себе явление, о котором идет речь в задаче, определить закон, описывающий это явление. Но что делать, если законов несколько или явление в тексте задачи кажется таким запутанным, что трудно выявить участников? Для этого случая автором была разработана и представлена в данной статье технология решения задач методом физического анализа, которая позволяет на первом этапе анализа условия задачи выявить как всех участников, так и необходимые законы, а затем приступать к решению задачи.
Ранее в статье «Технология решения задач методом табличного анализа» нами уже был разработан один универсальный метод решения текстовых задач. Однако он имеет ограничение: для того, чтобы применять технологию решения задач методом табличного анализа, необходимо знать закон, на который дана задача. Целью данной работы является разработка такого метода решения задач, с помощью которого можно бы было преодолеть затруднения, которые могут возникать на начальной стадии табличного анализа, чтобы потом решить задачу либо методом физического, либо табличного анализа. В данной работе будет разработан подход, который устранит данное ограничение табличного анализа и позволит приступить к решению задачи, даже если закон нам еще не понятен.
Материалы и методы исследования
Универсальный подход, который будет разработан в данной работе, будет иметь название «Технология решения задач методом физического анализа». Данная технология устраняет недостатки метода табличного анализа задачи, для которого требуется сразу после прочтения условия задачи точное определение закона, на который дана задача, а также ее участников и их взаимосвязей друг с другом.
Под «участниками» понимаются объекты, имеющие определенные характеристики, которые взаимодействуют по определенным правилам – законам.
Слово «технология» в данном контексте подразумевает алгоритм, следуя которому задача будет обязательно решена. В частности это относится к задачам уровня средней школы, которые имеют однозначное решение.
Результаты исследования и их обсуждение
Технология решения задач методом физического анализа основана на построении схем для визуализации процессов происходящих в задаче. Схема позволяет понять, как взаимодействуют все объекты задачи. Физический анализ помогает определить закон, на который дана задача. Технологию можно представить в виде 10 этапов:
Этап 1. Внимательно прочитать условия. На первом этапе необходимо разобраться в условиях задачи. Необходимо убедиться, что каждое слово понятно. Если встречаем незнакомое слово в тексте задачи, то прежде чем приступать к решению, обязательно выясняем значение этого слова, так как оно может существенно менять смысл задачи.
Этап 2. Составление «Дано». После прочтения условий задачи необходимо сделать формализованную запись этих условий. Составляется раздел «Дано». В этот раздел («Дано») необходимо занести численные значения всех известных величин из условий задачи. Лучше сразу перевести все заданные значения в одинаковые размерности. Также необходимо указать все скрытые данные, явно не указанные в задаче, но которые можно взять из справочника. Например, в задаче на свободное падение тел необходимо знать ускорение свободного падения, хотя в задаче об этом ничего не сказано. Ученику было бы легче, если бы в «Дано» сразу было отмечено, что ускорение свободного падения взять, например, 10 м/c2. А главное, в «Дано» надо обозначить искомую величину, которую необходимо найти по условиям задачи. Это позволит всегда помнить о цели решения задачи, а также о том, в какой размерности должен быт ответ.
Этап 3. Анализ задачи – составление схемы. Важный этап для решения задачи методом физического анализа – это составление схемы. Именно на этом этапе приступаем к физическому анализу задачи. Под физическим анализом понимаем составление схемы или рисунка, на котором изображено то явление, о котором идет речь в задаче. Схема должна быть такой, чтобы на ней хорошо были видны все характеристики явления. Все буквенные данные должны присутствовать на рисунке. В геометрии всегда применяют физический анализ. Также физический анализ распространен в задачах по физике.
Необходимо отметить, что если ученик не понимает само явление, о котором идет речь в задаче, и не знает законов, описывающих это явление, то это означает, что ученику еще рано решать данную задачу. Вместо решения задачи он должен сначала изучить данное явление, а потом уже применять метод физического или табличного анализа [2].
Этапы 2 и 3 лучше выполнить параллельно. Для того чтобы проверить, насколько качественно выполнены первые три этапа, проверьте, можете ли вы отложить учебник с условиями задачи. Если больше не возникает потребности заглянуть в текст, значит, первые этапы выполнены качественно.
Этап 4. Запись законов. Решение должно начаться с записи законов (формул), в которые входит искомая величина. В физике каждая величина обозначается своей буквой, в математике неизвестные обозначаются буквами «x», «y», «z»…и т.д. Закон необходимо выписывать с учетом тех обозначений, которые использовали в разделе «Дано» и на схемах.
Этап 5. Промежуточные искомые. Выражаем искомую величину из закона и смотрим: каких величин не хватает в «Дано», чтобы ее найти. Эти величины становятся «промежуточными искомыми». Необходимо выписать промежуточные искомые.
Этап 6. Законы для «промежуточных искомых». Повторяем этап 4 для «промежуточных искомых»: выписываем законы (формулы) для «промежуточных искомых величин» и выражаем их.
Этапы 5 и 6 необходимо повторять до тех пор, пока не выразятся все «промежуточные искомые величины». Отметим, что из одного закона в одной ситуации нельзя найти две величины. Поэтому, если закон уже использовался для нахождения одной величины в данной ситуации, то для нахождения другой величины надо использовать другие законы, либо другие ситуации задачи, где еще фигурирует «промежуточная искомая величина». Под «другими ситуациями» мы понимаем те же объекты, но находящиеся в изменившихся отношениях между собой по каким-либо причинам из условий задачи. Должны прийти к тому, что все величины выражены через известные величины и через искомую величину, либо предыдущую «промежуточную искомую величину».
Этап 7. Подставляем «промежуточные искомые». Подставляем «промежуточные искомые величины» в соответствующие формулы, для которых их искали. Подставляем вплоть до первой формулы с искомой величиной. Если «промежуточные искомые величины» выражались через предыдущие искомые, то получаем уравнение относительно искомой величины. Иногда вместо одного уравнения можем получить систему нескольких уравнений.
Этап 8. Выражаем искомую величину из конечного уравнения. Решаем уравнение относительно искомой величины согласно технологии решения уравнений (или системы уравнений). Находим искомую величину в общем виде.
Этап 9. Находим значение искомой величины. Перед расчетом рекомендуем проверить, что вы верно выделили искомую величину. Для этого в конечное уравнение подставляем размерности всех задействованных в уравнении значений и выполняем с ними те же математические действия. В результате должна получиться размерность как у искомой величины в условиях задачи. Если размерность совпала, то переходим к выполнению математических операций с числами.
Подставляем в общее решение численные значения. Все значения должны быть с единицами измерения. Если вы не проверили отдельно размерность, то можете сразу при расчете численных значений выполнять те же действия с их единицами измерений. Если в результате всех расчетов размерность получилась такая, какая должна быть у искомой величины, и все расчеты были проведены верно, значит задача решена.
Этап 10. Записываем ответ. Помните, что в ответе задачи важно указать не только численное значение, но и размерность.
После того, как мы разобрали каждый этап, предлагаем применить их на практике и разобрать пример решения задачи с использованием технологии решения задач методом физического анализа.
Для разбора примера возьмем не сложную задачу, но хорошо иллюстрирующую все этапы технологии. Задача:
На речном трамвайчике можно совершить трехчасовую прогулку до поворота реки и обратно. Скорость течения реки 2 км/ч. Собственная скорость трамвайчика 15 км/ч. Какова длина прогулочного маршрута?
Этап 1. Внимательно прочитать условия. Читаем условие.
Этап 2. Составление «Дано». Выписываем все известные значения из условий задачи и указываем искомую величину – длина всего маршрута l.
Этап 3. Анализ задачи – составление схемы. Выполним физический анализ и составим схему движения трамвайчика по реке. Подпишем переменные. Схема позволяет увидеть, что данная задача на закон движения по реке (по течению и против течения). Схема представлена на рисунке.
На рисунке представлены «Дано» и схема явления после выполнения этапов 2 и 3.
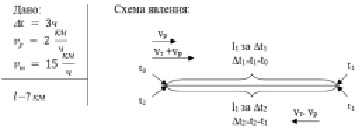
«Дано» задачи и схема явления, о котором говорится в задаче
Этап 4. Запись законов.
Закон для нахождения искомой величины L – общий закон, согласно которому общий путь равен сумме путей на отдельных участках, из которых состоит путь: L = L1 + L2. Подставим обозначения из схемы и получим закон относительно нашей задачи:
L = L1 + L1 = 2*L1. (1)
Этап 5. Промежуточные искомые. Так как значение величины L1 нам не известно из «Дано», она становится промежуточной искомой: L1 = ? км.
Этап 6. Законы для «промежуточных искомых».
6.1. Выражаем промежуточную искомую L1.
Закон для нахождения промежуточной искомой величины L1 – общий закон скорости V = L/∆t на первом участке, где трамвайчик идет по течению реки:
L1 = (Vт + Vр)*∆t1. (2)
6.2. Выражаем промежуточную искомую ∆t1.
Величина ∆t1 не известна из «Дано». Теперь она становится промежуточной искомой: ∆t1 – ? ч. Эта величина фигурирует в задаче на первом участке движения (по течению реки), но мы не можем использовать закон скорости, так как из него на этом участке мы нашли величину L1.
Закон для нахождения промежуточной искомой величины ∆t1 – общий закон, который получился у нас в анализе (на схеме), согласно которому общее время движения равно сумме интервалов времени на отдельных участках, из которых состоит путь: ∆t = ∆t1 + ∆t2. Выразим ∆t1:
∆t1 = ∆t – ∆t2. (3)
6.3. Выражаем промежуточную искомую ∆t2.
Величина ∆t2 не известна из «Дано». Она тоже становится промежуточной искомой, ∆t2 = ? ч.
Закон для нахождения промежуточной искомой величины ∆t2 – общий закон скорости V = L/∆t на втором участке, где трамвайчик идет против течения реки: L1 = (Vт – Vр)*∆t2. Выразим ∆t2:
∆t2 = L1/(Vт – Vр). (4)
Этап 7. Подставляем «промежуточные искомые».
Выразим ∆t1:
∆t1 = ∆t – L1/(Vт – Vр). (5)
А затем найдем L1:
L1 = (Vт + Vр)*(∆t – L1/(Vт – Vр)). (6)
Этап 8. Выражаем искомую величину из конечного уравнения.
Из уравнения, полученного на 7 этапе, выражаем L1:
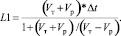(7)
Подставляем промежуточную искомую величину L1 в формулу для искомой величины L:
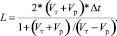(8)
Получили конечное уравнение.
Этап 9. Находим значение искомой величины.
В конечное уравнение подставляем численные значения из «Дано»:
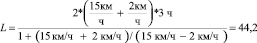км. (9)
Этап 10. Записываем ответ.
Ответ: Длина всего прогулочного маршрута равна 44,2 км.
Задача решена.
Заключение
Таким образом, была разработана и применена на практике технология решения задач методом физического анализа. Данная технология является универсальным методом, который позволяет решать любые текстовые задачи, включая задачи по геометрии и задачи на комбинацию различных законов, что трудно сделать методом табличного анализа.
Технология решения задач методом физического анализа является более распространенной и интуитивно понятной схемой решения задач. На практике большинство задач так или иначе решаются с помощью физического анализа. В данной статье был формализован и описан метод решения задач с помощью физического анализа в том виде, который позволяет решать задачи максимально эффективно.
Более того, разобранная технология может являться дополнением технологии табличного анализа: с помощью физического анализа определяем участников задачи, характеристики участников и законы, связывающие их, а затем переходим к решению задачи с помощью табличного анализа. В задачах со многими законами, после применения схем физического анализа с выявлением всех характеристик участников, возможно поэтапное решение задачи с помощью табличного анализа по каждому закону. Для этого в ходе решения задачи составляется несколько таблиц, связанных использованием результатов друг друга. В такой комбинации применения технологий физического и табличного анализа, мы, с помощью физического анализа, гарантированно разбираемся с явлениями и законами, необходимыми для решения задачи, а с помощью использования табличного анализа быстрее составляем уравнения и делаем вычисления.
В результате, технологии физического и табличного анализа задач дополняют друг друга, позволяя решить главную методическую задачу обучения школьников математике – разработать полный комплекс методик решения текстовых задач, который позволяет решать любые задачи школьного курса, включая задачи по физике и геометрии. Так как данные технологии доказали свою целесообразность, именно они используются для разбора задач на занятиях, проводимых преподавателями Сетевой инженерно-технической школы СИТШ [3, 4], а также с помощью данных технологий будут организовываться онлайн-курсы для организации дистанционного обучения с помощью Систем дистанционного обучения [5].
Библиографическая ссылка
Дубинин Н.Н., Назарова Ю.Ю. ТЕХНОЛОГИЯ РЕШЕНИЯ ЗАДАЧ МЕТОДОМ ФИЗИЧЕСКОГО АНАЛИЗА // Международный журнал прикладных и фундаментальных исследований. – 2018. – № 12-1. – С. 125-129;URL: https://applied-research.ru/ru/article/view?id=12534 (дата обращения: 16.04.2024).