На территории Кыргызстана грузы перевозятся по горным дорогам. Автомагистраль «Бишкек – Ош» играет важную роль в экономике Кыргызстана. Она соединяет столицу – Бишкек с южными областями страны и соседними республиками – Узбекистаном, Таджикистаном и Казахстаном. Дорога проходит через перевал Тоо-Ашуу, дорожные условия считаются высокогорными, следовательно, сложными. В связи с тем, что железнодорожное сообщение с южными областями проходит через территорию другой республики, водного сообщения нет, количество транспортных средств, перевозящих грузы по этой дороге, значительно.
Вследствие всплескивания жидких грузов в процессе транспортировки изменяются координаты центра тяжести груженых транспортных средств, что изменяет величину максимальной скорости движения. Установление оптимальных значений скоростного режима определит безопасность перевозки грузов грузовыми транспортными средствами [1–3].
В связи с тем, что условия эксплуатации транспортных средств очень тяжелые, необходимо разработать методику расчета процесса движения транспортных средств с жидким грузом при изменении величины радиуса закругления, при значительном количестве подъемов, спусков, поворотов и серпантинов. Актуальность вопроса растет при транспортировке жидких грузов, особенно в условиях отсутствия других видов сообщений.
Цель исследования: разработка методики расчета процесса движения автопоезда с жидким грузом при изменении величины радиуса закругления, скорости и ускорения и координат центра тяжести груженых транспортных средств, установление силы воздействия на внутренние поверхности цистерны и разделительные стенки во время движения на поворотах различного радиуса закругления.
Разработка методики расчета процесса движения автопоезда с жидким грузом с учетом изменения таких параметров, как радиус поворота, скорость, ускорение грузового автомобиля и смещение центра его тяжести за счет движения жидкости, даст возможность установить оптимальные значения скоростного режима грузовых транспортных средств, перевозящих жидкие грузы, для конкретных дорожных условий.
Изучалось влияние на движение транспортных средств с жидким грузом скорости передвижения грузовых транспортных средств, с учетом продольного и поперечного уклонов поверхности дороги, а также кинетического воздействия жидкого груза на внутренние поверхности и разделительные стенки цистерны.
Определение оптимальных значений скоростного режима позволит повысить эффективность транспортировки жидких грузов грузовыми транспортными средствами. Разработана методика с установлением максимальных значений скоростного режима, при которых обеспечиваются условия устойчивости и безопасности движения. В методике была применена математическая модель движения автомобиля, решаемая обратными задачами раздела физики – динамикой транспортных средств, позволяющих установить параметры движения при изменении координат центра тяжести груженого транспортного средства.
Доля движения по дорогам с изменением величины радиуса закругления при передвижении грузовых транспортных средств по горным дорогам значительна. Величины радиуса закругления составляют от 20 м до 500 м. Особенности движения грузовых транспортных средств по дорогам с изменением величины радиуса закругления зависят от оптимальных значений скоростного режима.
Обеспечение оптимальных значений скоростного режима диктуется необходимостью достаточно высоких показателей эффективности и безопасности движения транспортных средств с жидким грузом на горных дорогах, с учетом особенностей действия сил сцепления колес с дорогой на этих дорогах. В противном случае, при максимальных скоростях, определенных значениях продольного и поперечного уклонов поверхности дороги, а также дополнительного увеличения сил опрокидывания могут быть нарушены условия устойчивости (сопротивляемости) опрокидыванию или заносу.
Максимальные значения скорости движения транспортных средств на горных дорогах могут снижаться, если количество осей больше обычно используемых. На максимальные значения скорости движения транспортных средств оказывают также влияние продольная и боковая реакции, перегруз транспортных средств, что увеличивает их силы инерции.
Обеспечение высокой эффективности эксплуатации транспортных средств в рассматриваемых условиях предполагает установление показателей эффективности и безопасности режима движения данного автомобильного транспорта на этих дорогах.
Для описания режима движения транспортных средств требуется составить систему уравнений сил и моментов, обеспечивая выполнение требований устойчивости. Режим движения зависит от квалификации и психофизиологического состояния (утомляемости и остроты реакции) водителя, от конструкции органов управления и их технического состояния, от условий видимости (метеорологических условий), типа и состояния покрытия (сухое, оледенелое), от ширины и формы проездов и интенсивности движения. Отсюда видно, что мы имеем типичный пример стохастических, статистических связей, требующих вероятностно-статистического подхода к оценкам режимов движения [4–6].
При проведении исследований грузовые транспортные средства рассматривались как система, которая состоит из двух элементов – тягача и полуприцепа (рис. 1).
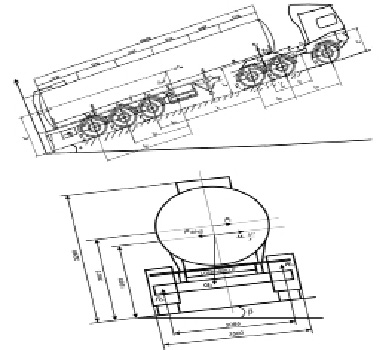
Рис. 1. Геометрические размеры, схема действующих сил тягача и полуприцепа
После проведения интегрирования нами была получена система, состоящая из двадцати восьми уравнений. Данная система с учетом начальных и граничных условий является математической моделью и описывает особенности режимов движения грузовых транспортных средств в горных условиях эксплуатации [2, 4].
Силы воздействия на внутренние поверхности цистерны и разделительные стенки рассчитывались уравнением Навье – Стокса в цилиндрических координатах (г, е, z) с применением программного комплекса SolidWorks + Cosmos.
На рис. 2 представлена схема периодического воздействия на внутренние поверхности цистерны и разделительные стенки с указанием скорости перемещения жидкости.
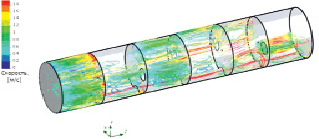
Рис. 2. Схема периодического воздействия на внутренние поверхности цистерны и разделительные стенки с указанием скорости перемещения жидкости
На рис. 3 даны результаты расчета сил воздействия на внутренние поверхности цистерны и разделительные стенки во время движения на поворотах различного радиуса закругления, а также изменение этих величин при различных скоростях движения автопоезда.
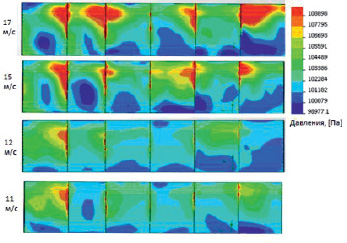
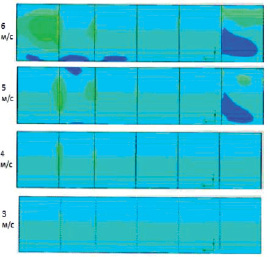
Рис. 3. Изменение сил воздействия на внутренние поверхности цистерны и разделительные стенки во время движения на поворотах различного радиуса закругления
Предложенная модель позволяет определить граничные значения скорости движения транспортных средств с учетом влияния радиусов закругления поворотов, продольного и поперечного уклонов поверхности дороги, скорости и ускорения для широкого диапазона условий эксплуатации.
Результаты расчета сил по условиям устойчивости (сопротивляемости) опрокидыванию или заносу для определенного диапазона значений скорости движения автопоезда, с учетом добавочного воздействия жидкого груза на внутренние поверхности цистерны и разделительные стенки цистерны (рис. 4 и 5).
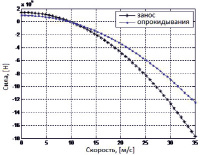
Рис. 4. График сил по условиям устойчивости (сопротивляемости) опрокидыванию или заносу для определенного диапазона значений скорости движения автопоезда, с учетом дополнительного увеличения сил опрокидывания, за счет добавления кинетического воздействия жидкого груза на внутренние поверхности цистерны и разделительные стенки цистерны (радиус закругления дороги R = 50 м и продольный уклон дороги – 3 %)
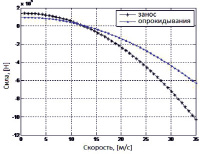
Рис. 5. График сил по условиям устойчивости (сопротивляемости) опрокидыванию или заносу для определенного диапазона значений скорости движения автопоезда, с учетом дополнительного увеличения сил опрокидывания, за счет добавления кинетического воздействия жидкого груза на внутренние поверхности цистерны и разделительные стенки цистерны (радиус закругления дороги R = 100 м и продольный уклон дороги – 7 %)
Выводы
На вышеприведенных графиках видны особенности изменения сил по условиям устойчивости (сопротивляемости) опрокидыванию или заносу для определенного диапазона значений скорости движения автопоезда. Используя указанные графики, можно определить граничные значения скорости, при которой нарушаются условия устойчивости и безопасности движения транспортных средств.
Библиографическая ссылка
Давлятов У.Р., Алымкулов А.Ш., Омуров Ж.М. МЕТОДИКА РАСЧЕТА ПРОЦЕССА ДВИЖЕНИЯ СЕДЕЛЬНОГО АВТОПОЕЗДА С УЧЕТОМ ДИНАМИЧЕСКОГО ВОЗДЕЙСТВИЯ ЖИДКОГО ГРУЗА НА СТЕНКИ ЦИСТЕРНЫ // Международный журнал прикладных и фундаментальных исследований. 2019. № 4. С. 25-29;URL: https://applied-research.ru/ru/article/view?id=12691 (дата обращения: 13.03.2026).

